前言
我在算法学习过程中,针对斐波那契数列模型的动态规划的例题进行了一个整理,并且根据标准且可靠一点的动态规划解题思路进行求解类似的动归问题,来达到学习和今后复习的必要。
所谓的斐波那契数列模型,即当前状态的值等于前两种状态的值之和。下面的例题的动态规划递推式都是类似的形式。

一、动态规划解题流程
针对于动态规划类似的题目,一般有如下的解题套路:
1.确定状态表示
通常状态我们可以理解为dp表中的每一个值。
此时就跟经验和题目要求相关了。在一维的线性递推模式下(一维数组),一般经验有dp[i]的第i个表示:
1.从第i个开始....
2.到第i个结束...
... 省略的根据题目情况而定,而一般定下的也和我们返回的结果有关。
比如求解上楼梯的方式问题,dp[i]可以表示上第i阶楼梯时有多少种方式(到第i个结束);或者从第i阶楼梯上到顶层楼梯有多少种方式(从第i个开始)。
实际上,也需要我们在分析问题的过程中,发现重复子问题的过程。
2.建立状态转移方程
这一步是核心的一步也是最难的一步。
动态规划基本上解题是基于dp表的,那么对dp表中的状态赋值需要靠建立的转移方程求解。对此一般存在一个基本的思想:dp[i] 的值可以由最近的值如何求解出来?根据题目上的条件。
一般的经验也是以i位置的状态,最近的一步划分问题。
3.初始化
一般状态转移方程中存在让dp表越界的机会,初始化就是为了防止填dp表越界。
基本上完成上面1、2步后,接下来的几步就非常简单了。
4.填表顺序
根据状态转移方程,存在一定的填表顺序,比如斐波那契数列模型,我们每次求当前值时需要知道前面两个值,所以需要从左向右进行赋值。
根据题目和状态定义,灵活的调整填表顺序。
5.返回值
一般返回值就是题目最终要的结果,通常就是返回dp表中的某个状态值。
二、例题1-第n个泰波那契数
在我的上一篇博客中详细提过~
【算法学习】第N个泰波那契数-CSDN博客
三、例题2-三步问题
题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
解析题目:
根据动态规划解题思路,我们首先需要确定状态表示。
我们想要求对应台阶小孩有多少种上楼梯的方式,实际上就是经验所谈的到第i结束...。而这里的... 就是题目中的上楼梯的多少种方式,所以这里可以得到状态表示为:
dp[i] = 小孩上第i阶台阶方式总数。
然后我们需要确定状态转移方程。
结合我们之前说过的,从对应值的身边最近状态入手,在结合题目思路就可以得出结果了:因为小孩一次可以上1阶、2阶、3阶。那么dp[i] 此时第i阶台阶可以是通过1阶、2阶、3阶上来的。那么可以存在如下的关系:

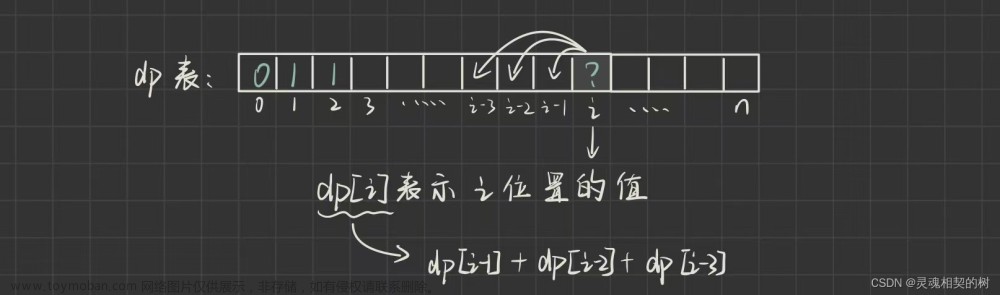
而这实际上对应着如下的关系:
状态转移方程:(i > 3)
dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3]
因为存在三种情况,根据分类计数原理就需要将每种情况进行累加,就可以得到当前状态值的求解了。
其次就需要针对状态转移方程对dp表初始化了(防止越界,比如如果i<3 ,那么i-3<0发生报错)。
对1、2、3的dp值进行赋值即可。为什么不是0、1、2?因为0表示0级台阶,不存在意义,所以我们从1阶开始计算(后续创建dp表注意到开辟空间为n+1)。
1阶对应1种上楼梯方式,2阶对应两种(1步1步上,直接上两步),3阶对应4种(0阶(地面)直接三步上来,1阶两步上来,2阶1步上来)。
填表顺序自然是从左到右,因为我们需要先知道i-1、i-2、i-3的值。
题目要求我们返回对于n阶楼梯,小孩有多少种上楼梯的方式,那么返回值就是对应dp[n]即可。
编码:
编码一般遵循:1.创建dp表2.初始化3.填表的操作。根据上述思路一步一步来即可。
此题注意模的计算。
class Solution {
public:
int waysToStep(int n) {
if (n < 3) return n;
const int M = 1e9 + 7;
// 创建dp表
vector<int> dp(n + 1);
// 初始化
dp[1] = 1, dp[2] = 2, dp[3] = 4;
// 填表
for (int i = 4; i <= n; ++i)
dp[i] = ((dp[i - 1] + dp[i - 2]) % M + dp[i - 3]) % M;
return dp[n];
}
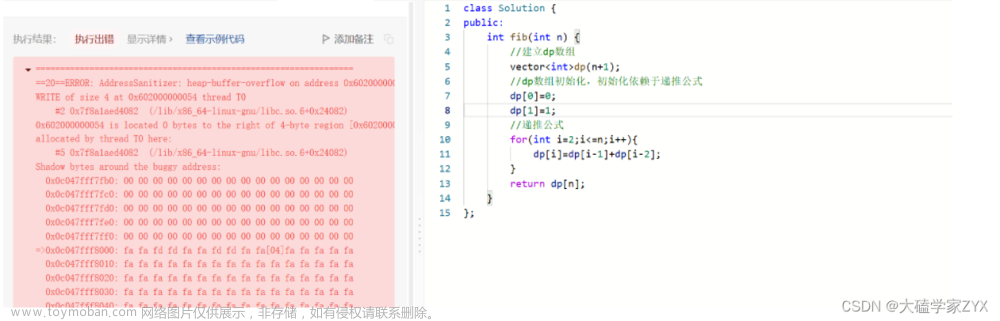
};注意上面只是介绍了基本的dp解题过程,其中对于dp表是存在优化的,可以将空间复杂度On降级为O1。
四、例题3-使用最小花费爬楼梯
题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
解析题目:
此题简单描述一下定义不同状态解题的区别。
1.定义状态表示:以i结尾
即dp[i] = 到下标为i的台阶的最低费用。
分析当前状态值如何求解,题目告诉我们在当前i阶花费cost[i]可以向上爬1层或者两层,那么当前i层是之前i-1阶花费钱爬一层或者之前i-2阶花费钱爬两层得到的,即:
状态转移方程:
dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])
初始化0、1即可。根据题目,可以选择从下标为0和1的台阶开始向上爬,那么dp[0] 和dp[1]都应该为0。
填表顺序从左到右(先需要知道左边的dp状态值)。
题目让我们返回到达楼梯顶部的最低花费,即dp[n];
2.定义状态表示:以i开始
即dp[i] = 从下标为i的台阶开始到楼梯顶部的最低费用。
注意到此时的状态表示发生了变化,那么就近进行分析,因为当前花费cost[i] 我们可以选择爬1层和爬2层,如果爬1层后是最低费用就爬此,否则就爬另外的一个,如此,就有如下的结果:
状态转移方程:
dp[i] = min(dp[i + 1], dp[i + 2]) + cost[i];
此时由于状态表示发生了变化,根据递推方程,初始化的方式也发生了变化,我们需要从后往前进行赋值,可以发现实际上我们可以直接求得dp[n - 1]和dp[n - 2]的值(此时dp[n]=0不存在意义了,到达顶层可以是最后一级台阶花费爬一步,或者倒数第二级台阶花费爬两步),所以初始化dp[n - 1]、dp[n - 2]即可。dp[n - 1] = cost[n - 2], dp[n - 2] = cost[n - 1]。
填表顺序为从右到左,我们需要先知道较大下标的值才能求解较小下标的状态值。
题目让我们返回到达楼梯顶部的最低花费,因为我们可以选择0、或者1开始往上爬,根据dp值只需要两者之间比较较小的花费返回即可:min(dp[0], dp[1]);
可以看到,我们将状态定义的不同,后续步骤方程基本不一样,所以定义状态按照自己习惯或者合适的场景进行理解。
编码:
1.以i结尾
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
// 解法1 设置dp表中的状态表示为到第i台阶花费的最低花费
int n = cost.size();
// 创建dp表
vector<int> dp(n + 1);
//初始化
dp[0] = dp[1] = 0;
// 填表
for (int i = 2; i <= n; ++i)
dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
return dp[n];
}
};2.以i开始
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
// 解法2 设置dp表中的状态表示为从第i台阶开始到顶部的最低花费总和
int n = cost.size();
// 创建dp表
vector<int> dp(n);
// 初始化
dp[n - 1] = cost[n - 1], dp[n - 2] = cost[n - 2];
// 填表
for (int i = n - 3; i >= 0; --i)
dp[i] = min(dp[i + 1], dp[i + 2]) + cost[i];
return min(dp[0], dp[1]);
}
};五、例题4-解码方法
题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台

解析题目:
针对此题,我们可以提出另外的一种优化方式,来优化我们的动态规划编码,使其看的非常整洁。
状态的定义我们就以习惯的以i结尾...:s中以i下标结尾时解码方法的总数。
dp[i] = s中以i下标结尾时解码方法的总数。
对于当前状态值得求解,分析题目,数字可以单独被解码,也可以两个结合解码。
对于一个在s中对应i下标得数字,存在单独解码和结合解码两种思路讨论,那么是和前面结合还是后面结合呢?注意看我们的状态定义:是以i下标结尾时的解码方法总数,不包括后面的解码的,所以是和前面的一个数进行结合解码。

在细分的去划分,存在解码成功和解码失败。单个解码只要大于0解码成功,否则解码失败,结合解码需要大于等于10、小于26解码成功,否则失败(题目要求:06、60类似这种解码失败) 。
如果单独解码成功,那么实际上就是在以i-1解码方法的基础上,后面添加了个字母,失败的话,那么以i结尾的解码方法总数加上0。
例子:i=2
s="112"
i - 1 = 1的解码方法总数:2
1、1 aa
11 k
那么2单解码成功
i此时的解码方法总数为:0+2
1、1、2 aab
11、2 kb
如果结合解码成功,那么实际上就是在i-2解码方法的基础上,后面添加了个字母,失败的话,那么以i结尾的解码方法总数加上0.
例子:i=2
s="112"
i - 2 = 0的解码方法总数:1
1 a
那么2结合解码成功
i此时的解码方法总数为:0+1
1、12 aL

综上,我们可以得到状态转移方程为:
状态转移方程:
dp[i] = (if int(s[i]) > 0: dp[i - 1] else: 0) +
(if 10 <= int(s[i-1] + s[i]) <= 26: dp[i - 2] else :0)
得到状态转移方程后我们需要进行初始化。
需要注意此处的初始化,正常情况下我们需要初始化0、1从而满足dp表不越界的情况,对应的求解dp[1]下标结尾的解码方法总数和状态转移方程有些一样,如果像原本那样写在外面会造成代码存在一定的冗余,我们可以将原本的dp数组扩大一个单位,整体右移。这样多出的一个就可以用来初始化s[1]了。

此时新增的第一位称作虚拟位,一般虚拟位的值为0(一般情况下,要结合实际情况,此题情况就不为0).这样就可以将旧dp[1]繁琐的步骤进行优化。
根据图示,需要注意的是:
1.虚拟节点内的值,需要保证后续的填表是正确的。(一般情况下是0正确的,但是在此题是错误的,要填1 -分析)
2.注意下标的映射关系 dp和s对应的关系。
此题需要满足优化后dp[2] 为s下下标为1的解码总数,根据递推公式,如果结合解码成功,需要加上i - 2的dp值,也就是此时对应虚拟节点的对应值,不能给0的原因在这里,给0的话,那么此时结合解码就失效了,所以需要加1,此时虚拟节点的值给予1即可。
填表顺序就是从左到右了,返回值根据是否优化返回dp[n]或者dp[n-1]表示此串s编码的解码方法总数了。
编码:
1.初始化不优化
class Solution {
public:
int numDecodings(string s) {
int n = s.size();
// 建立dp表 状态标识:到第i个编码的解码方法总数
vector<int> dp(n);
// 初始化
dp[0] = s[0] != '0';
if (n == 1) return dp[0];
if ((s[1] - '0') > 0) dp[1] += dp[0];
int tmp = (s[0] - '0') * 10 + (s[1] - '0');
if (tmp >= 10 && tmp <= 26) dp[1] += 1;
// 填表 递推公式:第i个可以单独编码 dp[i] += dp[i - 1] 第i个和第i-1个可以凑在一起编码 dp[i] += dp[i - 2]
for (int i = 2; i < n; ++i)
{
if (s[i] - '0' > 0) dp[i] += dp[i - 1];
tmp = (s[i - 1] - '0') * 10 + s[i] - '0';
if (tmp >= 10 && tmp <= 26) dp[i] += dp[i - 2];
}
return dp[n - 1];
};可以看到初始化有点繁琐不简洁,而下面优化后的方案就非常简洁了。 文章来源:https://www.toymoban.com/news/detail-765850.html
2.初始化优化文章来源地址https://www.toymoban.com/news/detail-765850.html
class Solution {
public:
int numDecodings(string s) {
int n = s.size();
// 建立dp表 状态标识:到第i个编码的解码方法总数
vector<int> dp(n + 1);
// 初始化 优化初始化
dp[0] = 1;
dp[1] = s[0] != '0';
if (n == 1) return dp[1];
// 填表 递推公式:第i个可以单独编码 dp[i] += dp[i - 1] 第i个和第i-1个可以凑在一起编码 dp[i] += dp[i - 2]
for (int i = 2; i <= n; ++i)
{
if (s[i - 1] - '0' > 0) dp[i] += dp[i - 1];
int tmp = (s[i - 2] - '0') * 10 + s[i - 1] - '0';
if (tmp >= 10 && tmp <= 26) dp[i] += dp[i - 2];
}
return dp[n];
}
};到了这里,关于【算法学习】斐波那契数列模型-动态规划的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!