【FOA三维路径规划】果蝇算法无人机避障三维航迹规划【含Matlab源码 3680期】-Toy模板网

这篇具有很好参考价值的文章主要介绍了【FOA三维路径规划】果蝇算法无人机避障三维航迹规划【含Matlab源码 3680期】。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

【FOA三维路径规划】果蝇算法无人机避障三维航迹规划【含Matlab源码 3680期】,Matlab路径规划（高阶版）,matlab

⛄一、果蝇算法无人机避障三维航迹规划简介

1 无人机航迹规划问题的数学模型
建立三维航迹规划问题的数学模型时, 不但考虑无人机基本约束, 还考虑复杂的飞行环境, 包括山体地形和雷暴威胁区。

1.1 无人机基本约束
规划的无人机三维航迹, 通常需要满足一些基本约束, 包括最大转弯角、最大爬升角或下滑角、最小航迹段长度、最低和最高飞行高度, 以及最大航迹长度等约束。其中, 最大转弯角约束, 是指无人机只能在水平面内小于或等于指定的最大转弯角内转弯;最大爬升角或下滑角约束, 是指无人机只能在垂直平面内小于或等于指定的最大爬升角或下滑角内爬升或下滑;最小航迹段长度约束, 要求无人机改变飞行姿态之前, 按目前的航迹方向飞行的最短航程;最低和最高飞行高度约束, 要求无人机在指定的飞行高度区间飞行;最大航迹长度约束, 是指无人机的航迹长度小于或等于指定的阈值。

记q (x, y, z, θ, ψ) 为无人机的飞行位置与姿态, 其中, (x, y, z) 为无人机的位置, θ为无人机的水平转弯角, ψ为无人机的竖直爬升角或下滑角, 进而建立上述基本约束的数学表达式。
【FOA三维路径规划】果蝇算法无人机避障三维航迹规划【含Matlab源码 3680期】,Matlab路径规划（高阶版）,matlab
1.2 飞行环境障碍物和威胁区建模
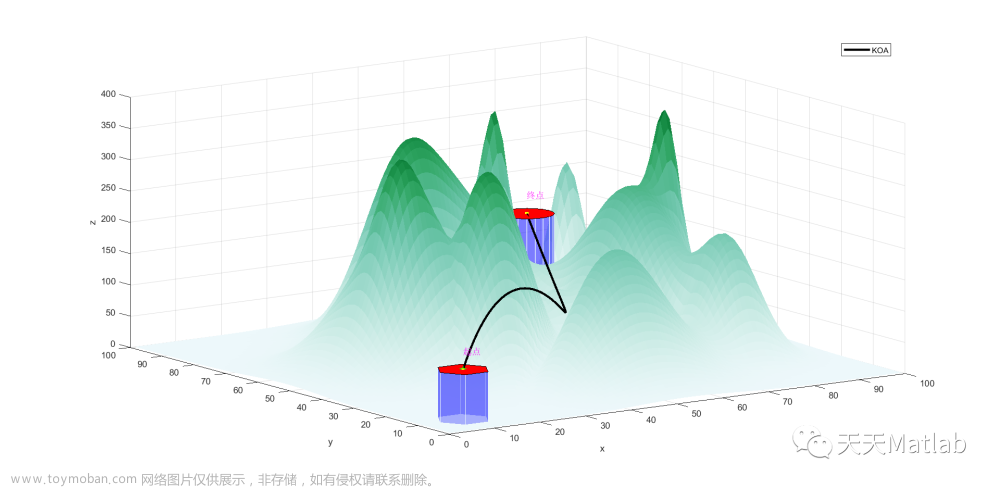
在飞行环境中, 高耸的山体近似采用圆锥体等效表示, 用以e为底的自然指数图形生成, 那么, 山体地形可以通过多个位置不同的圆锥体叠加而成。若将参考海拔基准高度设置为xOy平面, 记 (x, y, z) 为山体地形中的点, 那么
【FOA三维路径规划】果蝇算法无人机避障三维航迹规划【含Matlab源码 3680期】,Matlab路径规划（高阶版）,matlab
式中:N为山体个数;xk0和yk0为第k座山体中心对称轴的横坐标和纵坐标;hk为第k座山体的最大高度;xki和yki为第k座山体的横向斜度和纵向斜度。

在飞行环境中, 山体附近通常存在雷暴等极端气象, 本文视为飞行威胁区, 并通过球体近似等效表示, 且记第k座山体附近飞行威胁区的球心坐标为 (xks0, yks0, zks0) , 半径为rk。

1.3 目标函数及航迹表示
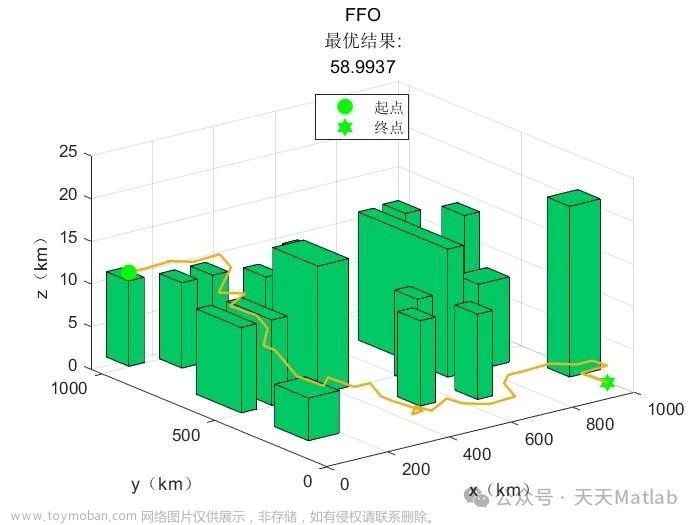
在本文中, 执行任务的某型无人机, 其航迹规划的目标函数是生成一条由起始点到目标点的无碰撞可行航迹。采用q (x, y, z, θ, ψ) 表示无人机在飞行空域中某特定位置的特定姿态, 那么 (x, y, z) 则表示无人机所在航迹点, θ表示无人机的水平转弯角, ψ表示无人机的竖直爬升角或下滑角。采用r (q) 表示由起始点qinitial到目标点qgoal的无碰撞可行航迹, 那么航迹规划的过程可以写成如下形式:
【FOA三维路径规划】果蝇算法无人机避障三维航迹规划【含Matlab源码 3680期】,Matlab路径规划（高阶版）,matlab

2 果蝇算法
果蝇优化算法（FOA）是一种基于果蝇觅食行为推演出寻求全局优化的新方法。果蝇本身在感官知觉上优于其他物种，尤其是嗅觉和视觉上。果蝇的嗅觉器官能很好的搜集漂浮在空气中的各种气味，甚至能够嗅到40公里以外的食物源。然后，飞到食物位置附近后亦可使用敏锐的视觉发现食物和同伴聚集的位置，并且向该方向飞去。

果蝇群体迭代搜寻食物的步骤如下：

（1）随机初始化果蝇群体位置。

      Init X_axis

      Init Y_axis

（2）赋予果蝇个体利用嗅觉搜寻食物的随机距离与方向。

      Xi = X_axis + Random Value

      Yi = Y_axis + Random Value

（3）由于无法得知食物的位置，因此先估计与原点的距离（Dist），再计算味道浓度判定值（S），此值为距离的倒数。

      Disti = sqrt(Xi^2 + Yi^2)

      Si = 1 / Disti

（4）味道浓度判定值（S）代入味道浓度判定函数（或称为Fitness function）以求出该果蝇个体位置的味道浓度（Smelli）。

      Smelli = Function(Si)

（5）找出该果蝇群体中味道浓度最高的果蝇（求极大值）。

      [bestSmell bestIndex] = max(Smell)

（6）保留最佳味道浓度值与x、y的坐标，此时果蝇群体利用视觉往该位置飞去。

      Smellbest = bestSmell

      X_axis = X(bestIndex)

      Y_axis = Y(bestIndex)

（7）进入迭代寻优，重复执行步骤2-5，并判断味道浓度是否优于前一迭代味道浓度，若是则实行步骤6。

⛄二、部分源代码

%% 三维地图-无人机寻路
% 3D map - aircraft pathfinding
%% 这是使用原始算法的直接求解结果，添加专用于本问题的更新方式可以进一步提高精度
% This is the direct result of using the original algorithm,
% adding some specific update methods to this problem can further improve the accuracy
clc;
clear;
close all;
warning off

%% 载入数据
data.S=[1,950,12]; %起点位置
data.E=[950,1,1]; %终点点位置
data.Obstacle=xlsread(‘data.xls’);
data.numObstacles=length(data.Obstacle(:,1));
data.mapSize=[1000,1000,20]; %10m 地图尺寸
data.unit=[50,50,1]; %地图精度
data.S0=ceil(data.S./data.unit);
data.E0=ceil(data.E./data.unit);
data.mapSize0=data.mapSize./data.unit;
data.map=zeros(data.mapSize0);
figure
plot3(data.S(:,1),data.S(:,2),data.S(:,3),‘o’,‘LineWidth’,1,…
‘MarkerEdgeColor’,‘g’,…
‘MarkerFaceColor’,‘g’,…
‘MarkerSize’,8)
hold on
plot3(data.E(:,1),data.E(:,2),data.E(:,3),‘h’,‘LineWidth’,1,…
‘MarkerEdgeColor’,‘g’,…
‘MarkerFaceColor’,‘g’,…
‘MarkerSize’,8)
for i=1:data.numObstacles
x=1+data.Obstacle(i,1);
y=1+data.Obstacle(i,2);
z=1+data.Obstacle(i,3);
long=data.Obstacle(i,4);
wide=data.Obstacle(i,5);
pretty=data.Obstacle(i,6);
[V,F] = DrawCuboid(long, wide, pretty, x,y,z);
x0=ceil(x/data.unit(1));
y0=ceil(y/data.unit(2));
z0=ceil(z/data.unit(3));
long0=ceil(long/data.unit(1));
wide0=ceil(wide/data.unit(2));
pretty0=ceil(pretty/data.unit(3));
data.map(x0:x0+long0,y0:y0+wide0,z0:z0+pretty0)=1;
end
legend(‘起点’,‘终点’)
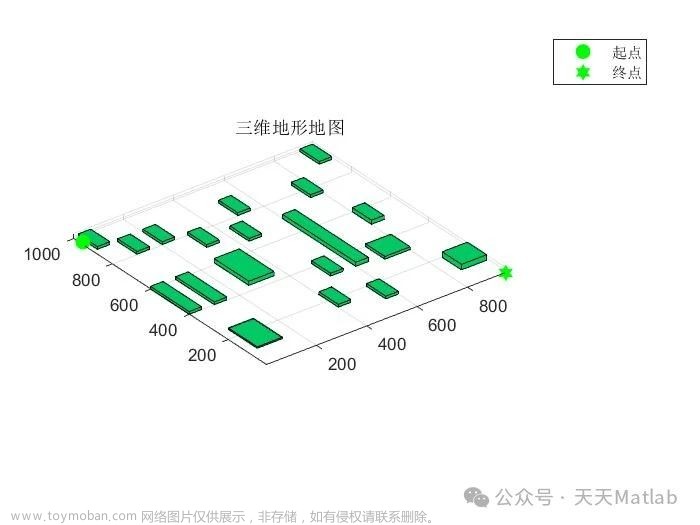
title(‘三维地形地图’)
grid on
axis equal
%%
% index=find(data.map==1);
% [p1,p2,p3] = ind2sub(size(data.map), index);
% figure
% plot3(data.S0(:,1),data.S0(:,2),data.S0(:,3),‘o’,‘LineWidth’,1,…
% ‘MarkerEdgeColor’,‘g’,…
% ‘MarkerFaceColor’,‘g’,…
% ‘MarkerSize’,8)
% hold on
% plot3(data.E0(:,1),data.E0(:,2),data.E0(:,3),‘h’,‘LineWidth’,1,…
% ‘MarkerEdgeColor’,‘g’,…
% ‘MarkerFaceColor’,‘g’,…
% ‘MarkerSize’,8)
% plot3(p1,p2,p3,‘.’,‘LineWidth’,1,…
% ‘MarkerEdgeColor’,‘k’,…
% ‘MarkerFaceColor’,‘g’,…
% ‘MarkerSize’,10)
% legend(‘起点’,‘终点’)
% title(‘三维地形地图’)
% grid on
% axis equal
% xlabel(‘x（km）’)
% ylabel(‘y（km）’)
% zlabel(‘z（km）’)
%% 生成可移动方向
temp=[1,0,-1];
direction=[];
for i=1:3
for j=1:3
for k=1:3
direction=[direction;temp(i),temp(j),temp(k)];
end
end
end
position=find(direction(:,1)==0 & direction(:,2)==0 & direction(:,3)==0);
direction(position,:)=[];
data.direction=direction;

%% 算法参数设置 Parameters
% 基本参数
numAgent=20; %种群个体数 size of population，可自行修改
Max_iter=20; %最大迭代次数 maximum number of interation，可自行修改
lb=0;%下限，可自行修改
ub=1;%上限，可自行修改
dim=prod(data.mapSize0); % 优化变量个数
fobj=@(x) aimFcn(x,data);%目标函数，用以优化

%% 使用优化算法求解

Optimal_results{2,index}=recording;%迭代曲线
Optimal_results{3,index}=bestY;%最佳函数值
Optimal_results{4,index}=bestX; %最佳变量值
Optimal_results{5,index}=result; %优化结果
Optimal_results{6,index}=toc; %运行时间
index = index +1;