图论与算法（2）图的基本表示-Toy模板网

这篇具有很好参考价值的文章主要介绍了图论与算法（2）图的基本表示。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1. 图的分类

（1）有向图和无向图：

有向图（Directed Graph）：图中的边具有方向，表示节点之间的单向关系。
无向图（Undirected Graph）：图中的边没有方向，表示节点之间的双向关系。

（2）加权图和无权图：

加权图（Weighted Graph）：图中的边具有权重或距离，表示节点之间的关系有一定的度量值。
无权图（Unweighted Graph）：图中的边没有权重，表示节点之间的关系仅表示存在与否。

（3）简单图和多重图：

简单图（Simple Graph）：图中不存在自环边（从节点到自身的边）和重复边（连接相同节点对的多条边）。
多重图（Multigraph）：图中允许存在自环边和重复边。

（4）连通图和非连通图：

连通图（Connected Graph）：图中任意两个节点之间都存在路径，即图中没有孤立节点或子图。
非连通图（Disconnected Graph）：图中存在孤立节点或多个不相连的子图。

（5）有环图和无环图：

有环图（Cyclic Graph）：图中存在环，即从一个节点出发经过若干条边可以回到该节点。
无环图（Acyclic Graph）：图中不存在环。

（6）完全图和非完全图：

完全图（Complete Graph）：图中的任意两个节点之间都存在边，即每个节点都与其他所有节点直接相连。
非完全图（Non-complete Graph）：图中存在节点对之间不存在直接连接的边。

2. 图的顶点vertex与边Edge

在图论中，图由顶点（vertices）和边（edges）组成。顶点代表图中的个体或实体，而边表示顶点之间的关系或连接。这种连接可以是有向的或无向的，具体取决于图的类型和定义。

图论平行连接,设计模式与算法,算法,图论,图的表示,权,度

2.1 顶点（Vertices）：

图中的顶点（Vertex），也被称为节点（Node），是图论中的基本元素之一。顶点是图中的个体或实体，可以代表不同的对象、事件、位置等，具体取决于图的应用领域和问题。

在图中，顶点通常用标识符或编号来表示，以便进行标识和访问。每个顶点可以具有一些属性或值，以便更好地描述和表示图中的内容。这些属性可以是任意的，根据具体的问题和应用进行定义，例如顶点的名称、权重、坐标等。

2.2 边（Edges）

图中的顶点通过边（Edge）相互连接，边表示了顶点之间的关系或连接。边可以是有向的（带有方向的箭头），也可以是无向的（没有方向）。通过边的连接，顶点之间形成了图中的网络结构，可以通过顶点和边的组合来描述和分析各种复杂的关系和问题。

边是顶点之间的连接关系，表示图中的关联或交互。

边可以是有向的，也可以是无向的。

有向边（Directed Edge）具有方向，表示从一个顶点指向另一个顶点的关系。
无向边（Undirected Edge）没有方向，表示两个顶点之间的对等关系。

通过顶点和边的组合，可以构建出不同类型的图，如有向图、无向图、加权图等

3. 无向图与有向图

图论平行连接,设计模式与算法,算法,图论,图的表示,权,度

3.1 无向图

无向图（Undirected Graph）：无向图是一种图，其中顶点之间的边没有方向。换句话说，如果顶点 A 与顶点 B 之间存在边，那么从 A 到 B 和从 B 到 A 都是允许的。

无向图的边可以表示成无序的连接，意味着两个顶点之间的连接是相互的。

地铁站交汇点和社交网络中的好友关系都可以使用无向图来建模，因为它们都是相互的关系，没有明确的方向性。

3.2 有向图

有向图（Directed Graph）：有向图是一种图，其中顶点之间的边具有方向。换句话说，如果顶点 A 与顶点 B 之间存在一条有向边，那么从 A 到 B 的方向是明确的，并且不一定存在从 B 到 A 的有向边。

有向图中的边表示从一个顶点到另一个顶点的单向关系，其中一个顶点是起始点，另一个是终止点。

抖音的关注功能是一个典型的有向图场景，其中一个用户可以关注另一个用户，但并不意味着另一个用户也会关注回去。

无向图和有向图在图论中都是重要的概念，它们用于描述不同类型的关系和连接。

4. 图的权 Weight

在图论中，图的权（Weight）指的是在图的边上赋予的一个数值或度量，用于表示顶点之间的关系或连接的强度、距离、成本等信息。

（1）针对权可以将图分为有权图、无权图两种：

图论平行连接,设计模式与算法,算法,图论,图的表示,权,度

（2）如果根据边是否具有权重、是否有向，又可以将图分为四种类型：无向无权图、无向有权图、有向无权图、有向有权图。

4.1 无向无权图

无向无权图（Undirected Unweighted Graph）：无向无权图是一种图，其中顶点之间的边没有权重。边的存在只表示两个顶点之间的连接，没有其他额外的信息。

在无向无权图中，边可以看作是没有方向的，可以从一个顶点到另一个顶点，也可以反向。无向无权图常用于描述简单的关系，如社交网络中的好友关系，地图中的道路连接等。

4.2 无向有权图

无向有权图（Undirected Weighted Graph）：无向有权图是一种图，其中顶点之间的边具有权重。边的权重可以表示顶点之间的距离、成本、强度等。

在无向有权图中，边是无方向的，权重值可以在两个顶点之间是对称的，即从顶点 A 到顶点 B 的权重与从顶点 B 到顶点 A 的权重相同。无向有权图常用于表示带权重的关系网络，如城市之间的交通网络，通信网络等。

4.3 有向无权图

有向无权图（Directed Unweighted Graph）：有向无权图是一种图，其中顶点之间的边没有权重，并且具有方向。边的方向表示了从一个顶点到另一个顶点的单向关系。

在有向无权图中，边只表示从一个顶点到另一个顶点的连接，没有其他额外的信息。有向无权图常用于描述有向关系的场景，如网页之间的链接关系，传感器网络中的数据流向等。

4.4 有向有权图

有向有权图（Directed Weighted Graph）：有向有权图是一种图，其中顶点之间的边具有权重，并且具有方向。边的权重表示了从一个顶点到另一个顶点的单向关系的度量值。

在有向有权图中，边的权重和方向是有关联的，从一个顶点到另一个顶点的权重值可以与反向的权重值不同。有向有权图常用于表示有向关系和权重的复杂网络，如交通流量网络、物流网络等。

5. 图的边

图论平行连接,设计模式与算法,算法,图论,图的表示,权,度

5.1 自环边

自环边（Self-loop）：自环边是指连接图中的一个顶点与其自身的边。换句话说，自环边起点和终点是同一个顶点。自环边在无向图和有向图中都可以存在，但在无向图中自环边没有方向。

示例：

在无向图中，如果一个顶点连接到自己，就形成了一个自环边。例如，顶点 A 与自身相连的边 (A, A) 就是一个自环边。

在有向图中，从顶点 A 指向自身的边 (A, A) 也是一个自环边。

自环边的存在表示了顶点自身的某种特殊关系或属性。在某些应用中，自环边可能具有特殊的含义，例如表示顶点本身的特性或状态。

5.2 平行边

平行边（Parallel Edge）：平行边是指连接同一对顶点的多条边。换句话说，如果两个顶点之间存在多条边，这些边被称为平行边。平行边可以在无向图和有向图中存在。

示例：

在无向图中，如果顶点 A 和顶点 B 之间存在多条边，如边 (A, B) 和边 (B, A)，则这些边就是平行边。

在有向图中，如果从顶点 A 到顶点 B 存在多条有向边，如边 (A, B) 和边 (A, B')，则这些边也是平行边。

平行边的存在表示了顶点之间的多重关系或连接。它们可以表示不同的权重、不同的关系类型或不同的路径。在一些应用中，平行边可能具有不同的语义或含义。

6. 简单图与多重图

图论平行连接,设计模式与算法,算法,图论,图的表示,权,度

6.1 简单图

简单图（Simple Graph）：简单图是指没有自环边（连接一个顶点到自身）和平行边（连接相同一对顶点）的图。换句话说，简单图中每条边都是唯一的，且顶点之间的连接关系是简洁明确的。在简单图中，任意两个顶点之间最多只有一条边相连。例如，一个包含4个顶点和3条边的图就是一个简单图。

6.2 多重图

多重图（Multigraph）：多重图是指允许存在平行边的图，即可以有多条连接相同一对顶点的边。换句话说，多重图中同一对顶点之间可以有多条边。与简单图不同，多重图中的边可以重复出现。例如，一个包含4个顶点和4条边，其中两条边连接同一对顶点的图就是一个多重图。

简单图和多重图的区别在于边的重复性。在简单图中，每对顶点之间最多只能有一条边，而在多重图中，同一对顶点之间可以有多条边。

7. 联通分量与树

7.1 概念

在图论中，连通分量是指无向图或有向图中的一个最大连通子图。连通分量由一组顶点组成，其中任意两个顶点之间存在路径，而与其他顶点不相连。换句话说，连通分量是一组顶点的最大子集，其中任意两个顶点都可以通过路径相互到达。

在无向图中，连通分量是指由顶点和边构成的一个子图，其中任意两个顶点之间存在路径。如果无向图是连通的，那么它只有一个连通分量，即整个图本身。

在有向图中，连通分量是指由顶点和边构成的一个子图，其中任意两个顶点之间存在有向路径。有向图的连通分量可以是强连通分量（Strongly Connected Components）或弱连通分量（Weakly Connected Components）。强连通分量是指在有向图中，任意两个顶点之间存在双向路径，而弱连通分量是指在有向图中，将有向边的方向忽略后，任意两个顶点之间存在路径。

连通分量的概念帮助我们理解图的结构和连通性。通过识别和分析连通分量，我们可以研究图的属性、性质和算法，从而更好地理解和解决与图相关的问题。

7.2 一个图可能有多个联通分量

图论平行连接,设计模式与算法,算法,图论,图的表示,权,度

一个图的所有节点不一定全部相连，一个图可能有多个联通分量。

7.3 树与无环图、有环图

图论平行连接,设计模式与算法,算法,图论,图的表示,权,度

树是一种无环图：树是一种特殊的无环图，它由节点（顶点）和边组成，并且满足没有任何环（回路）的条件。

无环图不一定是树：无环图是指没有任何环（回路）的图，它可以是有向图或无向图。无环图可以包含多个独立的联通分量，每个联通分量都是一个无环图。因此，并非所有无环图都满足树的特点，因为它们可能缺少连接所有节点的必要条件。

联通的无环图是树：当一个无环图是联通的，并且满足每个节点都有且仅有一个父节点（除了根节点）的条件时，它被称为树。联通的无环图具备了树的特点，其中每个节点都可以通过边相互连接，并且不存在环。

7.4 连通图与树

问题：连通图的生成树包含所有的顶点的树，其边数是 V-1，反过来说：包含所有顶点，边数V-1，一定是连通图的生成树吗？

图论平行连接,设计模式与算法,算法,图论,图的表示,权,度

在连通图中，包含所有顶点并且边数为 V-1 的子图被称为生成树。然而，反过来并不一定成立，即包含所有顶点并且边数为 V-1 的子图不一定是连通图的生成树。

如果有一个图具有 7 个顶点，边集为 {(1, 0), (1, 2), (1, 6), (0, 3), (2, 3), (3, 4)}，而顶点 5 没有与任何顶点相邻，那么包含所有顶点并且边数为 V-1 的子图不是连通图的生成树，因为它无法连接顶点 5。

7.5 一个图一定有生成树吗

图论平行连接,设计模式与算法,算法,图论,图的表示,权,度

非连通图不一定有生成树。生成树是一个连通图的最小连通子图，它保留了图中的所有顶点，并且通过删除一些边来确保没有环的存在。对于连通图而言，至少存在一棵生成树。

然而，如果一个图是非连通图，即由多个不相连的连通分量组成，那么每个连通分量都可以有自己的生成树。但整个图没有单一的生成树，因为无法通过边将所有顶点连接起来。

总结起来，连通图一定有生成树，而非连通图可能由多个连通分量的生成树组成，但整个图没有单一的生成树。

7.6一个图是否一定有生成森林

一个图一定有生成森林。

生成森林是指一个图中所有连通分量的生成树的集合。如果一个图是连通图，那么它的生成森林就只包含一个生成树。但如果一个图是非连通图，由多个不相连的连通分量组成，那么每个连通分量都可以有自己的生成树，从而形成整个图的生成森林。

生成森林保留了图中的所有顶点，并且通过删除一些边来确保没有环的存在。每个生成树都是生成森林中的一棵树，且它们互相独立，不共享顶点和边。

因此，无论图是连通图还是非连通图，都可以构成生成森林，其中连通图对应于单一的生成树，而非连通图对应于多个生成树组成的森林。

8.度 degree

对于无向图而言，一个顶点的度（degree）就是与该顶点相邻的边的数量。

图论平行连接,设计模式与算法,算法,图论,图的表示,权,度

在无向图中，顶点的度表示与该顶点直接相连的边的数量。每条边都连接两个顶点，因此对于一个顶点而言，与其相邻的边的数量就是它的度。

例如，如果在无向图中，一个顶点与其他三个顶点相邻，则该顶点的度为 3，表示它与三条边直接连接。

需要注意的是，对于有向图而言，顶点的度被分为入度（indegree）和出度（outdegree），分别表示指向该顶点和由该顶点出发的边的数量。

9. 邻接矩阵

9.1 概述

图的基本表示方法之一是邻接矩阵（Adjacency Matrix）。

邻接矩阵是一个二维矩阵，用来表示图中顶点之间的连接关系。对于一个有 V 个顶点的图，邻接矩阵是一个 V × V 的矩阵。矩阵的行和列分别对应图中的顶点，矩阵中的元素表示对应顶点之间是否存在边。

邻接矩阵的表示方法有两种常见的形式：布尔型和权重型。

9.1.1 布尔型邻接矩阵

布尔型邻接矩阵：在布尔型邻接矩阵中，矩阵的元素值为布尔值（通常是 0 和 1），表示对应顶点之间是否存在边。如果顶点 i 和顶点 j 之间存在边，则矩阵中的第 i 行第 j 列和第 j 行第 i 列的元素都为 1，否则为 0。

   | 1 | 2 | 3 |
--------------
 1 | 0 | 1 | 1 |
--------------
 2 | 1 | 0 | 0 |
--------------
 3 | 1 | 0 | 0 |

9.1.2 布尔型邻接矩阵

权重型邻接矩阵：在权重型邻接矩阵中，矩阵的元素值表示对应边的权重或距离。如果顶点 i 和顶点 j 之间存在边，则矩阵中的第 i 行第 j 列和第 j 行第 i 列的元素表示该边的权重或距离。如果两个顶点之间没有边，则元素值通常为无穷大或一个特定的标记值。

   | 1 | 2 | 3 |
--------------
 1 | 0 | 2 | 3 |
--------------
 2 | 2 | 0 | ∞ |
--------------
 3 | 3 | ∞ | 0 |

邻接矩阵的优点是可以快速判断任意两个顶点之间是否存在边，查找某个顶点的相邻顶点也很高效。然而，它的缺点是占用较大的空间，尤其在稀疏图（边数远小于顶点数的图）的情况下，大部分的矩阵元素都是 0，造成空间浪费。

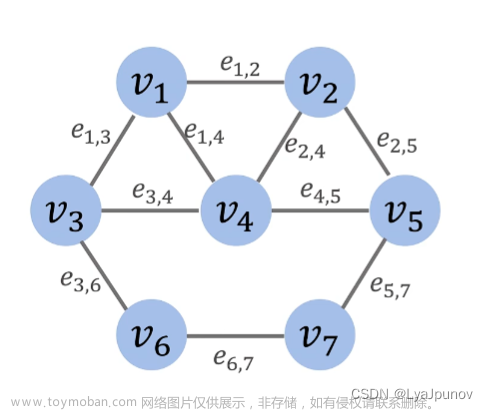
9.2 示例-无权无向图

9.2.1 图与矩阵的对应

图论平行连接,设计模式与算法,算法,图论,图的表示,权,度

上图是无权无向图，对应下列的邻接矩阵。比如：A[i][j]=1 表示顶点 i 和顶点 j 相邻对于简单图：主对角线为0.

   | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
-------------------------------
 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
-------------------------------
 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 |
-------------------------------
 2 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
-------------------------------
 3 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
-------------------------------
 4 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
-------------------------------
 5 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
-------------------------------
 6 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |

9.2.2 图-数-邻接矩阵

图论平行连接,设计模式与算法,算法,图论,图的表示,权,度

9.2.3 邻接矩阵表示图

/**
 * 1.当前图的空间复杂度：O(V^2)
 * 2.时间复杂度：
 *     建图： O(E)
 *     查看两点是否相邻：O(1)
 *     求一个点的相邻节点：O（V）
 * @author wushaopei
 * @create 2023-06-02 15:05
 */
public class AdjMatrix {

    private int V;           // 顶点数
    private int E;           // 边数
    private int[][] adj;     // 邻接矩阵

    /**
     * 构造函数，根据指定的文件名创建邻接矩阵表示的图。
     * @param fileName 包含图信息的文件名
     */
    public AdjMatrix(String fileName) {
        // 从文件中读取图的信息
        File file = new File(fileName);
        try (Scanner scanner = new Scanner(file)){
            V = scanner.nextInt();
            if ( V < 0 ) throw new IllegalArgumentException("V must be non-negative");
            E = scanner.nextInt();
            if ( E < 0 ) throw new IllegalArgumentException("V must be non-negative");

            adj = new int[V][V];
            for (int i = 0; i < E; i ++){
                int a = scanner.nextInt();
                validateVertex(a);
                int b = scanner.nextInt();
                validateVertex(b);

                if (a == b) throw new IllegalArgumentException("Self Loop is Detected!");
                // 检测平行边
                if (adj[a][b] == 1) throw new IllegalArgumentException("Parallel Edges are Detected!");

                adj[a][b] = 1;
                adj[b][a] = 1;
            }
        } catch (FileNotFoundException e) {
            e.printStackTrace();
        }
    }

    /**
     * 验证顶点的有效性。
     * @param v 待验证的顶点
     */
    private void validateVertex(int v){
        if ( v < 0 && v > V){
            throw new IllegalArgumentException("vertex " + v + " is invalid.");
        }
    }

    /**
     * 计算顶点的度（即相邻节点的数量）。
     *
     * @param v 待计算度的顶点
     * @return 顶点v的度
     */
    public int degree(int v){
        return adj(v).size();
    }

    /**
     * 返回邻接矩阵的字符串表示
     * @return
     */
    @Override
    public String toString() {
        StringBuffer stringBuffer = new StringBuffer();
        stringBuffer.append(String.format("   "));
        for (int i = 0 ; i < V; i ++){
            stringBuffer.append(String.format(" %s ", i));
        }

        for (int i = 0 ; i < V; i ++){
            stringBuffer.append("\n");
            stringBuffer.append(String.format(" %s ",i));
            for (int j = 0; j < V; j ++){
                stringBuffer.append(String.format(" %s ", adj[i][j]));
            }
        }
        return stringBuffer.toString();
    }

    /**
     * 返回图的顶点数。
     * @return 图的顶点数
     */
    private int V(){
        return V;
    }

    /**
     * 返回图的边数。
     * @return 图的边数
     */
    private int E(){
        return E;
    }

    /**
     * 判断顶点v和w之间是否存在边。
     *
     * @param v 第一个顶点
     * @param w 第二个顶点
     * @return 如果顶点v和w之间存在边，则返回true；否则返回false
     */
    public boolean hashEdge(int v, int w){
        validateVertex(v);
        validateVertex(w);
        return adj[v][w] == 1;
    }

    /**
     * 返回顶点v的相邻节点列表。
     *
     * @param v 待查询相邻节点的顶点
     * @return 顶点v的相邻节点列表
     */
    public List<Integer> adj(int v){
        validateVertex(v);
        List<Integer> list = new ArrayList<>();
        for (int i = 0; i < V; i ++){
            if (adj[v][i] == 1){
                list.add(i);
            }
        }
        return list;
    }

    /**
     * 测试主函数。
     *
     * @param args 命令行参数
     */
    public static void main(String[] args) {

        AdjMatrix adjMatrix = new AdjMatrix("g.txt");
        System.out.println(adjMatrix.toString());
        System.out.println(adjMatrix.adj(1));
    }
}

下面是对各个操作的时间复杂度分析：

建图（构造函数）：O(E)，遍历输入的边数，将相应的邻接矩阵位置设置为1。
查看两点是否相邻（hasEdge方法）：O(1)，直接通过邻接矩阵中的值判断两个顶点之间是否存在边。
求一个点的相邻节点（adj方法）：O(V)，遍历指定顶点的邻接矩阵行，找到值为1的位置，将其加入到相邻节点列表中。

而空间复杂度为O(V^2)，因为邻接矩阵的大小与图的顶点数V有关，为V乘以V。

9.2.4 邻接矩阵的问题

假设一个图有3000个节点，我们来分析其空间复杂度、时间复杂度以及边的数量和相邻顶点的情况。

空间复杂度：对于邻接矩阵表示法，空间复杂度为O(V^2)，其中V为顶点数。在这种情况下，图有3000个节点，邻接矩阵的大小为3000 * 3000，因此空间复杂度为3000^2 = 9,000,000。

边数最小是： 3000 * 3/2 = 4500 条边；最多是： 3000 * 2999/2 = 4498500条边。

当前示例存在以下问题：

空间复杂度高：无论边数是最小值还是最大值，使用邻接矩阵来表示图都需要的空间复杂度是O(V^2)，即3000^2 = 9,000,000。这样的高空间复杂度会占用大量的内存资源。
空间浪费：如果实际图的边数接近最小值4500，那么使用邻接矩阵会浪费大量的空间，因为矩阵中的大部分元素都是0。这种浪费对于稀疏图尤为明显。
构建时间开销大：当边数增加到最大值4498500时，构建邻接矩阵需要遍历所有的边，并将对应的矩阵位置设置为1。这将耗费较多的时间和计算资源，尤其是在边数非常大时。

10. 稀疏图与稠密图

10.1 概述

稀疏图和稠密图是用来描述图中边的数量相对于顶点数量的概念。

图论平行连接,设计模式与算法,算法,图论,图的表示,权,度

（1）稀疏图

稀疏图：指的是边的数量相对较少的图。换句话说，稀疏图的顶点之间的连接相对较少。在稀疏图中，顶点之间可能存在较远的距离，或者存在许多孤立的顶点。邻接矩阵表示稀疏图时，大部分的元素都是0，而邻接表表示稀疏图时，每个顶点的邻接链表相对较短。

（2）稠密图

稠密图：指的是边的数量相对较多的图。换句话说，稠密图的顶点之间的连接相对较多。在稠密图中，顶点之间通常存在较短的距离，或者几乎所有的顶点都是相互连接的。邻接矩阵表示稠密图时，大部分的元素都是非零的，而邻接表表示稠密图时，每个顶点的邻接链表相对较长。

10.2 稀疏图和稠密图在边数上的影响

稀疏图和稠密图在边数上的影响主要体现在存储空间和算法复杂度上。

10.2.1 对于稀疏图：

边数相对较少，存储空间占用较小。使用邻接表来表示稀疏图可以更节省空间，因为邻接表只需要存储存在边的信息，而不需要为不存在的边分配空间。

在遍历和搜索算法中，由于边数较少，算法的时间复杂度相对较低。例如，对稀疏图进行深度优先搜索（DFS）或广度优先搜索（BFS）的时间复杂度通常为 O(V + E)，其中 V 是顶点数，E 是边数。

10.2.2 对于稠密图：

边数相对较多，存储空间占用较大。使用邻接矩阵来表示稠密图可以更有效地存储边的信息，因为邻接矩阵以矩阵的形式表示了所有顶点之间的连接关系，每个位置都需要存储边的状态信息。

在遍历和搜索算法中，由于边数较多，算法的时间复杂度相对较高。例如，对稠密图进行深度优先搜索（DFS）或广度优先搜索（BFS）的时间复杂度为 O(V^2)，其中 V 是顶点数，因为需要遍历邻接矩阵中的每个位置。

因此，当处理稀疏图时，使用邻接表可以更节省空间和降低算法复杂度；而在处理稠密图时，使用邻接矩阵可以更高效地存储和处理图的结构。根据具体应用场景和图的特征，选择适合的数据结构和算法可以提高效率和性能。

10.3 示例

当涉及到城市之间的路线网络时，稀疏图和稠密图的概念可以更清晰地理解。

假设有一个城市之间的路线网络，其中城市是图中的顶点，而路线是图中的边。我们来比较两种情况：

（1）稀疏图

稀疏图：如果这个路线网络是一个稀疏图，那么城市之间的直接连接较少。例如，有100个城市，但是只有100条直接的路线连接它们。在这种情况下，我们可以使用邻接表来表示图。邻接表仅存储存在的边，每个城市只需存储与其直接连接的路线信息，节省了存储空间。此外，在进行深度优先搜索（DFS）或广度优先搜索（BFS）等算法时，由于边数较少，算法的时间复杂度较低。

（2）稠密图

稠密图：如果这个路线网络是一个稠密图，那么城市之间的直接连接较多。例如，有100个城市，且每个城市都与其他99个城市直接相连，形成了完全图。在这种情况下，我们可以使用邻接矩阵来表示图。邻接矩阵以矩阵的形式表示了所有城市之间的连接关系，每个位置都需要存储边的状态信息。由于边数较多，使用邻接矩阵可以更有效地存储和处理图的结构。但是，在进行深度优先搜索（DFS）或广度优先搜索（BFS）等算法时，由于需要遍历邻接矩阵中的每个位置，算法的时间复杂度较高。

11.邻接表

11.1 概述

邻接表是一种常见的图的表示方法，它使用链表来表示图中每个顶点的相邻顶点。每个顶点对应一个链表，链表中存储了与该顶点直接相邻的顶点。

邻接表的优点是适用于表示稀疏图，可以有效地节省内存空间。对于稀疏图来说，顶点之间的边相对较少，使用邻接表可以只存储实际存在的边，减少了不必要的空间占用。

11.2 邻接表表示图

/**
 * 邻接表表示图的类
 * @author wushaopei
 * @create 2023-06-02 15:05
 */
public class AdjList {

    private int V;           // 顶点数
    private int E;           // 边数
    private LinkedList<Integer>[] adj;     // 邻接表

    /**
     * 构造函数，通过读取文件构建邻接表
     * @param fileName 文件名
     */
    public AdjList(String fileName) {
        // 从文件中读取图的信息
        File file = new File(fileName);
        try (Scanner scanner = new Scanner(file)){
            V = scanner.nextInt();  // 读取顶点数
            if (V < 0 ) throw new IllegalArgumentException("V must be non-negative");
            adj = new LinkedList[V];  // 创建邻接表数组
            for (int i = 0; i < V; i ++){
                adj[i] = new LinkedList<>();  // 初始化邻接表中的每个链表
            }

            E = scanner.nextInt();  // 读取边数
            if (E < 0 ) throw new IllegalArgumentException("V must be non-negative");
            for (int i = 0; i < E; i ++){
                int a = scanner.nextInt();  // 读取边的一个顶点
                validateVertex(a);
                int b = scanner.nextInt();  // 读取边的另一个顶点
                validateVertex(b);

                if (a == b) throw new IllegalArgumentException("Self Loop is Detected!");  // 检测自环边
                // 检测平行边
                if (adj[a].contains(b)) throw new IllegalArgumentException("Parallel Edges are Detected!");

                adj[a].add(b);  // 在a的链表中添加顶点b
                adj[b].add(a);  // 在b的链表中添加顶点a（因为是无向图）
            }
        } catch (FileNotFoundException e) {
            e.printStackTrace();
        }
    }

    /**
     * 验证顶点是否合法
     * @param v 顶点
     */
    private void validateVertex(int v){
        if ( v < 0 && v > V){
            throw new IllegalArgumentException("vertex " + v + " is invalid.");
        }
    }

    /**
     * 获取顶点的度数
     * @param v 顶点
     * @return 顶点的度数
     */
    public int degree(int v){
        return adj(v).size();
    }

    /**
     * 重写toString方法，打印图的信息
     * @return 图的信息字符串
     */
    @Override
    public String toString() {
        StringBuffer stringBuffer = new StringBuffer();
        stringBuffer.append(String.format("V = %d, E = %d\n",V,E));
        for (int i = 0 ; i < V; i ++){
            stringBuffer.append(String.format("%d : ",i));
            for (int w: adj[i]){
                stringBuffer.append(String.format(" %d ", w));
            }
            stringBuffer.append("\n");
        }
        return stringBuffer.toString();
    }

    /**
     * 获取图的顶点数
     * @return 顶点数
     */
    private int V(){
        return V;
    }

    /**
     * 获取图的边数
     * @return 边数
     */
    private int E(){
        return E;
    }

    /**
     * 判断两个顶点之间是否存在边
     * @param v 顶点v
     * @param w 顶点w
     * @return 是否存在边
     */
    public boolean hashEdge(int v, int w){
        validateVertex(v);
        validateVertex(w);
        return adj[v].contains(w);
    }

    /**
     * 获取顶点的邻接链表
     * @param v 顶点
     * @return 邻接链表
     */
    public LinkedList<Integer> adj(int v){
        validateVertex(v);
        return adj[v];
    }

    // 创建AdjList对象，并传入文件名构建邻接表
    public static void main(String[] args) {

        AdjList adjMatrix = new AdjList("g.txt");
        System.out.println(adjMatrix.toString());

    }
}

下面是对各个操作的时间复杂度分析：

空间复杂度：

存储顶点信息：O(V) + 存储边信息：O(E)，即 O(V+E)

时间复杂度：

建图：O(E * V)
查看两点是否相邻：O(deg(v))，其中deg(v)是顶点v的度数，即与顶点v相邻的顶点个数
求一个点的相邻节点：O(deg(v))

11.3 总结

邻接表的空间复杂度相对较低，特别适用于表示稀疏图，因为只存储实际存在的边。

在邻接表中查找两个顶点是否相邻的操作的时间复杂度取决于顶点的度数，平均情况下较为高效。求一个顶点的相邻节点也比较高效，只需要遍历相邻链表即可。

12 优化邻接表

12. 1 提高操作效率

使用哈希表或红黑树可以作为邻接表的优化方式，以提高查询和插入的性能。具体的做法如下：

（1）哈希表

哈希表优化：可以将邻接表中的链表改为哈希表，将顶点映射到对应的链表位置。这样，在查找相邻节点时，可以通过哈希表快速定位到对应的链表，从而提高查询效率。插入新边时，可以利用哈希表的快速插入特性，避免遍历整个链表的操作。

（2）红黑树

红黑树优化：可以将邻接表中的链表改为红黑树，将相邻节点按照顺序插入到红黑树中。这样，在查找相邻节点时，可以通过红黑树的有序性进行二分查找，从而提高查询效率。同时，红黑树支持快速插入和删除操作，可以有效地维护邻接表的动态变化。

12.2 减少空间占用

（1）压缩邻接表

压缩邻接表：对于稀疏图，可以使用压缩存储方式来减少空间占用。例如，使用稀疏矩阵存储边的信息，或者使用邻接表数组结合跳表等数据结构来提高查找性能。

（2）邻接表数组分块

邻接表数组分块：对于大规模图，可以将邻接表数组分块存储，以降低每个链表的长度，减少查找时间。这样可以在牺牲一定空间的情况下提高查询效率。

（3）邻接表数组的排序

邻接表数组的排序：对于频繁的顶点相邻查询，可以考虑对邻接表数组进行排序，以便使用更高效的查找算法，如二分查找。这样可以减少线性查找的时间复杂度。

（4）邻接表的哈希索引

邻接表的哈希索引：使用哈希索引结构加速邻接表的访问，通过哈希函数将顶点映射到对应的链表，提高查找效率。

（5）使用紧凑的数据结构

使用紧凑的数据结构：对于稠密图，可以考虑使用紧凑的数据结构，如邻接矩阵或位图，以减少空间占用并提高访问效率。

12.3 红黑树优化

import java.io.File;
import java.io.FileNotFoundException;
import java.util.LinkedList;
import java.util.Scanner;
import java.util.TreeSet;

/**
 * 邻接表表示图的类
 * @author wushaopei
 * @create 2023-06-02 15:05
 */
public class AdjSet {

    private int V;           // 顶点数
    private int E;           // 边数
    private TreeSet<Integer>[] adj;     // 邻接表

    /**
     * 构造函数，通过读取文件构建邻接表
     * @param fileName 文件名
     */
    public AdjSet(String fileName) {
        // 从文件中读取图的信息
        File file = new File(fileName);
        try (Scanner scanner = new Scanner(file)){
            V = scanner.nextInt();  // 读取顶点数
            if (V < 0 ) throw new IllegalArgumentException("V must be non-negative");
            adj = new TreeSet[V];  // 创建邻接表数组
            for (int i = 0; i < V; i ++){
                adj[i] = new TreeSet<Integer>();  // 初始化邻接表中的每个链表
            }

            E = scanner.nextInt();  // 读取边数
            if (E < 0 ) throw new IllegalArgumentException("V must be non-negative");
            for (int i = 0; i < E; i ++){
                int a = scanner.nextInt();  // 读取边的一个顶点
                validateVertex(a);
                int b = scanner.nextInt();  // 读取边的另一个顶点
                validateVertex(b);

                if (a == b) throw new IllegalArgumentException("Self Loop is Detected!");  // 检测自环边
                // 检测平行边
                if (adj[a].contains(b)) throw new IllegalArgumentException("Parallel Edges are Detected!");

                adj[a].add(b);  // 在a的链表中添加顶点b
                adj[b].add(a);  // 在b的链表中添加顶点a（因为是无向图）
            }
        } catch (FileNotFoundException e) {
            e.printStackTrace();
        }
    }

    /**
     * 验证顶点是否合法
     * @param v 顶点
     */
    private void validateVertex(int v){
        if ( v < 0 && v > V){
            throw new IllegalArgumentException("vertex " + v + " is invalid.");
        }
    }

    /**
     * 获取顶点的度数
     * @param v 顶点
     * @return 顶点的度数
     */
    public int degree(int v){
        validateVertex(v);
        return adj[v].size();
    }

    /**
     * 重写toString方法，打印图的信息
     * @return 图的信息字符串
     */
    @Override
    public String toString() {
        StringBuffer stringBuffer = new StringBuffer();
        stringBuffer.append(String.format("V = %d, E = %d\n",V,E));
        for (int i = 0 ; i < V; i ++){
            stringBuffer.append(String.format("%d : ",i));
            for (int w: adj[i]){
                stringBuffer.append(String.format(" %d ", w));
            }
            stringBuffer.append("\n");
        }
        return stringBuffer.toString();
    }

    /**
     * 获取图的顶点数
     * @return 顶点数
     */
    private int V(){
        return V;
    }

    /**
     * 获取图的边数
     * @return 边数
     */
    private int E(){
        return E;
    }

    /**
     * 判断两个顶点之间是否存在边
     * @param v 顶点v
     * @param w 顶点w
     * @return 是否存在边
     */
    public boolean hashEdge(int v, int w){
        validateVertex(v);
        validateVertex(w);
        return adj[v].contains(w);
    }

    /**
     * 获取顶点的邻接链表
     * @param v 顶点
     * @return 邻接链表
     */
    public Iterable<Integer> adj(int v){
        validateVertex(v);
        return adj[v];
    }

    // 创建AdjList对象，并传入文件名构建邻接表
    public static void main(String[] args) {

        AdjSet adjMatrix = new AdjSet("g.txt");
        System.out.println(adjMatrix.toString());
        System.out.println(adjMatrix.adj(1));
    }
}

12.4 图的基本表示的比较

	空间	建图时间	查看两点是否相邻	查找点的所有临边
邻接矩阵	O(V^2)	O(E)	O(1)	O(V)
邻接表（LinkedList）	O(V + E)	O(E) 如果查重：O(E * V)	O(degree(v)) O(v)	O(degree(v)) O(V）文章来源地址https://www.toymoban.com/news/detail-766204.html
邻接表（TreeSet）	O(V + E)	O(ElogV)	O(logV)	O(degree(v)) O(V）