前言
本人水平有限,文章仅作为自己的学习记录,且多用不严谨的、通俗易懂的语言去介绍。如有错误,希望大佬们多多批评指正。
系列文章01——记录我对傅里叶级数的理解和学习过程
一、由周期矩形脉冲信号引入傅里叶变换
1.1初识傅里叶变换

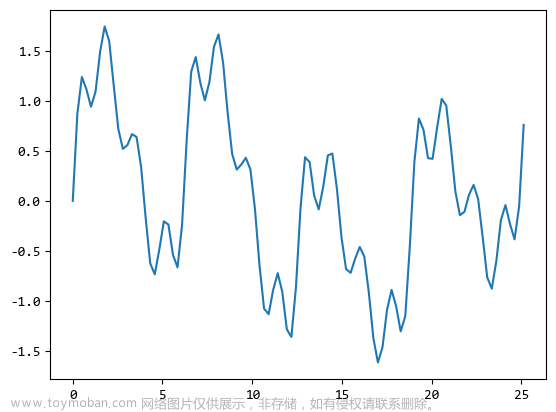
如上图(左)所示,时域f(t)为一个周期信号,在上一讲中,我们学习了傅里叶级数,可以对它求复指数形式的傅里叶级数展开,其中cn为离散的幅度谱。
如上图(右)所示,横轴为频率轴,纵轴为幅值,称为幅度谱。但是这些不统一的符号让我们看的很烦,因此我们懂得原理之后,将傅里叶级数的符号改一下,如下图所示。

现在我们换个说法,把傅里叶级数中提到的幅度谱换成频谱。实际意义不改变,仍然是横轴为频率轴w,为基频w0、2w0....kw0等频点,对应的位置,纵轴为幅度F(kw0)。
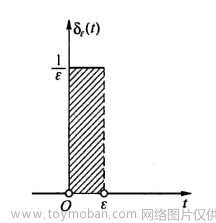
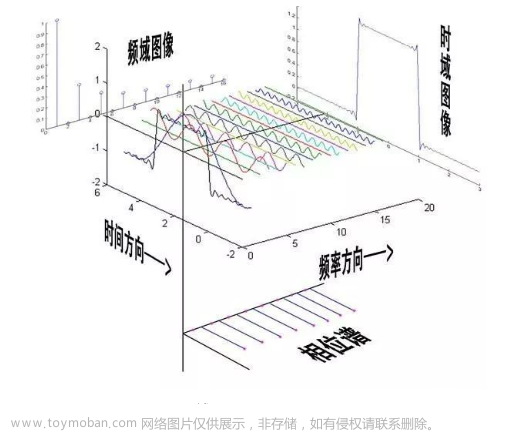
现在来想一个问题,增大周期脉冲信号的周期T,F(kw0)频谱怎么变?那一根一根的谱线,是变宽还是变密呢?

很显然,变密了!再继续增大f(t)的周期T,极限一点,直接增大到T无穷大,F(kw0)怎么变?

答曰:频谱似乎变成了一个连续谱!
1.2总结
总结:我们先对f(t)进行傅里叶级数展开看到一根一根线,并且将幅度谱换了个说法,引入了频谱的概念。紧接着增大f(t)的周期,我们发现频谱变密直到变成了一个连续的样子。
学过信号与系统的朋友们应该知道一个结论:时域连续、周期,频域非周期、离散;时域连续、非周期,频域非周期、连续。所以把傅里叶级数所学的概念推广一下,如果要研究一个连续、非周期信号,我们可以采用傅里叶变换的方法去分析一个信号的频率成分!
二、傅里叶变换公式学习
2.1公式推导
上文举了一个周期矩形脉冲的例子,通过增大T,形象地看了一下频谱的变化,初识傅里叶变换。现在通过公式推导,引出傅里叶变换公式。

如上图所示,画五角星的地方,就是傅里叶正变换公式。我的推导式不严谨的、错误的,但是可以方便理解。
2.2频谱密度的概念理解
在上面的推导中,把(2*pi/w0)*F(kw0)这么一长串式子写作了F(w),为了最终这个F(w)有意义,我们在一开始的时候,就对等式两边同时乘了周期T0。因为按照傅里叶级数公式去推导,T0增大,有可能那个幅度谱的幅度会变成0。正因为这样,我们把最后表示出来的F(w)又取了一个新名字,叫频谱密度。
刚开始学习的时候,我把傅里叶级数系数画出来的图叫幅度谱,把傅里叶变换画出来的图叫频谱密度,现在我会统称为频谱,因为我反正是要弄清楚一个信号的频率成分是什么,它们都是以频率为横轴的图像,那就统称频谱吧!
2.3由傅里叶变换发散出的一些思考
2.3.1什么是调制?工作中常说的基带和射频是什么?频谱搬移发生在哪个过程?
这篇文章普及基带和射频。
常说的基带和射频是指什么?
我在本科期间参加过电赛,当时有学习如何将信号发生器给进来的低频信号,经过调制用天线发射出去,最后再接收回来经过解调复原。现在和当时一样脑子嗡嗡的,啥也不懂,通信原理也没学好,当时脑子里留下的调制概念,就分为数字调制和模拟调制。
殊不知,在当今通信领域,调制=基带调制+射频调制,这样理解会更贴近生活。推荐看一下这篇文章,像我这样基础差的,也可以很清晰的知道个大概框架。
关于信号调制的基本概念(基带调制vs射频调制)
看完这两篇文章之后,为了方便我自己的理解,斗胆答曰:现代意义上的调制是指基带调制(不发生频谱搬移,通原书上的数字调制)和射频调制(就是通信原理书中学的模拟调制)。
2.3.2傅里叶变换和频谱搬移
梳理一下逻辑,本文初识了傅里叶变换,对信号作傅里叶变换后看到了一个连续频谱;然后分享了两篇文章,知道了通信中基带和射频的概念,以及调制的概念;最后我们记录一下傅里叶变换和频谱搬移的关系。运用一下傅里叶变换公式+时域/频域卷积定理。

如上图可以看见,基带处理后的信号s(t)分析其频率成分,作傅里叶变换频谱为S(w);射频部分要对它进行频谱搬移,调制到更高的频段,已调信号为SRF(t),对应频谱为SRF(w),实际上就是S(w)的频谱搬移到了wc处,达到了调制到更高频段的目的。文章来源:https://www.toymoban.com/news/detail-766223.html
2.3.3关于复指数信号的思考
继续埋坑文章来源地址https://www.toymoban.com/news/detail-766223.html
到了这里,关于记录我对傅里叶变换的理解和学习过程的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!