连续体机器人的正逆向运动学模型-（4）雅可比矩阵解决逆向运动

8月前作者：LJL_hhh 分类：Toy博客阅读(28) 违法举报

这篇具有很好参考价值的文章主要介绍了连续体机器人的正逆向运动学模型-（4）雅可比矩阵解决逆向运动。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

章节分布

Winter：连续体机器人的正逆向运动学模型-（1）概述
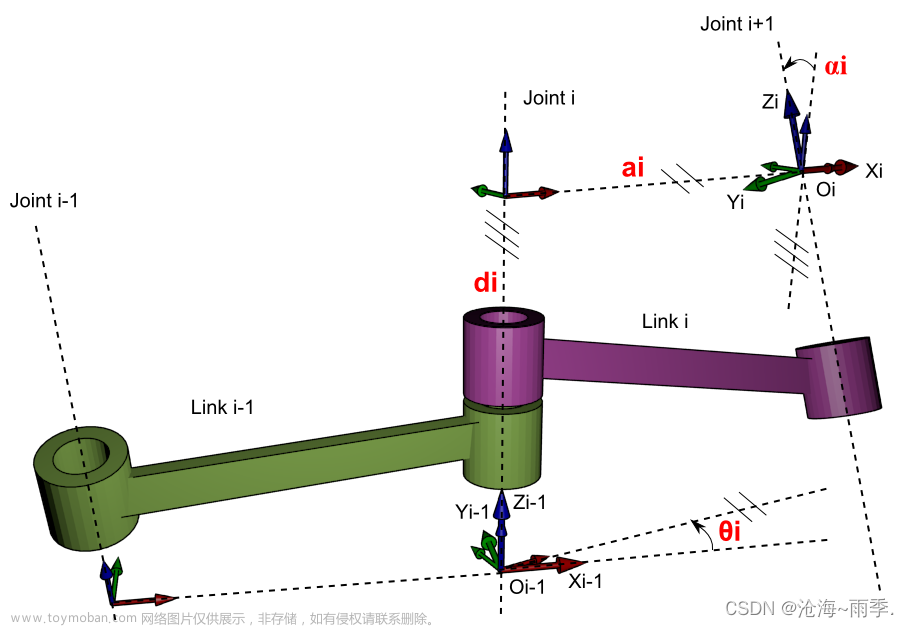
Winter：连续体机器人的正逆向运动学模型-（2）DH参数法与雅可比矩阵
Winter：连续体机器人的正逆向运动学模型-（3）利用DH参数法解决正向运动学
连续体机器人的正逆向运动学模型-（4）雅可比矩阵解决逆向运动 - 知乎

参考资料

《Robot Modeling and Control》 by Mark W. Spong

Design and Kinematic Modeling of Constant Curvature Continuum Robots: A Review

注：还会发布其他机器人运动学知识，欢迎关注

回顾雅可比矩阵 jacobian

1.意义：干嘛的

连续机器人运动学建模的几何分析法,机器人,矩阵,人工智能

指公式中的J

广义上的雅克比矩阵，其实就是一个偏导数组成的矩阵

而在机器人领域，可以看上面的公式，公式的右侧q就是关节的速度，公式的左侧就是末端执行器的速度，

而雅克比矩阵在这个过程中就是起一个作用，给定一个关节的速度，我就可以得到末端执行器的速度，那么这个雅可比矩阵，我们也可以联想到是跟机器人的位姿有关系的，就是这个机器人是怎么摆放的。

而这个机器人怎么摆放决定了我们安放的坐标系，以及我们得到的DH参数表，这些我们在第三节已经得到

而不论是传统的机器人还是连续体机器人，只要你得到了DH参数表，接下来的步骤就是一样的

2.怎么得到

对于旋转关节

连续机器人运动学建模的几何分析法,机器人,矩阵,人工智能 — 标旋转关节的jacobian

对于移动关节

连续机器人运动学建模的几何分析法,机器人,矩阵,人工智能 — 标移动关节

第二篇文章有对应的例子和答案，很简洁可以检查一下自己是否理解，链接如下

Winter：连续体机器人的正逆向运动学模型-（2）DH参数法与雅可比矩阵

逆向运动的迭代公式

连续机器人运动学建模的几何分析法,机器人,矩阵,人工智能

1.公式解读

来源：这个公式很明显是由第1个公式进行离散化得到的

就是机器人的关节角度，通过不断的迭代，就可以得到新的关节角度

就是雅可比矩阵的逆矩阵，对应于时候的形态，当然这里有一点讲究，下面会说

Δt 就是步长了

v()是末端操纵器的速度，包括线速度和角速度，涉及两个公式

连续机器人运动学建模的几何分析法,机器人,矩阵,人工智能

连续机器人运动学建模的几何分析法,机器人,矩阵,人工智能

2.遇到自由度不为6的时候（冗余/驱动不足）

刚刚提到在这个迭代公式里面，雅可比矩阵是需要求逆的，雅可比矩阵一定是六行的，但是它的列数取决于关节的数量，如果关节恰好等于6，那么是可以求逆的，如果在不等于6的情况下，应该怎么办呢？

如果关节数n小于6 雅可比就是 6 X n 就需要看雅可比矩阵的秩

连续机器人运动学建模的几何分析法,机器人,矩阵,人工智能

此时就有一个解

如果关节数n大于6 ，就有可能出现多解的情况，使用它的伪逆矩阵

需要一些线代方面的知识

对于 J ∈R m×n，如果m<n且秩 J =m，则存在。

连续机器人运动学建模的几何分析法,机器人,矩阵,人工智能

可以看到伪逆矩阵为

文章来源地址https://www.toymoban.com/news/detail-766359.html

对应MATLAB中的

J_pinv = pinv( J_double );

这样可以得到接下来两个公式

连续机器人运动学建模的几何分析法,机器人,矩阵,人工智能

这个b是任意的，通过下面的公式可以看到并不影响，b会消失

连续机器人运动学建模的几何分析法,机器人,矩阵,人工智能

展示逆向运动

给定一个目标位置姿态进行迭代

连续机器人运动学建模的几何分析法,机器人,矩阵,人工智能

到了这里，关于连续体机器人的正逆向运动学模型-（4）雅可比矩阵解决逆向运动的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：

领支付宝红包赞助服务器费用

机器人学基础（三）：机器人运动学

运动学问题是在不考虑引起运动的力和力矩的情况下，描述机械臂的运动。上一篇我们已经讨论了机器人运动方程的表示方法，这一篇将会讨论机器人的DH建模方法。 Denavit-Hartenberg（D-H）模型于1955年首次提出，用于描述机器人连杆和节点之间相互关系。后来逐步完善推导出了

2024年02月09日
浏览(37)
工业机器人（六）——运动学分析

Delta 并联机构具有工作空间大、运动耦合弱、力控制容易和工作速度快等优点，能够实现货物抓取、分拣以及搬运等，在食品、医疗和电子等行业中具有广泛的应用。在结构设计的基础上，本部分通过运动学和动力学分析，为并联机构优化设计提供前期基础，具体内容如

2024年02月09日
浏览(33)
基于C#的机器人仿真平台和机器人运动学算法实现

一、平台搭建 1.利用wpf自带的库进行机器人各关节导入相关代码段：导入效果如图：效果视频： 2.通过正运动学显示机器人当前位置信息拖动机器人并且实时改变其位置信息： xaml代码部分：算法部分： 3.功能实现（在X/Y/Z轴上设置一个移动距离，然后机器人自动移动该

2024年02月16日
浏览(36)
机器人运动学标定：基于DH建模方法

作者：桂凯链接：https://www.zhihu.com/question/401957723/answer/1298513878 来源：知乎著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。当然，运动学标定这种很基础的问题，理论已非常成熟了，基于激光或拉线编码器的标定系统也已经商业化了。我们在接

2024年02月12日
浏览(39)
六自由度机器人（机械臂）运动学建模及运动规划系列（一）——简介

毕业设计做了六轴机器人相关的课题，做完之后学到很多，在这里分享一下。本篇首先对六轴机器人及其研究内容进行简单的介绍。六轴机器人中的六轴指个六自由度，由关节和连杆组成。常见的六轴机器人为串联型旋转关节机器人。这里以一款川崎机器人为例，展示一下

2024年02月02日
浏览(34)
机器人运动学——轮速里程计（SLAM）

目录一、机器人运动学分析二、阿克曼小车 2.1运动学分析想要让机器人运动，除了提供目标速度还不够，需要将机器人的目标速度转换每个电机实际的目标速度，最终根据电机的目标速度对电机的控制实现对机器人的控制。机器人的目标速度转换成电机的目标速度这

2024年02月16日
浏览(27)
六自由度机器人（机械臂）运动学建模及运动规划系列（四）——轨迹规划

对机器人进行轨迹规划的主要任务是，根据机器人的工作环境和工作任务要求，求得一系列机器人末端位姿变换的时间序列，使得机器人末端可以正确地从初始姿态沿着期望的轨迹运动到终止位姿，完成工作任务，。对于六自由度的机器人来说，轨迹规划要解决的关键问题是

2024年02月03日
浏览(56)
雅克比矩阵在机器人运动学中的应用

以六轴机械臂为例，设机械臂关节空间为q，位置矩阵为p，速度矩阵为v q = [ q 0 , q 1 , q 2 , q 3 , q 4 , q 5 ] q=[q_0,q_1,q_2,q_3,q_4,q_5] q = [ q 0 , q 1 , q 2 , q 3 , q 4 , q 5 ] p = [ x , y , z ] T = [ f x ( q ) f y ( q ) f z ( q ) ] p=[x,y,z]^T=begin{bmatrix}f_x(q) \\\\ f_y(q)\\\\ f_z(q) \\\\ end{bmatrix} p =

2024年02月13日
浏览(30)
双足机器人Cassie运动学和动力学计算

官方要求的运行环境：我的环境： (1)Matlab2023b (2)Mathematica12.3.1 (3)MEX和FROST的安装可参考我上一篇文章 Windows下安装动力学仿真软件Frost-CSDN博客 https://blog.csdn.net/SWORDHOLDER/article/details/137511000?spm=1001.2014.3001.5502 下载地址(有时候访问比较慢则需要魔法) GitHub - UMich-BipedLab/Cassie

2024年04月14日
浏览(40)
机器人逆运动学求解——矢量积法计算雅可比矩阵

雅可比矩阵：机器人操作空间速度与关节空间速度的线性映射关系，可以视作从关节空间向操作空间运动速度的传动比。令机械手的运动方程为：表示操作空间与关节空间的位移关系则两边同时对时间求导，就可以求解出q与x之间

2024年04月27日
浏览(26)