有向无环图的拓扑排序理解和算法-Toy模板网

这篇具有很好参考价值的文章主要介绍了有向无环图的拓扑排序理解和算法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

有向无环图的拓扑排序理解和算法

有向无环图(DAG)定义

引用子维基百科的DAG定义, 在数学中，尤其是图论和计算机科学中，DAG是一类不含环的有向图(In mathematics, particularly graph theory, and computer science, a directed acyclic graph (DAG) is a directed graph with no directed cycles). 对比之前的有向图的强连通分量，凡是在图中能能够找到强连通分量的有向图（单个顶点除外），都排除在DAG之外。对于有向无环图，拓扑排序是其关键的操作，通过拓扑排序，便能把有向无环图的先后遍历顺序”线性化“。

DAG的应用

现实世界中，很多场合都涉及到DAG的应用，最常见的应用包括，项目管理中各个事件先后顺序排列的可行性，学校选课系统设计, 程序设计的互相依附以及事件的模拟等等。

我们以某高校的选课系统为例进行说明，如果要选择Class H, 那么选修之前需要完成Class D 和 Class E课程，如果要选择Class D课程，就需要提前学习Class A和 Class B.

有向无环,算法,图论

选择Class H的前置条件

有向无环,算法,图论

拓扑排序目标

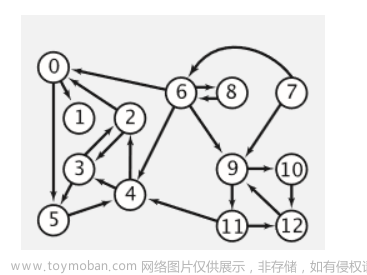
在拓扑排序中，我们需要对有向无环图每个顶点进行检查，经过拓扑排序后，我们会形成一个类似数组的线性结构来表示各个顶点的先后顺序，Dynamic Programming就需要利用DAG形成某些节点，对这些节点进行共用，减少计算事件。值得一提的是，拓扑排序的结果不一定唯一，同一个DAG图形可能会有几个不同的拓扑排序。我们以下图为例，

有向无环,算法,图论

最后形成的线性次序关系如下：
有向无环,算法,图论

算法原理

一般实现Topological 排序方法有 Kahn’s 算法和 DFS算法，

Kahn’s 算法非常直观，两步循环即可

(1)在有向图中选一个没有前驱的顶点且输出之

(2)在图中删除该顶点和所有以它为尾的弧，换言之；对于图上以此点为弧头的顶点，其入度减1

重复上述两步，直至全部顶点均已输出，或者当前图中不存在无前驱的顶点为止（存在环)

在Kahn’s 算法中：

(a)可以直接线性搜索入度为0的顶点（没有前驱)

(b) 利用栈或队列进行保留入度为0的顶点，后面直接出栈，更新相关顶点的入度值

两类算法的事件复杂度分别为O(|V|2)和O(|V|+|E|).

DFS 算法当有向图中无环时，也可用DFS进行拓扑排序，因为图中无环，则由图中某点出发进行深度优先搜索遍历时，最先退出DFS函数的顶点即出度为零的顶点，是拓扑有序序列中的最后一个顶点。可以利用数组进行拓扑有序序列中的序号存储。

© DFS算法实现

算法代码实现

(a)可以直接线性搜索入度为0的顶点（没有前驱)

/**
	Use Adajacent list to go through each vertex
	Work out the indegree array based on the traversal
*/
void assign_indegree(ALGraph G, int *indegree)
{
    int i;
    int v;
    int w;

    
    for(v=0;v<G.vexnum;v++)
    {
        for(w=FirstAdjVex(G,v);w>=0;w=NextAdjVex(G,v,w))
        {
            indegree[w]++;
        }
    }    
}

/**
Linear search the indegree array and return the first new zero indegree vertex node
*/
int find_new_zero_indegree_vertex(ALGraph G, int *indegree, int *top_num)
{
    int i;

    for(i=0;i<G.vexnum;i++)
    {
        if(top_num[i]==-1 && indegree[i]==0)
        {
            return i;
        }
    }

    return NOT_A_VERTEX;  //NOT_A_VERTEX=-1；
}

/**
	Find the topological sort of directed graph
*/
Status topological_sort(ALGraph G,void (*visit)(VertexType e))
{
    int counter;
    int indegree[MAX_VERTEX_NUM];
    int top_num[MAX_VERTEX_NUM]; //top_num will store the top order vertex #No.
    int v;
    int w;

    for(counter=0;counter<G.vexnum;counter++)
    {
        *(top_num+counter)=-1;
    }

    memset(indegree,0,sizeof(int)*MAX_VERTEX_NUM);
    assign_indegree(G,indegree);

    for(counter=0;counter<G.vexnum;counter++)
    {
        v=find_new_zero_indegree_vertex(G,indegree,top_num);

        //If v equals to NOT Available VERTEX, 
        //it must contain the cycle in the graph
        //terminate the program
        if(v==NOT_A_VERTEX)
        {
            return ERROR;
        }
		
        
        *(top_num+v)=counter;

        for(w=FirstAdjVex(G,v);w>=0;w=NextAdjVex(G,v,w))
        {
            indegree[w]--;
        }
    }

    dispay_order(G,top_num,visit);
}

/**
Display the topological order based on top_num array list
*/
void dispay_order(ALGraph G, int *top_num, void (*visit)(VertexType e))
{
    int i;

    for(i=0;i<G.vexnum;i++)
    {
        visit(G.vertices[top_num[i]].data);
    }
}

(b) 利用栈或队列进行保留入度为0的顶点，后面直接出栈，更新相关顶点的入度值

void assign_indegree(ALGraph G, int *indegree)
{
    int i;
    int v;
    int w;

    
    for(v=0;v<G.vexnum;v++)
    {
        for(w=FirstAdjVex(G,v);w>=0;w=NextAdjVex(G,v,w))
        {
            indegree[w]++;
        }
    }    
}

Status topological_sort(ALGraph G,void (*visit)(VertexType e))
{
    SqStack S;
    int indegree[MAX_VERTEX_NUM];
    int i;
    int v;
    int w;
    int count;

    InitStack_Sq(&S);
    memset(indegree,0,sizeof(int)*MAX_VERTEX_NUM);
    assign_indegree(G,indegree);
    count =0;

    for(i=0;i<G.vexnum;i++)
    {
        if(!indegree[i])
        {
            Push_Sq(&S,i);
        }
    }

    while(!StackEmpty_Sq(S))
    {
        Pop_Sq(&S,&v);
        visit(G.vertices[v].data);
        count++;

        for(w=FirstAdjVex(G,v);w>=0;w=NextAdjVex(G,v,w))
        {
            if(!(--indegree[w]))
            {
                Push_Sq(&S,w);
            }
        }
    }

    if(count<G.vexnum)
    {
        return ERROR;
    }

    return OK;


}

Status find_topological_sort(ALGraph G, int *ordering)
{
    int v;
    int w;
    count =0;
    int index;
    memset(visited,0,sizeof(int)*MAX_VERTEX_NUM);
    index=G.vexnum-1;

    for(v=0;v<G.vexnum;v++)
    {
        if(!visited[v])
        {
            dfs_topological_sort(G,v,index-count,ordering);
        }
    }

    if(count<G.vexnum)
    {
        return ERROR;
    }

    return OK;
}

//----
int dfs_topological_sort(ALGraph G, int v0, int index, int *ordering)
{
    
    int v;
    int w;
    visited[v0]=1;
    count++;

    v=v0;

    for(w=FirstAdjVex(G,v);w>=0;w=NextAdjVex(G,v,w))
    {
         if(!visited[w])
        {
            //index will be kept as the same as DFS deep dive into search
            //when the first recursive call ended, it will be decremented by 1
            //and in the next loop, index will be upated in the recursive call
            index=dfs_topological_sort(G,w,index,ordering);
        }
    }
    
    ordering[index]=v;
    return index-1;
}
//------
void dispay_ordering(int *ordering, ALGraph G, void (*visit)(VertexType e))
{
    int i;

    for(i=0;i<G.vexnum;i++)
    {
        visit(G.vertices[ordering[i]].data);
    }
}