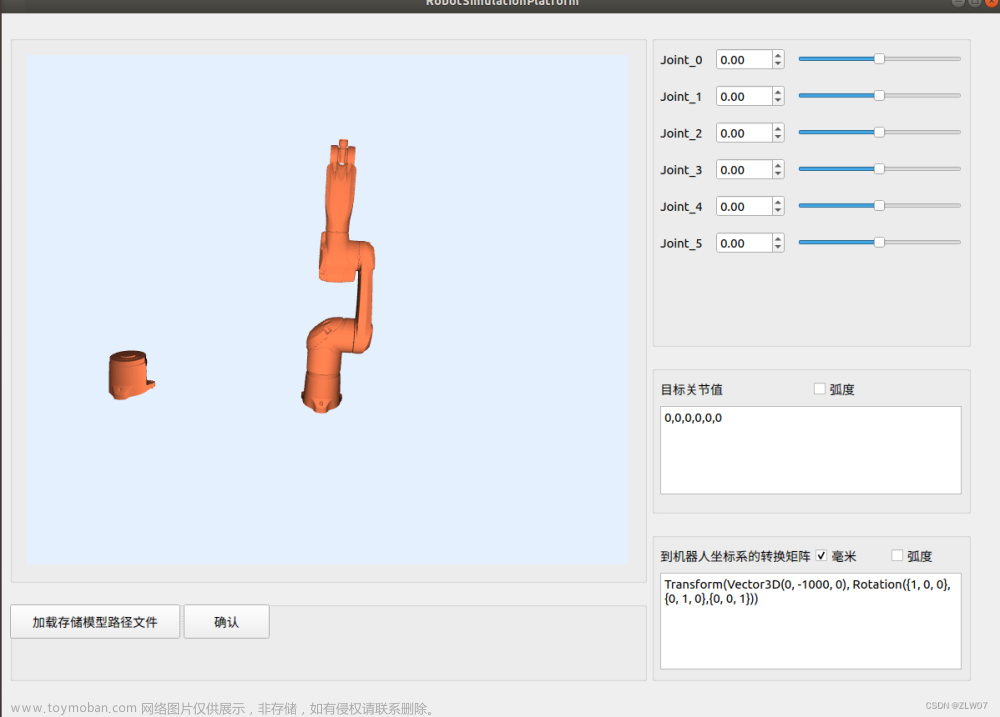
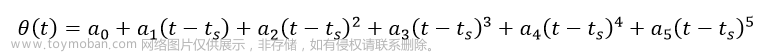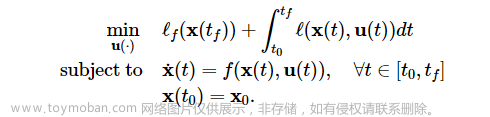机器人建模辨识控制——柔性运动控制-Toy模板网

这篇具有很好参考价值的文章主要介绍了机器人建模辨识控制——柔性运动控制。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

《Modeling Identification and control of robots》
Chapter15 compliant motion control 柔性运动控制

中间会穿插一些前面的知识作为补充，具体均在目录中体现，原书中有错误的地方也均在本文中体现

14.3.1 关节空间中的PID控制

$\tau=K_p(q_d-q)+K_d(\dot{q}_d-\dot{q})+{K_i}\int_{t_0}^1(q_d-q)d\tau\tag{1}$
机器人建模辨识控制——柔性运动控制,机器人,机器人,人工智能

14.3.3 任务空间中的PID控制

当机器人在任务空间（笛卡尔空间）中的运动轨迹已经明确时，可以采用以下两种方法来构建控制系统：

在任务空间task space中设计控制方法；
将任务空间中的指定轨迹转换为关节空间中的轨迹，然后在关节空间中进行控制。

机器人建模辨识控制——柔性运动控制,机器人,机器人,人工智能

根据上图，为获得关节空间中的力矩 $\tau$ ，需要将(1)中的q替换为x，得到任务空间中的F，由于 $\tau={J^T}F$ ，需再左乘 $J^T$ 得到关节空间中的 $\tau$ ，因此有：
$\tau=J^T[K_p(x_d-x)+K_d(\dot{x}_d-\dot{x})+{K_i}\int_{t_0}^1(x_d-x)d\tau] \tag{2}$
将任务空间的期望轨迹转换为关节空间的期望角度有两种方法，一是通过正运动学计算出关节位置再微分计算关节速度和加速度，二是计算关节位置，速度，加速度如下：

关节位置

$q_d=F.K.(x_d)$
关节速度

$\dot{x}_d=J(q_d)\dot{q}_d$

$\dot{q}_d=J(q_d)^{-1}\dot{x}_d$
关节加速度

$\ddot{x}_d=\dot{J}\dot{q}_d+{J}\ddot{q}_d$

$\ddot{q}_d={J}^{-1}(\ddot{x}_d-\dot{J}\dot{q}_d)$

14.4 线性解耦控制

14.4.1 介绍

线性化和解耦技术是利用适当的反馈规律将非线性控制问题转化为线性控制问题

14.4.2 在关节空间中计算力矩控制

假设关节的位置和速度是可测量的并且测量结果是无噪声的。设 $\hat{A}$ 和 $\hat{H}$ 分别为A和H的估计。因此控制力矩可写为：
$\tau=\hat{A}(q)w(t)+\hat{H}(q,\dot{q})$
推导出在建模完美且不存在干扰的理想情况下，问题简化为n个解耦双积分器的线性控制问题。 $\ddot{q}=w(t)$ 是新的输入控制向量。

注：机器人动力学模型的一般形式为：
$\tau=A(q)\ddot{q}+C(q,\dot{q})\dot{q}+Q(q)+diag(\dot{q})F_v+diag(sign(\dot{q}))F_c$
更简明的形式为：
$\tau=A(q)\ddot{q}+H(q,\dot{q})\tag{3}$

14.4.3 在任务空间中计算力矩控制

任务空间中的动态控制也称为分解加速度控制，把(3)中的 $\ddot{q}$ 替换掉：
$\tau=A {J^{-1}}(\ddot{X}-\dot{J}\dot{q})+H$
对任务空间中的方程进行求解和解耦的控制方法表述为：
$\tau=\hat{A} {J^{-1}}(w(t)-\dot{J}\dot{q})+\hat{H}$

15 柔性运动控制

15.3 被动刚性控制

15.4 主动刚性控制

$^cf_c=K_c\ ^cdX_c\\ \tau=J^Tf\\ dX=Jdq\\\tau=J^TK_cJdq=K_q dq$

矩阵 $K_q$ 称为关节刚度矩阵，它不是对角矩阵而是对称的。它决定了伺服回路在关节空间中的比例增益。它与运动学模型的雅可比矩阵具有相同的奇异位置，这意味着，对于这些构型，我们无法在柔度框架的所有自由度上或周围获得所需的刚度。所以可以将模型更新如下：

机器人建模辨识控制——柔性运动控制,机器人,机器人,人工智能

$\tau=K_q(q^d-q)+K_d(\dot{q}^d-\dot{q})+Q$
Q代表重力补偿， $K_d$ 可被理解为阻尼矩阵，如果在某个方向上需要纯力控制，可以 $\tau=J^Tf$ 添加前馈力。

这种主动刚性控制的优点是执行起来相对简单，因为刚度矩阵可以在线更改，以使机器人的行为适应各种任务约束。

15.5 阻抗控制

阻抗控制的基本思想是当机器人的效应器与环境相互作用时，赋予机器人一个规定的动态行为。期望的性能由表示质量-弹簧-阻尼系统的广义动态阻抗指定。

机器人阻抗Z根据任务的不同阶段而变化。通常，将机器人等效为一个质量-弹簧-阻尼器二阶系统，其传递函数为:
$sZ(s)=Ms^2+Bs+K$

M给高值可以限制机器人动力学，加速度越小，状态越难改变
在需要耗散动能从而抑制响应的方向上给予B高值
刚度K影响位置控制的精度:沿力控制方向，刚度应足够小以限制接触力;相反，在位置控制方向上，用户应设置较高的刚度以获得末端执行器的精确定位。

根据有无力传感器，可以将阻抗控制框图分为两种形式：

无力传感器反馈

机器人建模辨识控制——柔性运动控制,机器人,机器人,人工智能

有力传感器反馈

机器人建模辨识控制——柔性运动控制,机器人,机器人,人工智能

15.5.1 无力传感器的阻抗控制

机器人建模辨识控制——柔性运动控制,机器人,机器人,人工智能

无力传感器反馈的阻抗控制方案，相当于任务空间中的PD控制(14.3.3)

$\tau=J^{\mathrm{T}}\left[\mathbf{B}\left(\mathbf{\dot{X}}^\mathrm{d}-\mathbf{\dot{X}}\right)+\mathbf{K}\left(\mathbf{X}^\mathrm{d}-\mathbf{X}\right)\right]+\mathbf{Q}$

K矩阵和B矩阵包含任务空间中的比例增益和导数（微分）增益，可以分别解释为机器人的刚度矩阵和阻尼矩阵。矢量Q表示重力扭矩补偿。

15.5.2 有传感器的阻抗力控

当机器人和环境接触时施加于环境的接触力向量为 $F_e$ 时， $F_e$ 一般为 $6\times1$ 的力与力矩向量，机器人的动力学模型为
(the dynamic model of a robot exerting a wrench $F_e$ on its
environment)：
$\tau=A(q)\ddot{q}+C(q,\dot{q})\dot{q}+Q(q)+J^TF_e$
期望的接触力：
$F_e=\Lambda\left(\ddot{{X}}^{d}-\ddot{{X}}\right)+\mathrm{B}\left(\dot{{X}}^{d}-\dot{{X}}\right)+\mathrm{K}\left(X^{d}-X\right)$
可以推导出：
$\ddot{X}(t)=\ddot{X}^d+\Lambda^{-1}\left[B\left(\dot{X}^d-\dot{X}\right)+K\left(X^d-X\right)-F_e\right]$
其中， $X^d(t)$ 是期望轨迹位置， $X (t)$ 是实际位置。

把在关节空间表达的动力学方程转换为在任务空间中表达，即将其中的 $q$ 用x代替，又有 $\ddot{q}={J}^{-1}(\ddot{x}-\dot{J}\dot{q})$ 和 $\dot{q}=J(q)^{-1}\dot{x}$ ，则推导过程如下：
$\begin{aligned} J^{-T}\tau&=J^{-T}A(q)\ddot{q}+J^{-T}C(q,\dot{q})\dot{q}+J^{-T}Q(q)+F_e\\ &=J^{-T}A(q)({J}^{-1}(\ddot{x}-\dot{J}\dot{q}))+J^{-T}C(q,\dot{q})\dot{q}+J^{-T}Q(q)+F_e\\ &=J^{-T}A(q){J}^{-1}\ddot{x}-J^{-T}A(q){J}^{-1}\dot{J}\dot{q}+J^{-T}C(q,\dot{q})\dot{q}+J^{-T}Q(q)+F_e\\ &=J^{-T}A(q){J}^{-1}\ddot{x}+(J^{-T}C(q,\dot{q})-J^{-T}A(q){J}^{-1}\dot{J})\dot{q}+J^{-T}Q(q)+F_e\\ &=J^{-T}A(q){J}^{-1}\ddot{x}+(J^{-T}C(q,\dot{q})-J^{-T}A(q){J}^{-1}\dot{J})J^{-1}\dot{x}+J^{-T}Q(q)+F_e\\ &=J^{-T}A(q){J}^{-1}\ddot{x}+(J^{-T}C(q,\dot{q})J^{-1}-J^{-T}A(q){J}^{-1}\dot{J}J^{-1})\dot{x}+J^{-T}Q(q)+F_e\\ \end{aligned}$
可写作;
$J^{-T}\tau=A_x(q)\ddot{X}+C_x(q,\dot{q})\dot{X}+Q_x(q)+F_e$
其中，

$A_x(q)=J^{-T}A(q){J}^{-1}$ 是任务空间中的惯性矩阵
$C_x(q,\dot{q})=J^{-T}C(q,\dot{q})J^{-1}-J^{-T}A(q){J}^{-1}\dot{J}J^{-1}=J^{-T}C(q,\dot{q})J^{-1}-A_x(q)\dot{J}J^{-1}$ 是科里奥利力矩和离心力矩在任务空间中的表达
$Q_x(q)=J^{-T}Q(q)$ 是任务空间中的重力矩
书中有误，这里是有力传感器的阻抗控制

因此用 $w (t)$ 代替 $\ddot{X}$ ，解耦控制有：
$\begin{aligned} \tau &=J^{T}[\hat{A}_x(q)w(t)+\hat{C}_x(q,\dot{q})\dot{X}+\hat{Q}_x(q)+F_e]\\ &=J^{T}\hat{A}_x(q)\{\ddot{X}^d+\Lambda^{-1}[B(\dot{X}^d-\dot{X})+K\left(X^d-X\right)-F_e]\}+\\ & J^{T}\hat{C}_x(q,\dot{q})\dot{X}+J^{T}\hat{Q}_x(q)+J^{T}F_e\\ &=J^{T}\hat{A}_x(q)\{\ddot{X}^d+\Lambda^{-1}[B(\dot{X}^d-\dot{X})+K\left(X^d-X\right)]\}+\\ & J^{T}(\hat{C}_x(q,\dot{q})\dot{X}+\hat{Q}_x(q)+F_e-\hat{A}_x(q)\Lambda^{-1}F_e)\\ &=J^{T}\hat{A}_x(q)\{\ddot{X}^d+\Lambda^{-1}[B(\dot{X}^d-\dot{X})+K\left(X^d-X\right)]\}+\\ & J^{T}[\hat{C}_x(q,\dot{q})\dot{X}+\hat{Q}_x(q)+(I-\hat{A}_x(q)\Lambda^{-1})F_e]\\ \end{aligned}$
如果如果在准静态情况下，因为机械臂末端与环境直接接触，速度近似为零，这里我们认为速度为0， $\dot{J}$ 和 $\hat{C}(q,\dot{q})\dot{X}$ 被认为是零矩阵，因为实际控制过程中科里奥利力矩阵计算量很大，上式可以改写为：
$\tau=J^{T}\hat{A}_x(q)\Lambda^{-1}[\Lambda\ddot{X}^d+B(\dot{X}^d-\dot{X})+K\left(X^d-X\right)-F_e]+{Q}_x(q)+J^TF_e$
这里 $F_e$ 出现了两次

$J^TF_e$ 补偿机器人施加的外部力矩
$-J^T\hat{A}_x\Lambda^{-1}F_e$ 表示增益为 $-J^T\hat{A}_x\Lambda^{-1}$ 的力反馈

而且，如果 $\Lambda=A_x(q)$ ，那么包含 $F_e$ 的项就会消失，从而变为下图所示的无力反馈的非线性解耦阻抗控制：
$\tau=\hat{A}(q)J^{-1}[\ddot{X}^d+\Lambda^{-1}[B(\dot{X}^d-\dot{X})+K(X^d-X)]-\dot{J}\dot{q}]+\hat{H}(q,\dot{q})$ 文章来源地址https://www.toymoban.com/news/detail-766848.html