机器人控制算法——移动机器人横向控制最优控制LQR算法-Toy模板网

这篇具有很好参考价值的文章主要介绍了机器人控制算法——移动机器人横向控制最优控制LQR算法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

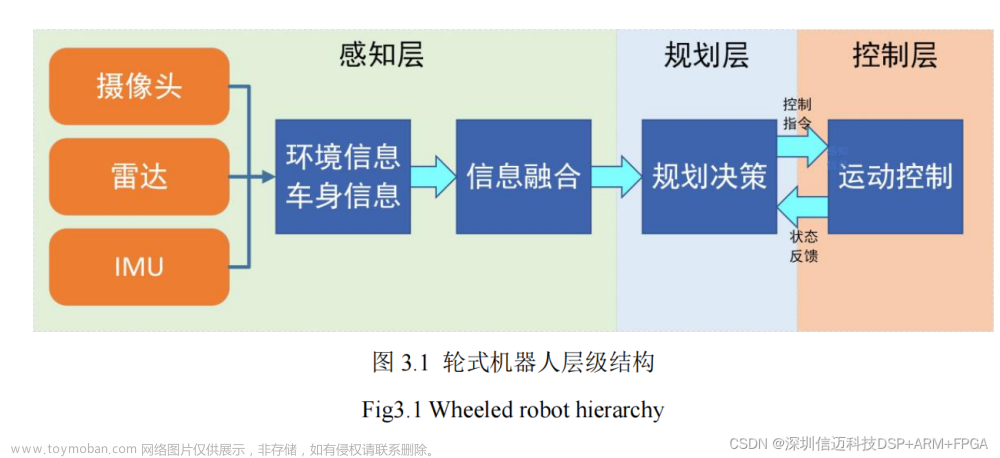
1.Introduction
LQR (外文名linear quadratic regulator)即线性二次型调节器，LQR可得到状态线性反馈的最优控制规律，易于构成闭环最优控制。LQR最优控制利用廉价成本可以使原系统达到较好的性能指标(事实也可以对不稳定的系统进行整定) ，而且方法简单便于实现，同时利用 Matlab 强大的功能体系容易对系统实现仿真。
之前已经在自动驾驶汽车上工程落地，参见自动驾驶——最优控制算法(LQR）工程化总结。
与上次不同的是，此次被控对象是移动机器人，两轮差速模型，差速模型原理参见另一篇机器人控制算法——两轮差速驱动运动模型
2. Implment LQR Algorithm for Differential Drive Motion

车辆运动学模型是根据车辆的几何关系建立的，不考虑影响车辆运动的力。以车辆后轴中点作为研究对象，在惯性坐标系OXY下，车辆运动状态可用车辆坐标(x,y)和车身航向角。v为车辆纵向行驶速度，如下图所示。
差速轮lqr,自动驾驶算法,机器人,算法,自动驾驶
则车辆运动学模型为：

其中，u1和u2分别是车辆的纵向和横向控制输入。
设车辆行驶的目标点位姿为
，则在车辆目标点处建立局部相对坐标系，如图2所示的坐标系变换示意图，则车辆当前位置相对目标位置的横纵向偏差和航向角偏差满足下列几何关系：
差速轮lqr,自动驾驶算法,机器人,算法,自动驾驶
其中，
分别为车辆的纵向偏差、横向偏差和航向角偏差。
根据公式(1)和公式(2)可得车辆在相对坐标系下的运动学模型为：

公式（3）中包含了纵向控制u1（v）和横向控制u2（w），但是本文我们只考虑横向控制。我们需要把横向控制和纵向控制解耦合。
根据(3)可得解耦后的车辆横向运动学模型为：
差速轮lqr,自动驾驶算法,机器人,算法,自动驾驶
我们需要进一步将公式16进行线性化处理，利用高等数学极限知识，当x->0,sin(x)~x,故有：

至此我们得到了机器人两轮差速动力学模型。

3. LQR Implement
在本部分，我们将使用LQR控制算法计算最优控制规律。

对矩阵A和B离散化处理

B_D = T * B
A_D = (I+0.5AT)(I-0.5A*T)^(-1)

 matrix_A_D    = (matrix_I - 0.5 * ts * matrix_A)^(-1) * (matrix_I + 0.5 * ts * matrix_A);
 matrix_B_D    = matrix_B * ts;

2.设定Q和R矩阵，Q应是2X2矩阵，R应是1X1维。
3.Riccati 方程求解：
差速轮lqr,自动驾驶算法,机器人,算法,自动驾驶

My Related Works
2. 自动驾驶-LQR工程实现（调研）
3. 自动驾驶-动力学模型-状态空间法A矩阵----c语言实现【附Github源码链接】
4. 自动驾驶——最优控制算法(LQR）工程化总结

Reference
1.基于车辆运动学模型的路径跟踪仿真及程序

如果觉得写得还不错，可以关注一下我的微信公众号，最新动态会分享在此。
差速轮lqr,自动驾驶算法,机器人,算法,自动驾驶文章来源地址https://www.toymoban.com/news/detail-766980.html

到了这里，关于机器人控制算法——移动机器人横向控制最优控制LQR算法的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

机器人控制算法——移动机器人横向控制最优控制LQR算法

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

微信扫一扫打赏

支付宝扫一扫领取红包，优惠每天领

二维码1

二维码2