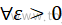大数定律&中心极限定理

1.切比雪夫不等式

切比雪夫不等式可以对随机变量偏离期望值的概率做出估计，这是大数定律的推理基础。以下介绍一个对切比雪夫不等式的直观证明。

1.1 示性函数

对于随机事件A，我们引入一个示性函数$I_A=\{\begin{array}{ll}1& ,\text{A发生}\\ 0& ,\text{A不发生}\end{array}$，即一次实验中，若$A$发生了，则$I$的值为1，否则为0。

现在思考一个问题：这个函数的自变量是什么？

我们知道，随机事件在做一次试验后有一个确定的观察结果，称这个观察结果为样本点$\omega$，所有可能的样本点的集合称为样本空间$\Omega =\left { \omega \right } $，称$\Omega$的一个子集$A$为随机事件。

例如，掷一个六面骰子，记得到数字$k$的样本点为${\omega }_k$，则 Ω = { ω 1 , ω 2 , ω 3 , ω 4 , ω 5 , ω 6 } \Omega = \{\omega_1,\omega_2,\omega_3,\omega_4,\omega_5,\omega_6\} Ω={ω1​,ω2​,ω3​,ω4​,ω5​,ω6​}，随机事件“得到的数字为偶数”为 A = { ω 2 , ω 4 , ω 6 } A = \{\omega_2,\omega_4,\omega_6\} A={ω2​,ω4​,ω6​}。

由此可知，示性函数是关于样本点的函数，即
$$I_A(\omega )=\{\begin{array}{ll}1& ,\omega \in A\\ 0& ,\omega \notin A\end{array}\text{(试验后)}$$

在试验之前，我们能获得哪个样本点也是未知的，因此样本点也是个随机事件，记为$\xi$，相应的示性函数可以记为
$$I_A=\{\begin{array}{ll}1& ,\xi \in A\\ 0& ,\xi \notin A\end{array}\text{(试验前)}$$

在试验之前，$I$的值也是未知的，因此$I$是个二值随机变量。这样，我们就建立了随机事件$A$和随机变量$I$之间的一一对应关系。

对$I$求数学期望可得
$$\mathbb{E}{I}_A=1\times P(\xi \in A)+0\times P(\xi \notin A)=P(\xi \in A)$$

$P(\xi \in A)$是什么？是样本点落在$A$里面的概率，也就是$A$事件发生的概率$P(A)$，由此我们就得到了示性函数很重要的性质：其期望值正是对应的随机事件的概率，即
$$\mathbb{E}{I}_A=P(A)$$

1.2 马尔科夫不等式

对于非负的随机变量$X$和定值$a$，考虑随机事件 A = { X ≥ a } A=\{X \ge a\} A={X≥a}，我们可以画出示性函数$I_A$关于观察值$x$的图像，如图所示：

容易发现$I_{X\ge a}(x)\le \frac{x}{a}$恒成立。把$x$换为随机变量$X$，再对该式取数学期望得
$$\mathbb{E}{I}_{X\ge a}=P(X\ge a)\le \frac{\mathbb{E}X}{a}$$
称该不等式为马尔科夫Markov不等式，

从理解上说，如果非负随机变量$X$的期望存在，则$X$超过某个定值$a$的概率不超过$\frac{\mathbb{E}}{a}$。举个简单的例子：如果我们知道所有人收入的平均数$a$，那么随机抽一个人收入超过$10a$的概率不超过$10\%$。

根据图中两个函数的差距，我们大致能理解这个不等式对概率的估计时比较粗超的。

1.3 切比雪夫不等式

对于随机变量$X$，记$\mu =\mathbb{E}X$，考虑随机事件 A = { ∣ X − μ ∣ ≥ a } A=\{|X-\mu|\ge a\} A={∣X−μ∣≥a}，其示性函数的图像如图所示：

易知$I_{|X-\mu |\ge a}\le \frac{{(x-\mu )}^2}{a^2}$恒成立。将该式$x$换成$X$并取数学期望得
$$\mathbb{E}{I}_{|X-\mu |\ge a}=P(|X-\mu |\ge a)\le \frac{\mathbb{D}X}{a^2}$$
称上面这个不等式为切比雪夫Chebyshev不等式。

从理解上来说，如果随机变量$X$的期望和方差存在，则$X$和期望值的距离大于$a$的概率不超过$\frac{\mathbb{D}X}{a^2}$，给定的范围越大（$a$越大），或$X$的方差越小，则偏离的概率越小，这和直觉是相符的。

同样的，切比雪夫不等式对概率的估计也比较粗糙。

2. 大数定律

对于一系列随机变量 { X n } \{X_n\} {Xn​}，设每个随机变量都有期望。由于随机变量之和${\sum }_{i=1}^n{X}_i$很有可能发散到无穷大，我们转而考虑随机变量的均值${\bar{X}}_n=\frac{1}{n}{\sum }_{i=1}^n{X}_i$和其期望$\mathbb{E}({\bar{X}}_n)$之间的距离。若 { X n } \{X_n\} {Xn​}满足一定条件，当$n$足够大时，这个距离会以非常大的概率接近0，这就是大数定律的主要思想。

定义：
任取$\epsilon >0$，若恒有 lim ⁡ n → ∞ P ( ∣ X ˉ n − E X ˉ n ∣ < ε ) = 1 \lim_{n \to \infty} P(\left | \bar{X}_n-\mathbb{E}\bar{X}_n \right | < \varepsilon )=1 limn→∞​P( ​Xˉn​−EXˉn​ ​<ε)=1，称 { X n } \{X_n\} {Xn​}服从（弱）大数定律，称${\bar{X}}_n$依概率收敛于$\mathbb{E}({\bar{X}}_n)$，记作
$${\bar{X}}_n\stackrel{P}{⟶}\mathbb{E}({\bar{X}}_n)$$

2.1 马尔可夫大数定律

任取$\epsilon >0$，由切比雪夫不等式可知
P ( ∣ X ˉ n − E X ˉ n ∣ < ε ) ≥ 1 − D ( X ˉ n ) ε 2 P(\left | \bar{X}_n-\mathbb{E}\bar{X}_n \right | < \varepsilon )\ge 1-\frac{\mathbb{D}({\bar{X}_n})}{{\varepsilon}^2} P( ​Xˉn​−EXˉn​ ​<ε)≥1−ε2D(Xˉn​)​
$$=1-\frac{1}{{\epsilon }^2{n}^2}\mathbb{D}(\sum _{i=1}^n{X}_i)$$
由此得到马尔可夫大数定律:
如果${\lim }_{n\to \infty }\frac{1}{n^2}\mathbb{D}({\sum }_{i=1}^n{X}_i)=0$，则 { X n } \{X_n\} {Xn​}服从大数定律。

2.2 切比雪夫大数定律

在马尔可夫大数定律的基础上，如果 { X n } \{X_n\} {Xn​}两两不相关，则方差可以拆开：
$$\frac{1}{n^2}\mathbb{D}(\sum _{i=1}^n{X}_i)=\frac{1}{n^2}\sum _{i=1}^n\mathbb{D}{X}_i$$
如果$\mathbb{D}{X}_i$有共同的上界c，则
$$\frac{1}{n^2}\mathbb{D}(\sum _{i=1}^n{X}_i)\le \frac{nc}{n^2}=\frac{c}{n}$$
P ( ∣ X ˉ n − E X ˉ n ∣ < ε ) ≥ 1 − c ε 2 n P(\left | \bar{X}_n-\mathbb{E}\bar{X}_n \right | < \varepsilon )\ge 1-\frac{c}{{\varepsilon}^2n} P( ​Xˉn​−EXˉn​ ​<ε)≥1−ε2nc​
由此得到切比雪夫大数定律：
如果 { X n } \{X_n\} {Xn​}两两不相关，且方差有共同的上界，则 { X n } \{X_n\} {Xn​}两两不相关服从大数定律。

3. 中心极限定理

大数定律研究的是一系列随机变量 { X n } \{X_n\} {Xn​}的均值${\bar{X}}_n=\frac{1}{n}{\sum }_{i=1}^n{X}_i$是否会依概率收敛于其期望$\mathbb{E}({\bar{X}}_n)$这个数值，而中心极限定理进一步研究${\bar{X}}_n$服从什么分布。若 { X n } \{X_n\} {Xn​}满足一定的条件，当$n$足够大时，${\bar{X}}_n$服从正态分布，这就是中心极限定理的主要思想，这也体现了正态分布的重要性和普遍性。

3.1 独立同分布中心极限定理（林德贝格-勒维）

如果 { X n } \{X_n\} {Xn​}独立同分布，且$\mathbb{E}X=\mu$，$\mathbb{D}X={\sigma }^2>0$，则$n$足够大时${\bar{X}}_n$近似服从正态分布$N(\mu ,\frac{{\sigma }^2}{n})$，即
$$\underset{x\to \infty }{\lim }P(\frac{{\bar{X}}_n-\mu }{\sigma /\sqrt{n}}<a)=\Phi (a)={\int }_{-\infty }^a\frac{1}{\sqrt{2\pi }}{e}^{-t^2/2}dt$$文章来源地址https://www.toymoban.com/news/detail-767243.html

到了这里，关于大数定律&中心极限定理的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！