【数据结构】迷宫问题实现(包含界面)-Toy模板网

这篇具有很好参考价值的文章主要介绍了【数据结构】迷宫问题实现(包含界面)。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

🎈🎈

问题描述：假设迷宫由m行n列构成，有一个入口和一个出口，入口坐标为(1,1),出口坐标为(m,n),试设计并验证一下算法：找出一条入口通往出口的路径，或报告一个"无法通过"的信息。

具体需求如下：

用C语言实现顺序存储结构上队列的基本操作，然后利用该队列的基本操作找出迷宫的一条最短路径。

设计一个二维数组MAZE[m+2][n+2]表示迷宫，数组元素为0表示该位置可以通过，数组元素为1表示该位置不可以通行。MAZE[1][1],MAZE[m][n]分别表示为迷宫的出口和入口。

输入迷宫的大小m行和n列，动态生成二维数组；由随机数产生0或1

迷宫的任意位置上均有八个可以移动的方向。

若存在走出迷宫的路径，则动态展示走出迷宫的过程。

✨✨

先给大家看看最终的运行效果：

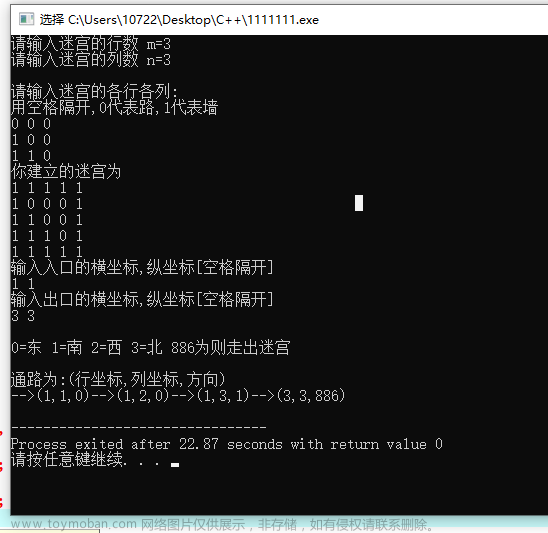
①.未找到路径的情况

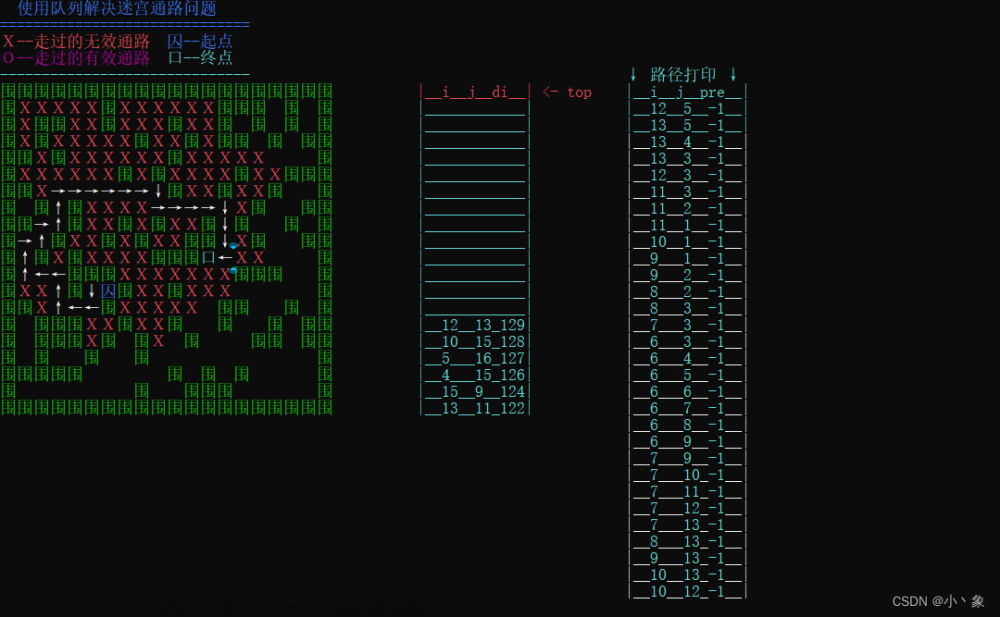
②.找到最短路径，并动态演示从起点走到终点的过程

OK，我愿称之为史上最变态迷宫问题——不仅有八个移动方向，还要设计界面，动态展示走出迷宫的过程。话不多说，我们现在来一步步实现迷宫算法吧！

注：此迷宫用c语言实现，界面用的是c++。当然了，我们主要是理解迷宫的实现算法(也就是c语言写的代码)，图形界面可以随便选c、c++或者别的高级语言实现。

算法实现步骤：

实现顺序存储结构上队列的基本操作

这个我就不详细说明了，直接给老铁们上源码链接：

顺序队列的实现

动态创建迷宫

创建迷宫我们分两步：

①.动态创建二维数组并初始化为0

这里我们使用malloc函数即可实现数组的动态创建，代码如下：

int** CreateArray(int m, int n) {
    int i, j;
    int** array;
    array = (int**)malloc((m)*sizeof(int*));
    for(i=0; i<m; i++) {
        array[i] = (int*)malloc(sizeof(int)*(n));
    }
    for(i=0; i<m; i++) {
        for(j=0; j<n; j++) {
            array[i][j] = 0;//初始化为0
        }
    }
    return array;
}

注：

(1) 建立迷宫，注意m*n的迷宫需要进行扩展，即实际迷宫大小为(m+2)*(n+2)，扩展部分的元素设置为1。这是因为C语言不会进行数组越界检查，为了防止我们在找路径时会跑到迷宫之外的存储位置上，要给迷宫“围上一堵墙”。

(2)CreatyArray函数并未体现创建了(m+2)*(n+2)的数组，这是因为我给次函数传递的实参为(m+2,n+2)。即实际调用时为“CreatyArray(m+2, n+2);”

②.随机给数组元素赋1——0表示可行，1表示不可行

随机赋值也比较简单，使用随机函数srand()即可

代码如下：

int** MakeMaze(int m, int n) {
    int i, j;
    int** maze;
    srand(time(0));
    maze = CreateArray(m+2, n+2);
    for(i = 0; i<n+2; i++) {
        maze[0][i] = 1;
        maze[m+1][i] = 1;
    }
    for(i = 0; i<m+2; i++) {
        maze[i][0] = 1;
        maze[i][n+1] = 1;
    }
    for(i=1; i<m+1; i++) {
        for(j=1; j<n+1; j++) {
            maze[i][j] = rand()%2%2;
        }
    }
    maze[1][1] = maze[m][n] = 0;
    return maze;
}

注：

(1)连续两次%2可以使元素为0概率变大，即该迷宫存在路径的可能性更大。（哈哈，我们老师说的，我没去深究）

(2)迷宫入口maze[1][1]和迷宫出口maze[m][n]必须可行，即值为0

判断是否存在走出迷宫的路径

这个算法实际上是找出走出迷宫的所有可能路径，用到了顺序队列。

算法思想：

首先将入口入队，以入口为起点判断其八个方向的点是否可行，如果可行就将该点入队。

当队列不空并且未到达终点时，继续对队列的队头元素判断其八个方向的点是否可行，如果可行就将该点入队。

每判断完队列中的一个队头元素，就将该队头元素出队，并获取下一个队头元素。这里的出队其实是逻辑上的出队，是队列的头指针指向了下一个元素。

因此，其实我们一直都是对队列的队头元素判断其八个方向，并重复对队列进行入队出队操作。

注：

我们最好边画图边看代码，有助于理解寻找路径的过程。

代码如下：

Status IfHaveWay(int** maze, int m, int n, SqQueue* Q) {
    int i, success = 0, m2, n2, count = 0;
    QElemType head = {1,1,-1, 0}, e;
    int** flag = CreateArray(m+2, n+2);//标志数组
    int direction[8][2] = {{-1,0},{-1,1},{0,1},{1,1},{1,0},{1,-1},{0,-1},{-1,-1}};//存放八个方向的位置偏移量
    flag[1][1] = 1;
    EnQueue(Q, head);
    while(!success && !QueueEmpty(*Q)) {
        for(i=0; i<8; i++) {
            m2 = head.row+direction[i][0];//迷宫的行
            n2 = head.column+direction[i][1];//迷宫的列
            if(maze[m2][n2] == 0 && flag[m2][n2] == 0) { //该点未被走过
                e.row = m2;
                e.column =n2;
                e.pre = head.pos;
                e.pos = QueueLength(*Q)+count;
                EnQueue(Q, e);
                flag[m2][n2] = 1;
            }
            if(e.row == m && e.column == n) {
                success = 1;//找到出口，退出循环
                break;
            }

        }
        DeQueue(Q, &e);
        GetHead(*Q, &head);
        count++;
    }
    if(!success)
        return FALSE;
    else
        return TRUE;
}

若存在路径，则找出最短路径

在上一步的判断路径是否存在过程中我们已经得到了一个顺序队列，里面是走出迷宫的全部可能路径。

那么如何从这些路径中找出最短路径呢？方法很简单：

初始化栈S

从得到的顺序队列队尾元素开始，依次找元素的前驱，并存入栈中，直至起点(1,1)，这样可以找到最短路径。

又因为栈是“先进后出”的，所以从栈顶至栈底即为走出迷宫的路径。

注：

最好画图理解，光看文字和代码十分抽象。

代码如下：

SqStack FindWay(SqQueue Q) {
    SqStack S;
    InitStack(&S);
    SElemType tmp;
    int p = Q.rear-1, pre = Q.base[p].pre;
    tmp.column = Q.base[p].column;
    tmp.pos = Q.base[p].pos;
    tmp.pre =  Q.base[p].pre;
    tmp.row = Q.base[p].row;
    Push(&S, tmp);
    p--;
    while(p>=0) {
        if(pre == Q.base[p].pos) {
            tmp.column = Q.base[p].column;
            tmp.pos = Q.base[p].pos;
            tmp.pre =  Q.base[p].pre;
            tmp.row = Q.base[p].row;
            Push(&S, tmp);
            pre = Q.base[p].pre;
        }
        p--;

    }
    return S;

}

实现迷宫的图形化界面设计

代码如下：

#include "widget.h"
#include<maze.h>
#include "ui_widget.h"
#include <QColor>
#include <QTimer>
#include <QMessageBox>
Widget::Widget(QWidget *parent) :
    QWidget(parent),
    ui(new Ui::Widget){

    ui->setupUi(this);
    this->people.load(":/Image/people.png");
    this->sign.load(":/Image/flag.png");
    this->wall.load(":/Image/wall.png");
}

Widget::~Widget()
{

    delete ui;
}
void Widget::paintEvent(QPaintEvent *event)
{
    if(m!=0 && n!= 0){
        QPainter painter(this);// 实例化画家对象，this指定的是绘图设备
        for(int i=0;i<=m+2;i++){
            painter.drawLine(i*60+25,25,i*60+25,(m+2)*60+25);// 画竖线
        }
        for(int i=0;i<=n+2;i++){
               painter.drawLine(25,i*60+25,(n+2)*60+25,i*60+25);//画横线
          }

        // 设置画笔
        QPen pen(QColor(255,0,0));
        // 设置画笔宽度
        pen.setWidth(2);
        pen.setStyle(Qt::SolidLine);//设置画笔样式
        painter.setRenderHint(QPainter::Antialiasing);//抗锯齿
        painter.setPen(pen);
        for(int i=0;i<m+2;i++)
        {
            for(int j=0;j<n+2;j++)
            {
                if(maze[i][j]==1)
                {
                     painter.drawPixmap(i*60+30,(j)*60+28,this->wall);

                }
            }
        }
        painter.drawPixmap(posX,posY,this->people);//画运动的人
        painter.drawPixmap(m*60+45,(n)*60+40,this->sign);//画终点的图标
    }
}

void Widget::on_checkBt_clicked()//确定按钮点击事件
{
    SqStack SWay;
    SqQueue Q;
    SElemType tmp;
    InitStack(&SWay);
    m = ui->maze_m->text().toInt();
    n = ui->maze_n->text().toInt();
    QMessageBox *mbox = new QMessageBox();
    mbox->setIcon(QMessageBox::Information);
    if(n != 0 && m != 0){
        this->maze = MakeMaze(m, n);
        InitQueue(&Q);
        if(!IfHaveWay(maze, m,n, &Q)) {
            mbox->setText("未找到走出迷宫的路径");
            mbox->show();
            update();
        }else{//找到路径
            QTimer *timer = new QTimer(this);//设置定时器
            timer->start(1000);
            SWay = FindWay(Q);

            connect(timer,&QTimer::timeout,[=](){
                if(StackEmpty(SWay)){//栈为空，说明路径已走完
                    timer->stop();
                    mbox->setText("成功走出迷宫,Congratulations!");
                    mbox->show();
                    posX = 90, posY = 90;
                    update();
                    return;
                }
                Pop((SqStack*)(&SWay), (SElemType*)(&tmp));//将存放路径的栈的元素依次弹出
                posX = tmp.row*60+30, this->posY = tmp.column*60+30;
                update();
            });
        }
    }else{
        mbox->setText("请输入有效的长和宽");
        mbox->show();
    }
}

最后给大家贴个我实现迷宫用到的文件截图：