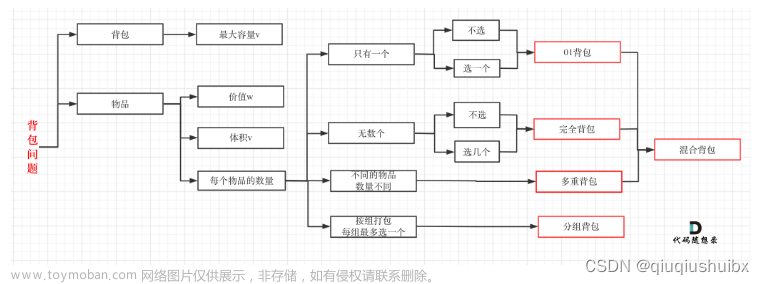
问题描述:
容量为C的背包选择装物品,有n个物品,它们有各自的体积wi和价值vi,如何让背包里装入的物品具有最大价值?
解题思路:
也就是n个物品选择装入背包,每个物品都有两种选择,是(1)或否(0),
建模: xi表示当前第i个物品是否选择,xi取值为(0,1)。
约束条件:,选择的物品重量小于等于C,且这几样物品加起来的价值最大。
动态规划:
动态规划算法通常用于求解具有某种最优性质的问题。动态规划算法与分治法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。如果我们能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,这样就可以避免大量的重复计算。我们可以用一个表来记录所有已解的子问题的答案,只要它被计算过,就将其结果填入表中。这就是动态规划法的基本思路
适用动态规划的问题必须满足最优化原理和无后效性 。 最优化原理(最优子结构性质)
最优化原理可这样阐述:一个最优化策略具有这样的性质,不论过去状态和决策如何,对前面的决策所形成的状态而言,余下的诸决策必须构成最优策略。简而言之,一个最优化策略的子策略总是最优的。一个问题满足最优化原理又称其具有最优子结构性质。
无后效性 将各阶段按照一定的次序排列好之后,对于某个给定的阶段状态,它以前各阶段的状态无法直接影响它未来的决策,而只能通过当前的这个状态。换句话说,每个状态都是过去历史的一个完整总结。这就是无后向性,又称为无后效性。
动态规划没有统一的处理方法,必须根据问题的各种性质并结合一定的技巧来处理,一般最常见的就是用公式求出每个位置的最大值,然后用二维列表保存,这是最基础的,之后再想办法优化。
递推关系:
1、V(i,j):当前背包容量 j,前 i 个物品最佳组合对应的最大价值
首先对当前第i个物品是否选择装,背包容量装不下当前物品,所以选择不装,所以当前最大价值就是前i-1个物品时的最大价值。V(i-1,j)
2如果背包容量可以装下当前的物品,就需要判断是否装。
max(不装v(i-1,j), ),也就是不装时最大价值等于前i-1个物品时的最大价值,装就是最大价值等于装下的这个物品的价值加上背包容量为(j-wi)(减去当前这个物品的wi)时能装前i-1个物品时的最大价值(vij-wi),选取两者的最大值。
举例:4个物品:

通过填表的方式:
追踪解:
如果当前i个物品的最大价值和前i-1个东西的最大价值一样时,说明第i个物品没放,则x;=0。反之当前i个物品的最大价值大于前i-1个物品的最大价值时,说明放了第i个物品,则x;=1。
代码:(Python):
def bag(n, c, w, v):
res = [[0 for j in range(c + 1)] for i in range(n + 1)]#初始值全赋值为0
for i in range(1, n + 1):
for j in range(1, c + 1):
res[i][j] = res[i - 1][j]#根据公式填写表,得到最大收益
if j >= w[i - 1] and res[i][j] < res[i - 1][j - w[i - 1]] + v[i - 1]:
res[i][j] = res[i - 1][j - w[i - 1]] + v[i - 1]
return res
def show(n, c, w, res):
print('最大收益为:', res[n][c])
x = [False for i in range(n)]
j = c
for i in range(1, n + 1): # (1,6)
if res[i][j] > res[i - 1][j]:#判断项目是否投资
x[i - 1] = True
j -= w[i - 1] #投资后(资金-当前金额投资)
print('选择的项目为:')
for i in range(n):
if x[i]:
print('第', i + 1, '个,', end='') #展示结果
print('')
#实例
n = 5
c = 10
w = [2, 2, 6, 5, 4]
v = [6, 3, 5, 4, 6]
res = bag(n, c, w, v)
show(n, c, w, res)利用动态规划解决此问题的效率即是填写此张表的效率,所以动态规划的 时间效率为O(number*capacity)=O(n*c),
由于用到二维数组存储子问题的解,所以动态规划的 空间效率为O(n*c);
文章来源地址https://www.toymoban.com/news/detail-767371.html
优化,从上述的填表的过程中,我们可以发现vij的值只与上一行有关。
可以将V缩减成一维数组,从而达到优化空间的目的,状态转移方程转换为 B(j)= max{B(j), B(j-w(i))+v(i)}; 每一次推导V(i)(j)是通过V(i-1)(j-w(i))来推导的,所以要保留上一行前面的值。所以一维数组中j的扫描顺序应该从大到小(capacity到0),否者前一次循环保存下来的值将会被修改,从而造成错误。文章来源:https://www.toymoban.com/news/detail-767371.html
到了这里,关于01背包问题----动态规划 -----python代码、优化的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!