动态规划(DP)---背包二维图-Toy模板网

这篇具有很好参考价值的文章主要介绍了动态规划(DP)---背包二维图。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

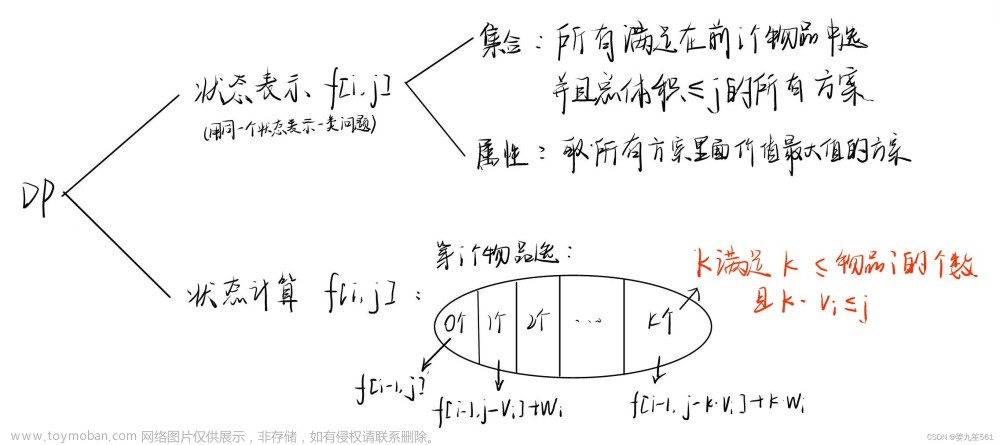
状态方程：dp[i][j] = max(dp[i - 1][j],dp[i - 1][j - w[i]] + v[i])

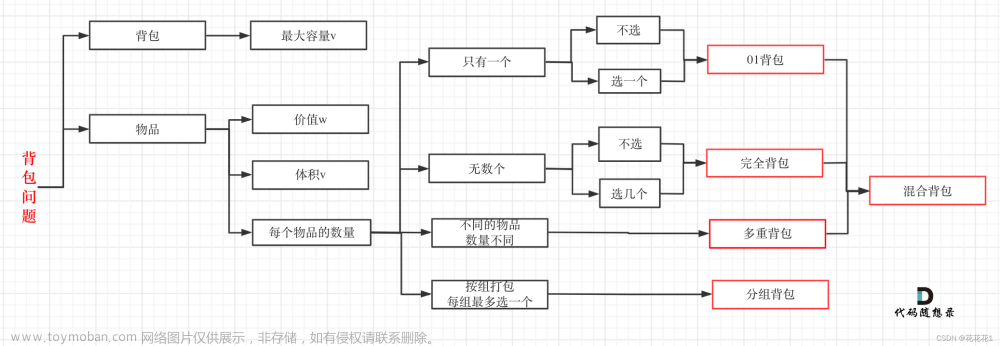
应该是看完我写的DP文章来的吧，如果没有看到，希望看看DP那个文章结合这个理解，DP那个文章内部写了我对于01背包类型的想法与思路，有时间的网友可以了解hhh。

分析这个东东的时候，其实是四个方向嘛，我推荐要是理解这个东西，从第一个物品开始枚举，从背包正好没有空间开始。

我就假设一下吧，背包容量为8

体积价值

第一个 2 3

第二个 3 4

第三个 4 5

第四个 5 6

分析状态方程，我比较喜欢给他拆成独立的个体，也就是每行为一个整体，开始分析第一个物品，第一个物品放入的开始应该是 j = 2，这个时候背包正好装满，然后到j = 3，这时的背包剩出一个空间，然后j = 4 以此类推到最后j = 8，这个第一行存储的是最开始咱们枚举第一个物品且只能放一个的最大金额；然后枚举第二个物品，在这种情况，我们要注意这里比较的时候跟上面比较不一样，上面是与0比较金额，而这里咱们从j = 3开始，这个时候应该塞进第二个物品，因为这个时候会跟第一个比较因为4 > 3所以要二而不要一，然后j = 4,这个时候会跟第一个比较以此类推.....

dp[1][2] = max(dp[0][2],dp[0][0] + 3)

dp[1][3] = max(dp[0][3],dp[0][1] + 3)

dp[1][4] = max(dp[0][4],dp[0][2] + 3)

dp[1][5] = max(dp[0][5],dp[0][3] + 3)........

---------------------------------------------------

dp[2][3] = max(dp[1][2],dp[1][0] + 4)

dp[2][4] = max(dp[1][4],dp[1][1] + 4)

dp[2][5] = max(dp[1][5],dp[1][2] + 4)

dp[2][6] = max(dp[1][6],dp[1][3] + 4)........

---------------------------------------------------

.......

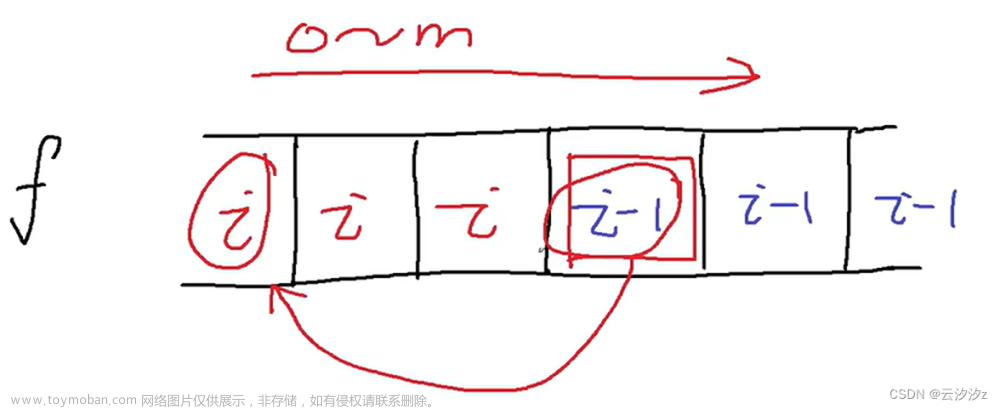
如果网友画出了二维图，我们可以发现每一次的比较都是这个位置上面的值与左上角的左面前的第几个数进行比较。

那我们在脑海中想象一下，这样的过程是不是在上一位没有加当前枚举到的数的最大金额与前面减掉正好可以容纳当前枚举到的数所占有的空间（这个时候的值就是上一层通过递推得来的最大金额，类似记忆化吧）进行比较。以此类推是不是就是看你加上这个物品与释放出能够容纳这个物品空间来加上这个物品的价值来比较，哪个大哪个就是最大金额。有点绕，但是反复琢磨一下吧，这个不是一时半会可以解决的，但是切记不要忘记dp数组的含义，否则到最后不仅浪费时间而且一但思路走进误区还要花费更多时间去纠正。

注意一下，这里咱们要是滚动数组，变成一维数组的话，这里的遍历就应该反向遍历了，因为只有反向遍历才不会覆盖值，从而导致比较时出现错误。

好了，今天的分享到此结束啦，希望你可以理解他啦，要是有不懂的地方可以在评论区留言，本文作者仅是大一新生，也就是对这个内容自己的胡说八道哈哈哈，感谢观看，希望大佬纠正。文章来源地址https://www.toymoban.com/news/detail-767822.html

到了这里，关于动态规划(DP)---背包二维图的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！