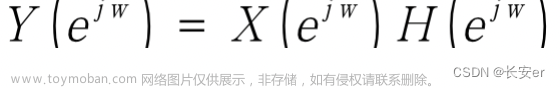现代信号处理实验：MATLAB实现LD算法进行AR估计-Toy模板网

这篇具有很好参考价值的文章主要介绍了现代信号处理实验：MATLAB实现LD算法进行AR估计。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

MATLAB实现LD算法进行AR估计

利用给定的一组样本数据估计一个平稳随机信号的功率谱密度称为功率谱估计，又称谱估计。谱估计的方法可以分成经典谱估计和现代谱估计。

经典谱估计又称为非参数化的谱估计，分为直接法和间接法。直接法是指直接计算样本数据的傅里叶变换，即获取频谱，然后计算频谱和其共轭的乘积，就得到功率谱；间接法是指先计算样本数据的自相关函数，然后计算自相关函数的傅里叶变换，即得到功率谱。经典谱估计存在很多的缺陷，主要原因是对数据加窗时默认在窗外未观测到的数据的自相关系数为 0，这显然是不切实际的；此外样本数据是有限长的，而经典谱估计往往需要较长的数据才能获得较好性能，而且加窗函数也容易造成谱的模糊，因此我们需要参数化的谱估计，也就是现代谱估计。

现代谱估计中一类常用的模型是AR模型估计。

AR估计原理

AR 模型的表达式为：
ld算法 matlab,通信专业课程笔记,信号处理,matlab

上式两边同时作 Z 变换，得到：
ld算法 matlab,通信专业课程笔记,信号处理,matlab

AR 模型的原理就是根据观测到的数据x(n)来估计 ${a_i}$ ，从而估计输入信号的功率谱。具体来说就是将输入信号x(n)看成一个均值为 0，方差为 $\sigma^2$ 的高斯噪声通过信道得到的；先通过观测数据估计信道参数 ${a_i}$ ，再结合 z 变换公式来计算输入信号的功率谱。

AR 过程的线性预测和 Levinson-Durbin 算法
ld算法 matlab,通信专业课程笔记,信号处理,matlab

求解上述Yule-Walker方程的常用算法是 Levinson-Durbin 算法，具体推导过程如下：p-1 阶的 Yule-Walker 方程如下：

ld算法 matlab,通信专业课程笔记,信号处理,matlab

代码实现

算法步骤：

根据 Levinson-Durbin 算法进行递推，来计算 AR 模型的各阶参数。采用最终预测误差 FPE 法来确定 AR 模型阶数 p。

初始化：
迭代计算：
若k>p或者误差小于阈值，返回各阶次参数
对比估计信号和实际信号，观察并分析结果

代码：

LD_AR function函数存放在LD_AR.m文件中：

function [R,order, params, var] = LD_AR(x)
N = length(x)-1;

%% 自相关矩阵
R = zeros(N, 1);
for n = 1:N
   R(n) = x(1:N-n+1) * (x(n:N))' /N;
end

%% LD 算法
a = zeros(N+1,N+1);
rho = zeros(1,N+1);
FPE = zeros(1,N+1);
rho(1) = R(1);
a(1,1) = -R(2)/R(1);
rho(2) = rho(1)*(1-abs(a(1,1))^2);
FPE(1) = (N+1)/(N-1) * rho(2);
for k=2:N-1
    S = 0;
    for m = 1:k-1
        S = S + a(k-1,m) * R(k-m+1);
    end
    a(k,k) = -(R(k+1)+S)/rho(k);
    for i = 1:k-1
        a(k,i) = a(k-1,i) + a(k,k) * a(k-1,k-i);
    end
    rho(k+1) = rho(k)*(1-a(k,k)^2);
    FPE(k) = (N+k)/(N-k) * rho(k+1);
end

%% 利用FPE确定AR模型阶数
min = FPE(1);
disp 'min:'
disp(min)
for k = 2:N-1
    if abs(FPE(k))<abs(min)
        min = FPE(k);
        order = k;
    end
end
params = [1, a(order,1:order)];
var = abs(rho(order+1));
end

main.m文件：文章来源地址https://www.toymoban.com/news/detail-768116.html

clear;
clc;

%% 产生一组样本点
awgn_noise = randn(1,1000); 
a_model = [1 -0.6 0.4 -0.3]; 
% a_model = [1 -0.4 0.2 -0.2 0.4]; 
x = filter(1, a_model, awgn_noise);

%% LD算法估计AR参数
[R,order, a, var] = LD_AR(x)

%% 原始信号 s
number=1000;
w = linspace(-pi,pi,number); 
s = zeros([1,number]);
for m = 1:number 
    c = w(m); 
    kk = [1: length(a_model)-1];
    s(m) = 1 /(abs(1+ a_model(2:end)* exp(-1i*c*kk')))^2; 
end  

%% 估计信号 s_hat
s_hat = zeros([1,number]);
for m = 1:number 
    c = w(m); 
    kk = [1: length(a)-1];
    s_hat(m) = 1 /(abs(1+ a(2:end)* exp(-1i*c*kk')))^2; 
end  

%% 绘制频谱
figure;
set(gcf,'position',[700, 200, 1400, 350])
subplot(1,3,1);
plot(w,s, 'b');
grid on
set(gca,'Xtick',[-pi,-pi/2,0, pi/2,pi]);
set(gca,'XTickLabel',{'-pi' '-pi/2' '0' 'pi/2' 'pi'});
title('原始信号功率谱','fontsize', 12); 
xlabel('频率','fontsize', 12);
ylabel('功率','fontsize', 12);
ylim([0,7]);

subplot(1,3,2);
plot(w,s_hat, 'r-'); 
grid on
set(gca,'Xtick',[-pi,-pi/2,0, pi/2,pi]);
set(gca,'XTickLabel',{'-pi' '-pi/2' '0' 'pi/2' 'pi'});
title('LD算法进行AR估计功率谱', 'fontsize', 12); 
xlabel('频率','fontsize', 12);
ylabel('功率','fontsize', 12);
ylim([0,7]);

subplot(1,3,3);
plot(w,s,'b'); 
hold on
plot(w,s_hat, 'r--');
hold off
grid on
set(gca,'Xtick',[-pi,-pi/2,0, pi/2,pi]);
set(gca,'XTickLabel',{'-pi' '-pi/2' '0' 'pi/2' 'pi'});
title('原始信号功率谱和LD算法进行AR估计比较', 'fontsize', 12); 
xlabel('频率','fontsize', 12);
ylabel('功率','fontsize', 12);
legend('原始信号','AR估计信号')
ylim([0,7]);


% clc;
% clear;
% 
% % 构造加入高斯白噪声的样本点函数
% f1=0.4;
% f2=0.2;
% N=input('产生的样本点个数N:');
% n=1:N;
% wn=randn(1,N);% 产生高斯白噪声
% xn=sin(2*pi*f1*n+pi/3)+10*sin(2*pi*f2*n+pi/4);
% yn=xn+wn;
% 
% Rx=xcorr(yn,'biased');
% 
% k=1:N;
% f=k/N;
% Sx=abs(fft(Rx,N));
% plot(f,Sx);
% title('功率谱');
% xlabel('f');
% ylabel('Sx');
% 
% % 根据自相关函数估计f1,f2
% sxk=zeros(1,N/2);
% for k=1:N/2
%     sxk(k)=Sx(k);
% end
% 
% [pks,locs]=findpeaks(sxk,'SortStr','descend');
% locs(1)
% locs(2)
% for i=1:2
%     fprintf('预测结果：f%d=%f\n',i,locs(i)/N);
% end