数据结构第六课 -----链式二叉树的实现-Toy模板网

这篇具有很好参考价值的文章主要介绍了数据结构第六课 -----链式二叉树的实现。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

作者前言

🎂 ✨✨✨✨✨✨🍧🍧🍧🍧🍧🍧🍧🎂
🎂 作者介绍： 🎂🎂
🎂 🎉🎉🎉🎉🎉🎉🎉 🎂
🎂作者id：老秦包你会， 🎂
简单介绍：🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂
喜欢学习C语言和python等编程语言，是一位爱分享的博主，有兴趣的小可爱可以来互讨 🎂🎂🎂🎂🎂🎂🎂🎂
🎂个人主页::小小页面🎂
🎂gitee页面:秦大大🎂
🎂🎂🎂🎂🎂🎂🎂🎂
🎂 一个爱分享的小博主欢迎小可爱们前来借鉴🎂

二叉树

前面粗略的介绍了二叉树
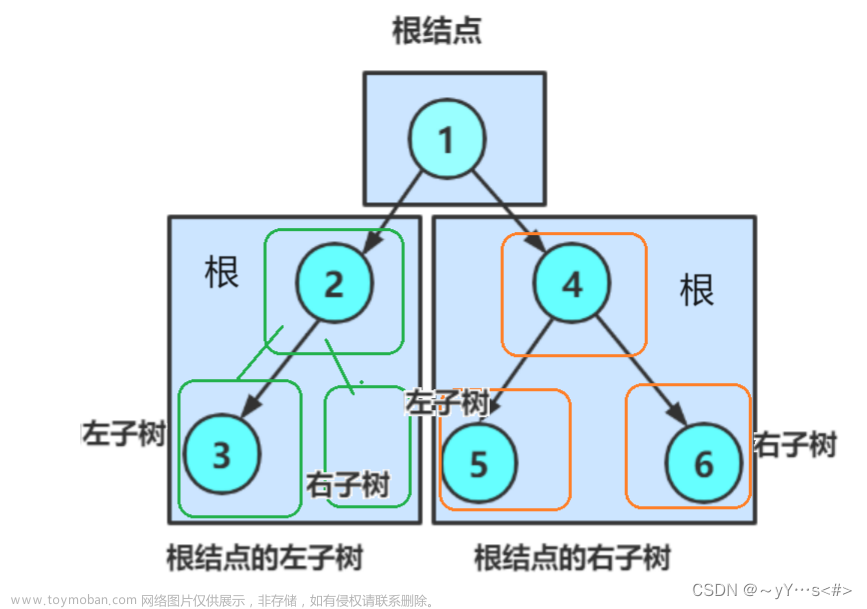
二叉树主要有两种空树和非空树
而非空树拆分为 : 根节点和左子树和右子树
数据结构第六课 -----链式二叉树的实现,数据结构
二叉树的性质

若规定根节点的层数为1，则一棵非空二叉树的第i层上最多有 2^(i-1)个结点.
若规定根节点的层数为1，则深度为h的二叉树的最大结点数是2^h -1 .
对任何一棵二叉树, 如果度为0其叶结点个数为n0 , 度为2的分支结点个数为n2 ,则有 n0＝ n2＋1
若规定根节点的层数为1，具有n个结点的满二叉树的深度，h=log(n+1) . (ps：是log以2
为底，n+1为对数)
对于具有n个结点的完全二叉树，如果按照从上至下从左至右的数组顺序对所有节点从0开始编号，则对于序号为i的结点有：
1. 若i>0，i位置节点的双亲序号：(i-1)/2；i=0，i为根节点编号，无双亲节点
2. 若2i+1<n，左孩子序号：2i+1，2i+1>=n否则无左孩子
3. 若2i+2<n，右孩子序号：2i+2，2i+2>=n否则无右孩子

二叉树的遍历

学习二叉树结构，最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。

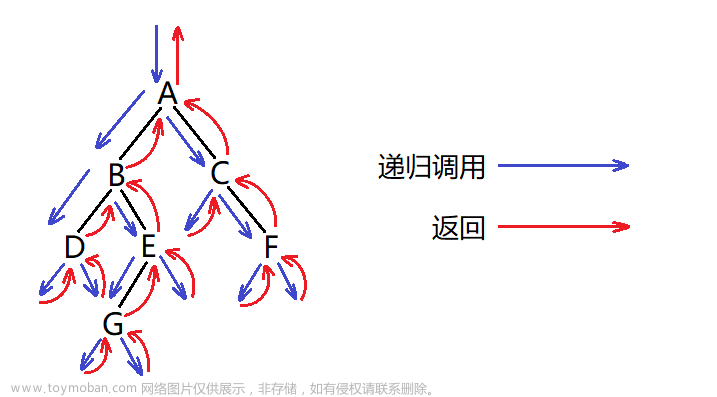
按照规则，二叉树的遍历有：前序/中序/后序的递归结构遍历：

前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。(根 ->左 ->右)
中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。(左->根->右)
后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。(左->右->根)

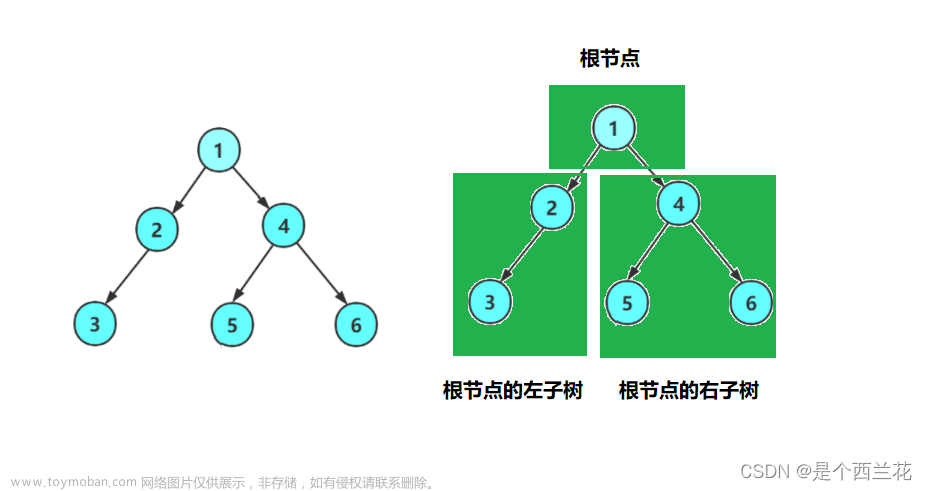
为此特意构建一个二叉树

#include<stdio.h>
#include<stdlib.h>
typedef int BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType* val;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* rigth;

}BinaryTreeNode;
BinaryTreeNode* CreateNode(BTDataType elemest)
{
	BinaryTreeNode* p = (BinaryTreeNode*)malloc(sizeof(BinaryTreeNode));
	if (p == NULL)
	{
		perror("malloc");
		return -1;
	}
	p->val = elemest;
	return p;
}
int main()
{
	BinaryTreeNode* n1 = CreateNode(1);
	BinaryTreeNode* n2 = CreateNode(2);
	BinaryTreeNode* n3 = CreateNode(3);
	BinaryTreeNode* n4 = CreateNode(4);
	BinaryTreeNode* n5 = CreateNode(5);
	BinaryTreeNode* n6 = CreateNode(6);
	n1->left = n2;
	n1->rigth = n4;
	n2->left = n3;
	n2->rigth = NULL;
	n3->left = NULL;
	n3->rigth = NULL;
	n4->left = n5;
	n4->rigth = n6;
	n5->left = NULL;
	n5->rigth = NULL;
	n6->left = NULL;
	n6->rigth = NULL;
	return 0;
}

前序遍历

我们以上面图片为例
我们可以写成：
1 2 3 N N N 4 5 N N 6 N N
代码：

void PreOrder(BinaryTreeNode* n1)
{
	if (n1 == NULL)
	{
		printf("NULL ");
		return;
	}
		

	printf("%d ", n1->val);
	PreOrder(n1->left);
	PreOrder(n1->rigth);
}

数据结构第六课 -----链式二叉树的实现,数据结构

中序遍历

我们可以写成：N 3 N 2 N 1 N 5 N 4 N 6 N
代码：

void InOrdef(BinaryTreeNode* n1)
{
	if (n1 == NULL)
	{
		printf("NULL ");
		return;
	}
	PreOrder(n1->left);
	printf("%d ", n1->val);
	PreOrder(n1->rigth);
}

后序遍历

我们可以写成： N N 3 N 2 N N 5 N N 6 4 1
代码：

void PostOrder(BinaryTreeNode* n1)
{
	if (n1 == NULL)
	{
		printf("NULL ");
		return;
	}
	PreOrder(n1->left);
	PreOrder(n1->rigth);
	printf("%d ", n1->val);
}

小例子

叶子节点个数
思路:左子树的节点个数加上右子树的节点个数加上根节点

//节点个数
int TreeSize(BinaryTreeNode* n1)
{
	if (n1 == NULL)
		return 0;
	return 1 + TreeSize(n1->left) + TreeSize(n1->rigth);
}

叶节点个数
思路:左子树的叶节点个数加上右子树的叶节点个数加上根节点需要注意的是为空树.和只有根节点的情况

//叶节点的个数
int TreeLeafSize(BinaryTreeNode* n1)
{
	//为空树
	if (n1 == NULL)
		return 0;
	//只有一个节点
	if (n1->left == NULL && n1->rigth == NULL)
		return 1;
	return TreeLeafSize(n1->left) + TreeLeafSize(n1->rigth);
}

树的高度
思路:左子树的高度和右子树高度比较,大的高度加上1就是整个二叉树的高度,需要注意的是空树情况下

int TreeHeigth(BinaryTreeNode* n1)
{
	if (n1 == NULL)
		return 0;
	if (n1->left == NULL && n1->rigth == NULL)
		return 1;
	int a = TreeHeigth(n1->left);
	int b = TreeHeigth(n1->rigth);
	return (a > b ? a : b) + 1;
}

#第k层的节点
思路: 左子树的第k-1层的节点个数加上右子树的第k-1层的节点个数,如果k为0就是空,k=1,就是1

int NodeNum(BinaryTreeNode* n1, int k)
{
	if (n1 == NULL)
		return 0;
	if (k == 0)
		return 0;
	if (k == 1)
		return 1;
	return NodeNum(n1->left, k - 1) + NodeNum(n1->rigth, k - 1);
}

层次遍历
思路:层次遍历就是从第一层开始横向遍历
我们可以借助队列的性质,先进先出,我们先开始插入根节点,然后开始进行循环判断,只要出去的节点的左右孩子不为NULL就插入到队列,直到队列为空
数据结构第六课 -----链式二叉树的实现,数据结构

// 层序遍历
void BinaryTreeLevelOrder(BinaryTreeNode* root)
{
	//创建一个队列
	Queue Qu;
	//初始化
	QueueInit(&Qu);
	//插入的是节点,
	if (root != NULL)
		QueuePush(&Qu, root);
	while (QueueSize(&Qu))
	{
		BinaryTreeNode* from = QueueFront(&Qu);
		
		
		printf("%d ", from->val);
		//删除
		QueuePop(&Qu);
		//需要注意的是删除只是释放掉存储了二叉树节点的地址的空间,并没有释放二叉树节点
		if (from->left != NULL)
		{
			QueuePush(&Qu, from->left);
		}
		if (from->rigth != NULL)
		{
			QueuePush(&Qu, from->rigth);
		}
		
	}
	printf("\n");
	QueueDestroy(&Qu);
	
	
	
}

这个是打印全部的
如果要一层层的打印
思路: 我们可以定义一个变量,用来统计当前队列的个数,也就是当层的节点个数,然后每出列一个就把对应的左右孩子插入进去,然后该变量减1,直到为0,也就是该层的节点全部出列了,然后再计算出队列的长度,也就是下一层的节点个数,然后继续，直到队列的长度为0

数据结构第六课 -----链式二叉树的实现,数据结构

// 层序遍历
void BinaryTreeLevelOrder(BinaryTreeNode* root)
{
	//创建一个队列
	Queue Qu;
	//初始化
	QueueInit(&Qu);
	//插入的是节点,
	if (root != NULL)
		QueuePush(&Qu, root);
	int size = QueueSize(&Qu);
	while (QueueSize(&Qu))
	{
		while (size--)
		{
			BinaryTreeNode* from = QueueFront(&Qu);


			printf("%d ", from->val);
			//删除
			QueuePop(&Qu);
			//需要注意的是删除只是释放掉存储了二叉树节点的地址的空间,并没有释放二叉树节点
			if (from->left != NULL)
			{
				QueuePush(&Qu, from->left);
			}
			if (from->rigth != NULL)
			{
				QueuePush(&Qu, from->rigth);
			}
		}
		printf("\n");
		size = QueueSize(&Qu);
		
	}
	printf("\n");
	QueueDestroy(&Qu);
	
	
	
}

判断是否是完全二叉树
思路：我们和上面的层次遍历一样，先找一个队列进行一层层的入队和出队，如果遇见节点为NULL的就判断后面是否还有节点存在

// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BinaryTreeNode* root)
{
	//创建一个队列
	Queue Qu;
	//初始化
	QueueInit(&Qu);
	//插入的是节点,
	if (root != NULL)
		QueuePush(&Qu, root);
	while (QueueSize(&Qu))
	{
		
		BinaryTreeNode* from = QueueFront(&Qu);
		if (from == NULL)
			break;
		//删除
        QueuePop(&Qu);
		//需要注意的是删除只是释放掉存储了二叉树节点的地址的空间,并没有释放二叉树节点
		QueuePush(&Qu, from->left);
		QueuePush(&Qu, from->rigth);
	}
	//判断后面是否还有非空
	while (!QueueEmtry(&Qu))
	{
		BinaryTreeNode* from = QueueFront(&Qu);
		if (from != NULL)
			return 0;
		//删除
		QueuePop(&Qu);
	}
	QueueDestroy(&Qu);
	return 1;

}