一、多维数组
(一)数组的定义
数组是由n(n≥1)个相同数据类型的数据元素组成的有限序列,在定义数组时,会为数组分配一个固定大小的内存空间,用来存储元素,数组在被定义后,其维度不可以被改变。
数组在确定其维度和维界后,元素的个数是固定的,所以不能进行插入和删除运算。数组中最常见的两种操作是查找和修改。
(二)二维数组
数组可分为一维数组和多维数组(常见的有二维数组),二维数组可以看作一维数组的一维数组。顺序表是一个一维数组,所以它是线性结构,与栈、队列、串的逻辑结构相同,而多维数组则是典型的非线性结构,也可以说它是嵌套的线性结构。
例如,一个二维数组A[3][4]在内存中实际上是一个长度为3的一维数组,每个元素是一个长度为4的一维数组,即对应三行四列,其中元素是从上到下、从左到右依次存储的,如下:
| 0 | 1 | 2 | 3 | |
|---|---|---|---|---|
| 0 | [0,0] | [0,1] | [0,2] | [0,3] |
| 1 | [1,0] | [1,1] | [1,2] | [1,3] |
| 2 | [2,0] | [2,1] | [2,2] | [2,3] |
由于数组中是从下标0开始的,所以一个m行n列的二维数组中,最开始的元素是[0,0],最后的元素是[m-1,n-1],上面三行四列的二维数组A[3][4]中的最后一个元素即为[2,3]。
(三)多维数组的存储
二维数组的存储较一维数组不一样,有两种存储方式,可分为行优先存储和列优先存储,前者是先按每行存储满后再继续下一行,后者相反先按每列存储满后再继续下一列。
例如,定义一个二维数组A[3][3],在连续的内存空间里,如下:
若按照行优先存储,以A[2][0]为例,在存储A[2][0]之前,是这样存储的:
而按照列优先存储,以A[1][1]为例,在存储A[1][1]之前,是这样存储的:
(四)多维数组的下标的相关计算
设一个二维数组A[i][j],其中行下标和列下标的范围分别为[0,a]和[0,b],若每个数组元素在内存中占用L个存储单元,且数组中第一个元素的存储位置为LOC[c1][c2],求该二维数组中任意一元素A[i][j]的存储位置?
1、按行优先存储
【所求行乘列界限加1,然后加所求列确定位置】
(1)先确定有多少行,加上列数,然后乘以存储单元,最后加上第一个元素的存储位置,得:LOC[i][j]=LOC[c1][c2]+[(i-c1)×(b-c2+1)+(j-c2)]×L。
(2)若在编程语言中,由于数组元素下标是从0开始的,该式子改写为:LOC[i][j]=LOC[0][0]+[i×(b+1)+j]×L。
例、二维数组A[m][n]采用行序为主方式存储,每个元素占L个存储单位。元素A[0][0]的存储地址是b,求元素A[i][j](0 ≤ i ≤ m-1,0 ≤ j ≤ n-1)的存储地址。
解析:由于二维数组中行列元素都是从0开始的,即LOC[i][j]=b+[i×(n-1+1)+j]×L=b+[i×n+j]×L。
2、按列优先存储
【所求列乘行界限加1,然后加所求行确定位置】
(1)先确定有多少列,加上行数,然后乘以存储单元,最后加上第一个元素的存储位置,得:LOC[i][j]=LOC[c1][c2]+[(j-c1)×(a-c2+1)+(j-c1)]×L。
(2)若在编程语言中,由于数组元素下标是从0开始的,该式子改写为: LOC[i][j]=LOC[0][0]+[j×(a+1)+i]×L。
例、设7行6列的数组a以列序为主序顺序存储,基地址为1024,每个元素占2个存储单元,架设无第0行第0列,求第4行第5列的元素的存储地址。
解析:由于第一个元素为a[1][1],所以要减去后再代入计算,即
LOC[4][5]=1024+[(5-1)×(7-1+1)+(4-1)]×2=1024+62=1086。
- 对于一个数组An×n(方阵),其元素aij按行优先与按列优先存储时地址之差为(n-1)(i-j)。
二、矩阵
(一)特殊矩阵和稀疏矩阵
相同的元素或零元素在矩阵中的分布存在一定规律的矩阵称为特殊矩阵,反之则为稀疏矩阵。简单的来说,特殊矩阵既然特殊,说明其中有很多相同或者有零元素,且存在一定规律在矩阵中分布。
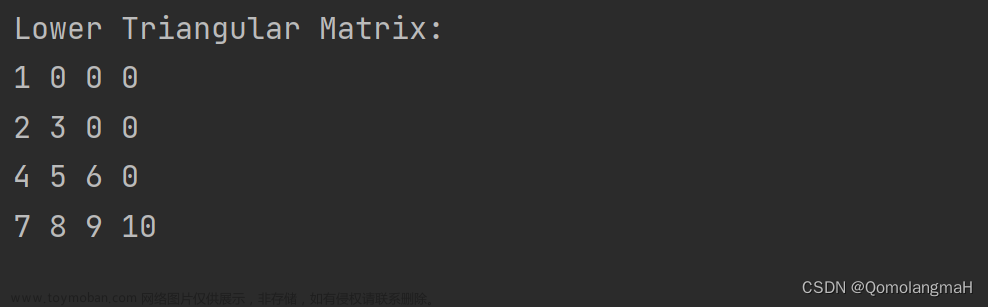
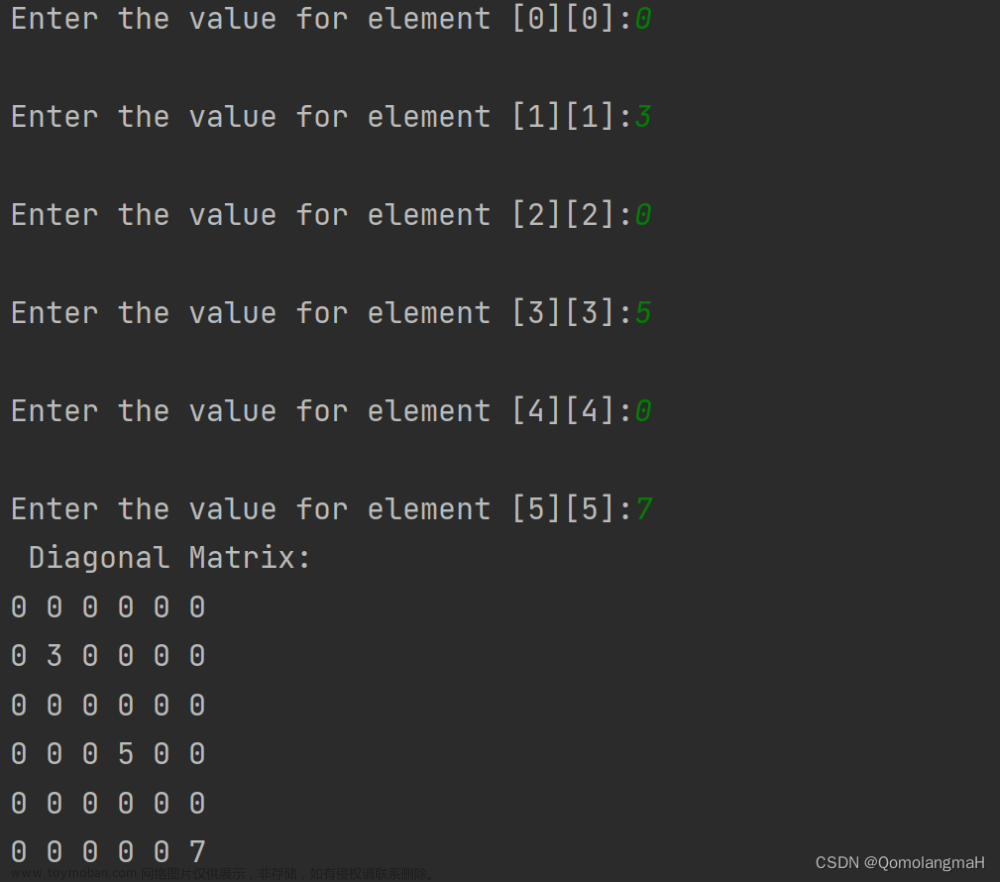
常见的特殊矩阵有对称矩阵、反对称矩阵、上/下三角矩阵、对角矩阵等等,例如对角矩阵中,只有对角线上有元素,其余元素均为零:
(二)对称矩阵及其压缩存储
若一个n阶方阵满足Ai×j=Aj×i,则称为对称矩阵。由于对称矩阵中上三角部分和下三角部分的元素对应相同,在存储对称矩阵时,为了避免空间的浪费,可以只存储上或下三角部分的元素,将其存放在一个一维数组中,数组的大小为1+2+……+n=n(1+n)/2。
例如,矩阵B如下,将其视为一个对称矩阵:
若对其进行压缩存储,若按行序将元素通过一维数组存储实现,首先确定数组大小,由于矩阵是4×4的方阵,阶数为n=4,所以需要的一维数组大小为n(1+n)/2=(4×5)/2=10,由于是对称矩阵,只存储上或下三角部分的元素,这里以存储上三角元素为例:
(三)对角矩阵
三对角矩阵就是一种对角矩阵,其中非零元素都集中在以主对角线为中心的三条对角线的区域中,其他区域均为零。
(四)稀疏矩阵的压缩存储
前面讲到,稀疏矩阵中非零元素的分布与特殊矩阵相反,是没有规律的。稀疏矩阵中大部分元素都为0,且与非零元素的分布一样,也是没有规律的。对矩阵压缩的目的是节省存储空间。
1、三元组表
为了压缩存储稀疏矩阵,在存储时不仅要存储矩阵中非零元素的值,同时还要存储该元素所在的行与列,从而组成一个三元组表(行、列、值),依此减少了存储空间。由于是将稀疏矩阵中的非零元素以及其对应的行、列号以三元组的形式存储在一个数组中,所以经过这种压缩存储后就无法通过数组的下标直接存取矩阵的元素,失去了随机存取的特性。另外,稀疏矩阵的三元组表也可以采用十字链表法存储。【稀疏矩阵的两种存储结构是三元组表(数组)和十字链表】
//以整型int为例,可替换其他类型
typedef struct{
int i,j; //行与列
int x; //值
}Sparsematrix;
例如,一个稀疏矩阵A,进行压缩存储:
对应的三元组表,如下:
| i(行) | j(列) | x(值) |
|---|---|---|
| 1 | 1 | 4 |
| 1 | 3 | 2 |
| 2 | 0 | 5 |
例如,有一个100×90的稀疏矩阵,非0元素有10个,设每个整型数占2字节,则用三元组表示矩阵时,求所需的字节数。
解析:三元组表包括行、列、值,每个整型数占2字节,所以10个非0元素占3×2×10=60字节,另外还有三元组表中行数、列数和总的非零元素个数共6个字节,一共60+6=66字节。文章来源:https://www.toymoban.com/news/detail-769315.html
2、十字链表
十字链表法中,稀疏矩阵的行和列都用一个带头结点的链表表示,从而对应着五个分量:行、列、数据域、指向下方结点的指针和指向右方结点的指针,其结点的结构如下: 文章来源地址https://www.toymoban.com/news/detail-769315.html
文章来源地址https://www.toymoban.com/news/detail-769315.html
到了这里,关于数据结构学习笔记——多维数组、矩阵的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!