(数据结构)普利姆算法(Prim)实现-Toy模板网

这篇具有很好参考价值的文章主要介绍了(数据结构)普利姆算法(Prim)实现。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

普利姆(Prim算法)

假设要在n个城市之间建立通信联络网，每两个城市之间建立线路都需要花费不同大小的经费，则连通n个城市只需要n-1个条线路，最小生成树解决的问题就是：如何在最节省经费的前提下建立这个通信网

也可以理解为：n个城市之间最多可以建立n(n-1)/2条线路，我们要从这里挑出n-1条线路

算法思路

下面就是普里姆算法(Prim)的大致思路：

该算法又称加点法，顾名思义就是一步一步地将顶点加入到集合U中，所以，我们需要维护一个tag数组，其中 tag[i]=true 就表示第i个顶点已被加入到集合U中

bool tag[maxn];   //标记，tag[i]=1表示顶点i在集合U中
1

同时，我们还要维护一个辅助数组closedge，用于表示 没有加入到集合U的顶点 到 已经加入到集合U的顶点 的最小权值
closedge[i] 中的 i 就是指还没有加入集合U的那个顶点，closedge[i].adjvex指的就是顶点i连接的那个已经在集合U中的顶点

struct{
	int adjvex;  //最小边在U中的那个顶点
	int lowcost;  //最小边上的权值
}closedge[maxn];
1234

下面废话不多说，直接上图

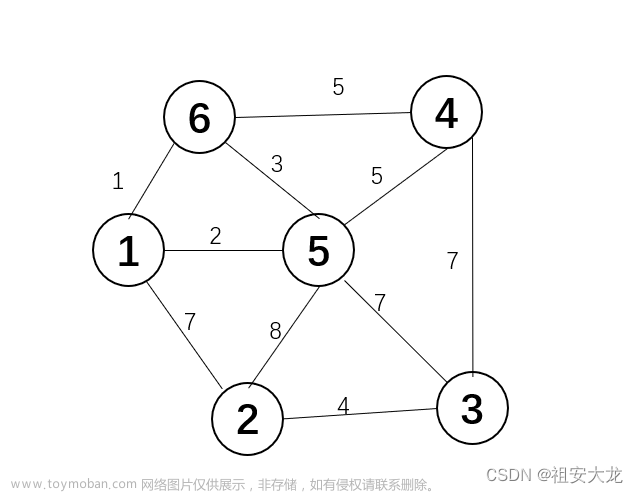
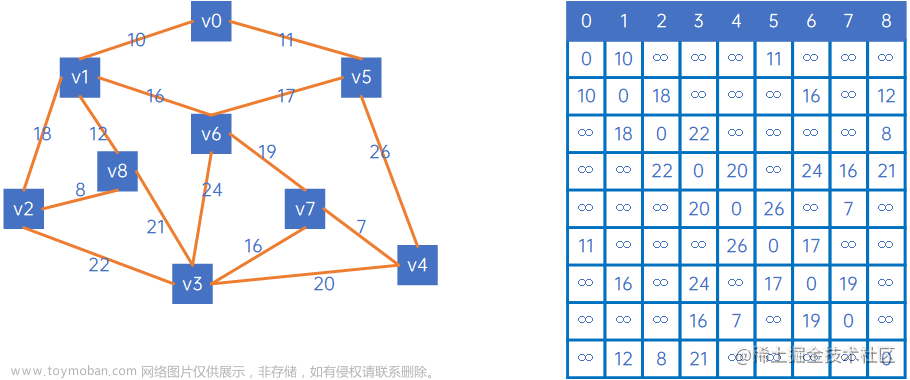
有这样的一个无向连通图，我们接下来需要求的是这个图的最小生成树
prim算法实现:“加点法”,数据结构秃头之路,算法,数据结构,图论

我们从顶点A开始，先把顶点A加入到集合U中（这里就标记为绿色了）
然后扫描与顶点A直接相连的顶点，初始化closedge
然后扫描closedge，发现C的lowcost最小，所以把C加入集合U中，产生一条边A -- C
扫描与C直接相连的顶点A B D E F
(1) A已加入集合U，忽略
(2) B与C相连的边的权值为5，比原来记录的6还要小，所以更新顶点B的adjvex为C，lowcost为5
(3) D与C相连的边的权值为5，并不比原来的小，可以跳过
(4) E和F在closedge中没有记录，直接加入即可

5.现在F的lowcost最小，把F加入到集合U，并更新closedge

6.目前D的lowcost最小，执行一样的操作

7.现在B的lowcost最小

8.剩下最后一个顶点B

所以该图的最小生成树如下图所示：

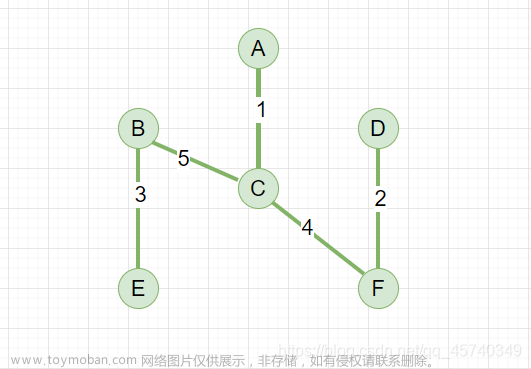
留下的5条边刚好是表格中的这5条边

文章来源地址https://www.toymoban.com/news/detail-769757.html

实现

c++邻接表存储法+再打印

c++
 #include <iostream>
 using namespace std;
 typedef long long ll;
 # define maxn 1024    //最大顶点数量
 int matrix[maxn][maxn];   //邻接矩阵
 bool tag[maxn];   //标记，tag[i]=1表示顶点i在集合U中
 int n, m;  //n:顶点个数（其中顶点标号从1到n）  m：边的个数
 struct {
 	int adjvex;  //最小边在U中的那个顶点
 	int lowcost;  //最小边上的权值
 }closedge[maxn];
 
 /*
 增加一条连接n1顶点和n2顶点的边，权值为k
 */
 void link(int n1, int n2, int k) {
 	matrix[n1][n2] = k;
 	matrix[n2][n1] = k;
 }
 
 /*
 初始化
 */
void init() {
 	//初始化邻接矩阵
 	for (int i = 0; i < maxn; ++i) {
 		for (int j = 0; j < maxn; ++j) {
 			matrix[i][j] = -1;
 		}
 	}
	memset(tag, 0, sizeof(maxn));
 	n = 6;   //一共有6个顶点
 	m = 10;   //10条边
  
  //link(0, 3, 7);
 	//link(0, 5, 3);
 	//link(0, 2, 8);
 	//link(0, 1, 5);
 	//link(1, 2, 4);
 	//link(2, 3, 5);
 	//link(2, 5, 9);
 	//link(3, 5, 6);
 	//link(3, 4, 5);
 	//link(4, 5, 1);
 	//下面m行都是在建图
	link(1, 2, 6);
 	link(1, 3, 1);
 	link(1, 4, 5);
 	link(2, 3, 5);
 	link(3, 4, 5);
 	link(2, 5, 3);
 	link(3, 5, 6);
 	link(3, 6, 4);
 	link(4, 6, 2);
 	link(5, 6, 6);
 	tag[1] = 1;   //从该顶点出发（把该顶点加入集合U）
 	//对没有加入集合U中的顶点，都初始化closedge
 	for (int i = 2; i <= n; ++i) { 		
 	  closedge[i].adjvex = 1;
 		closedge[i].lowcost = matrix[1][i];
 	}
 };
  /*
 Prim算法开始
 */
 /
 void prim() {
 	int T = n - 1;
 	//循环执行n-1次
 	while (T--) {
 		//首先寻找【不在U集合中】并且【closedge中权值最小】的边
 		int mi = 0x3f3f3f3f;   //记录当前最小的权值
 		int k = 0;   //最小权值时候的顶点
 		for (int i = 1; i <= n; ++i) {
 			if (!tag[i]/*保证不在集合U中*/ && closedge[i].lowcost != -1/*保证边存在*/ && closedge[i].lowcost < mi/*保证权值最小*/) {
 				mi = closedge[i].lowcost;
 				k = i;
 			}
 		}
 		cout << k << " --- " << closedge[k].adjvex << endl;  //找到一条边
 		tag[k] = 1;  //标记
		//更新closedge
 		for (int i = 1; i <= n; ++i) {
 			if (closedge[i].lowcost == -1/*原来的边不存在*/ || (matrix[k][i] != -1 && matrix[k][i] < closedge[i].lowcost)/*保证k--i的边存在并且比原来记录的要小*/) {
 				closedge[i].adjvex = k;
 				closedge[i].lowcost = matrix[k][i];
 			}
 		}
 
 	}
 }
/
  int main() {
 	ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
 	init();   //初始化
 	prim();
 	return 0;
 }

java直接从邻接矩阵打印

``java
 public class primAlgorithm {
 	public static void main(String[] args) {
 		//测试图是否创建成功
 		char[] data = new char[] {'A','B','C','D','E','F','G'};
 		int verxs = data.length;
 		int[][] weight = new int[][] {
			{10000,5,7,10000,10000,10000,2},
			{5,10000,10000,9,10000,10000,3},
 			{7,10000,10000,10000,8,10000,10000},
 			{10000,9,10000,10000,10000,4,10000},
 			{10000,10000,8,10000,10000,5,4},
 			{10000,10000,10000,4,5,10000,6},
 			{2,3,10000,10000,4,6,10000},
	};
 		//创建Mgraph对象
 		Mgrap mgraph = new Mgrap(verxs);
 		//创建一个MinTree对象
 		Mintree minTree = new Mintree();
 		minTree.creatGraph(mgraph, verxs, data, weight);
 		//输出
 		minTree.showGraph(mgraph);
     //测试普利姆
 		minTree.prim(mgraph, 0);
 	}
 }
 


 //创建最小生成树
 
 class Mintree{
 	/**
 	 * 
 	 * @param greap 图对象
 	 * @param verxs 图顶点个数
 	 * @param data  图顶点值
 	 * @param weight 邻接矩阵
 	 */
 	public void creatGraph(Mgrap graph,int verxs,char data[],int[][] weight ) {
 		for (int i = 0; i < verxs; i++) {
 			graph.data[i] = data[i];
 			for(int j =0; j < verxs; j++) {
 				graph.weight[i][j] = weight[i][j];
 		}
 		}
 	}
 	
 	//显示图的邻接矩阵
 	public void showGraph(Mgrap graph) {
 		for(int[] link: graph.weight) {
 			System.out.println(Arrays.toString(link));
 		}
 	}
 	
 	//编写Prim,生成最小生成树
 	/**
 	 * 
 	 * @param graph 图
 	 * @param v    表示从图的第几个顶点开始> 	 */
 	public void prim(Mgrap graph,int v) {
 		//标记tag  默认为0 其他语言不一定会初始化为0
 		int tag[] = new int[graph.verx];
 		//
 		tag[v] = 1;
 		int h1 =-1;
		int h2 =-1;
 		int minheright =100000;
 		for(int k =1;k < graph.verx; k++) {//寻找n-1次
 			//选择不在集合中 且存在的最小边
 			for(int i = 0;i<graph.verx; i++) {
 				for(int j = 0; j<graph.verx; j++) {//遍历矩阵
 					if(tag[i]==1 && tag[j] == 0 && graph.weight[i][j] < minheright) {
                         //如果当前顶点已经遍历 ,隔壁顶点没有遍历, 选出其中最小的那条
						minheright = graph.weight[i][j];
 						h1 = i;
 						h2 = j;
 					}
 				}	
 			}
 			//打印
 			System.out.println("边<"+graph.data[h1] + "," + graph.data[h2] + "> 权值:" + minheright);
 			tag[h2] = 1;
 			minheright = 10000;
 		}
 		
 	}
 }
 class Mgrap{
 	int verx;//图的节点个数
 	char[] data;//存放节点数据
 	int[][] weight;//存放边
 	public Mgrap(int verxs) {
 		this.verx =verxs;
		data = new char[verxs];
 		weight = new int[verxs][verxs];
  }
}