这篇具有很好参考价值的文章主要介绍了线性代数：为什么所有3x3对称矩阵构成的向量空间是6维的？（mit第11讲中的疑问）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。
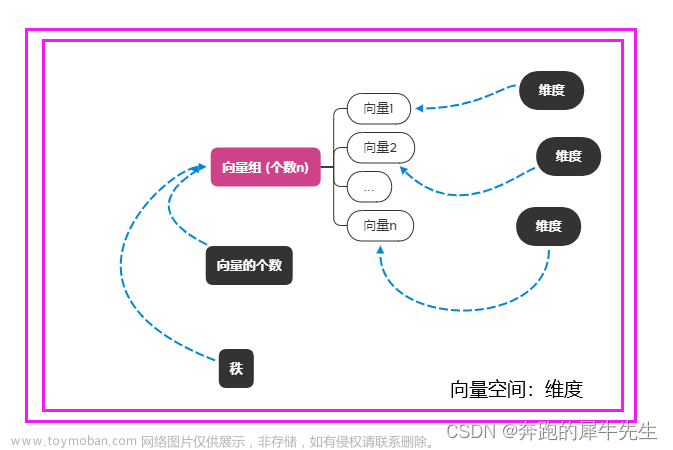
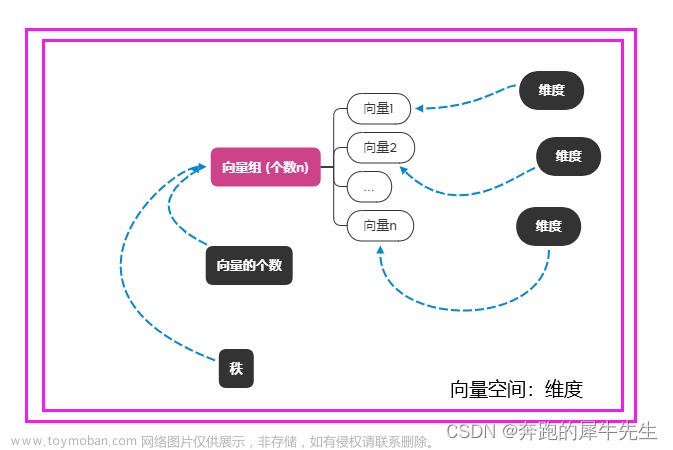
对应mit线性代数第11讲矩阵空间，秩1矩阵，小世界图第6-7分钟的讲解问题：3x3对称矩阵构成的向量空间为什么是6维的文章来源：https://www.toymoban.com/news/detail-770079.html
看了一些资料，发现这个国外的大哥讲得清楚
https://math.stackexchange.com/questions/2813446/what-is-the-dimension-of-the-vector-space-consisting-of-all-3-by-3-symmetric-mat
转成中文后如下
文章来源地址https://www.toymoban.com/news/detail-770079.html
到了这里，关于线性代数：为什么所有3x3对称矩阵构成的向量空间是6维的？（mit第11讲中的疑问）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！
目录 1 空间相关的群，环，域，集合，空间的预备知识 1.1：群，环，域，集合，空间的定义（表示不懂，只是做个标记） 2 空间 2.1 各种空间概念 3 标量空间 4 向量空间/张成空间/线性空间（vector space/ linear space） 4.1 线性空间定义 4.2 向量空间的表现 4.3 加法和数乘的封闭性
目录 0 问题引出：什么是秩？ 概念备注： 1 先厘清：什么是维数？ 1.1 真实世界的维度数 1.2 向量空间的维数 1.2.1 向量空间，就是一组最大线性无关的向量组/基张成的空间 1.3 向量α的维数 1.3.1 向量的维数=分量(数字/标量)个数 1.4 向量组/矩阵 A 的维数 1.4.1 什么是向量组的维
目录 0 问题引出：什么是秩？ 概念备注： 1 先厘清：什么是维数？ 1.1 真实世界的维度数 1.2 向量空间的维数 1.2.1 向量空间，就是一组最大线性无关的向量组/基张成的空间 1.3 向量α的维数 1.3.1 向量的维数=分量(数字/标量)个数 1.4 向量组/矩阵 A 的维数 1.4.1 什么是向量组的维
目录 0 参考的知识点和目录 1 向量 1.1 向量的概念 1.2 向量如何表示 1.3 向量/矩阵的优秀表示方法：即向量空间内的有向线段 2 矩阵 2.1 矩阵就是多个列向量的集合/合并（ 而不是 +），矩阵就是多个列向量的一种简化书写方式？ 2.2 矩阵的加法 =等价于= 向量的加法 2.3 矩阵
我们来继续探索两个多项式之间的关系，今天的研究对象是最大公因式。 一)最大公因式 因式 ：g(x)|f(x),则f(x)=h(x)*g(x)，g(x)是f(x)的 因式。 倍式：f(x)是g(x)的倍式。 最大公因式的定义如下图。 最大公因式从字面上就可以理解了，一是公因式，二是要最大的那一些，至于为什么
从大的趋势上来看，肯定是所有的企业都要拥抱大模型或者是拥抱AI的。但是目前从我们对于很多大模型的测评结果与第三方视角来看，大部分企业的核心业务、生产流程还是不太能够依赖大模型的，现在还是属于在相对边缘的业务上做一些尝试，可能成本的下降不是直接等
在面试的时候被问到一个问题，既然虚函数可以不被重写，为什么不把所有的函数都设置成虚函数？ 我当时的回答是，因为对于工程来说，一个类里可能会有很多的函数，都设置成虚函数的话会有很多不必要的开销（虚函数表）。但总觉得回答不够完善，所以闲下来去了解了
关系就是，特征值的重数 ≥ 该特征值的线性无关向量的个数 ≥ 1 量化关系有 特征值的重数，称为 代数重数 ，等于Jordan矩阵中特征值为λ的Jordan块的阶数之和 特征向量的个数，称为 几何重数 ，等于Jordan矩阵中特征值为λ的Jordan块的个数 证明 先说结论 每个矩阵 等价 于一个
1.解线性方程组 2.线性方程组解的情况 3.线性方程组的两个基本问题 1.阶梯型矩阵性质 2.简化阶梯型矩阵（具有唯一性） 3.行化简算法 4.线性方程组的解 1.R^2中的向量 2.R^2中的几何表示 3.R^n中的向量 4.线性组合与向量方程 5.span{v},span{u,v}的几何解释 1.定义 2.定理 3.解的存在性
所有笔记请看： 博客学习目录_Howe_xixi的博客-CSDN博客 https://blog.csdn.net/weixin_44362628/article/details/126020573?spm=1001.2014.3001.5502 思维导图如下： 内容笔记如下：
