Matlab拥有强大的绘图功能,内置了很多绘图函数,只需要给出一些基本参数就能得到所需图形,这类函数称为高层绘图函数。
此外,Matlab还提供了直接对图形句柄进行操作的低层绘图操作。这类操作将图形的每个图形元素(如坐标轴、曲线、文字等)看做一个独立的对象,系统给每个对象分配一个句柄,可以通过句柄对该图形元素进行操作,而不影响其他部分。

一、二维作图
定义:二维图形是将平面坐标上的数据点连接起来的平面图形。
分类:直角坐标;对数坐标;极坐标。
二维图形的绘制是其他绘图操作的基础。
1.1 plot函数的基本用法
1.1.1 直角坐标
plot函数用于绘制二维平面上的线性坐标曲线图,要提供一组x坐标和对应的y坐标,可以绘制分别以x和y为横、纵坐标的二维曲线。
用法
plot(x,y)%其中x,y为长度相同的向量,存储x坐标和y坐标示例
x=0:0.01:2*pi;
y=sin(x);
plot(x,y)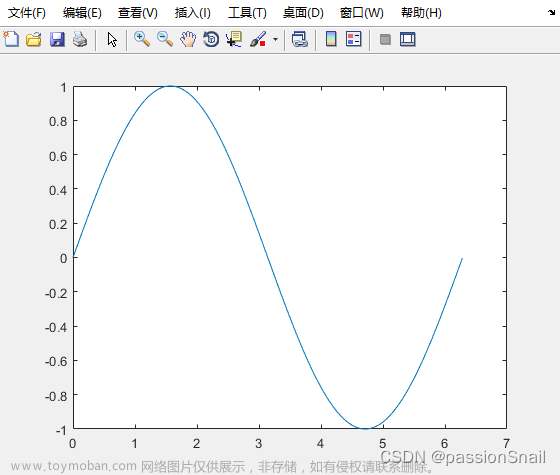
1.1.2 参数方程
参数形式给出的曲线方程,只要给定参数向量,再分别求出x, y向量即可输出曲线
示例
t=0:0.01:1;
x=t*2*pi;
y=sin(t).*cos(t);
plot(x,y)
1.1.3 同时画多条线,并考虑线型、颜色等
用法
plot(x1,y1,‘选项’,x2,y2,‘选项2’,x3,y3,‘选项3’,x4,y4,‘选项4',...)%选项格式:颜色+线型,如blueo、red-、black-o示例
x=0:0.1:3;
y1=x;
y2=x.^2;
y3=x.^3;
plot(x,y1,'red-',x,y2,'blueo',x,y3,'black-o')
1.1.4 图形标注
在绘制图形时,可以对图形加上一些说明,如图形的名称、坐标轴说明以及图形某一部分的含义等,这些操作称为添加图形标注。
用法
title(‘图的题目')
xlabel(‘横轴的名称')
ylabel(‘纵轴的名称')
text(x,y,‘说明’)
legend(‘图例1’,‘图例2’,‘图例3')示例
x=0:0.1:3;
y1=x;
y2=x.^2;
y3=x.^3;
plot(x,y1,'red-',x,y2,'blueo',x,y3,'black-o')
title('示意图')
xlabel('x的变化')
ylabel('y的变化')
text(0.5,25,'说明示例')
legend('线性y=x','二次方y=x^2','三次方y=x^3')
线型、颜色、符号可选择如下
线型 |
颜色 |
符号 |
符号 |
- 实线 |
b 蓝色 |
. 点 |
^ 上三角 |
: 虚线, |
g 绿色 |
o 圆圈 |
< 左三角 |
-. 点划线 |
r 红色 |
× 叉号 |
> 右三角 |
-- 虚线 |
c 青色 |
+ 加号 |
v 下三角 |
m 品红 |
* 星号 |
h 六角星 |
|
y 黄色 |
s 方块 |
||
k 黑色 |
d 菱形 |
||
w 白色 |
p 五角星 |
注意:这里的颜色一般都比较明亮,但是方便使用,建议大家建立自己的颜色库。
1.1.5 坐标、图形和图层窗口控制
在绘制图形时,Matlab可以自动根据要绘制曲线数据的范围选择合适的坐标刻度,使得曲线能够尽可能清晰的显示出来。所以,一般情况下用户不必选择坐标轴的刻度范围。但是,如果用户对坐标不满意,可以利用axis函数对其重新设定。
axisequal%纵横坐标轴采用等长刻度
axissquare%产生正方形坐标系(默认为矩形)
axisauto%使用默认设置
axisoff%取消坐标轴
axison%显示坐标轴
gridon%显示网格
gridoff%不显示网格
boxon%显示其他轴(上、右)
boxoff%不显示其他轴(上、右)
holdon%继续在同一图层绘图
figure(1)%新生成一个图层2.2 双纵坐标函数plotyy
在Matlab中,如果需要绘制出具有不同纵坐标标度的两个图形,可以使用plotyy函数,它能把具有不同量纲,不同数量级的两个函数绘制在同一个坐标中,有利于图形数据的对比分析。
示例
x1=0:0.01:2*pi;
x2=x1;
y1=sin(x1);
y2=cos(x1);
plotyy(x1,y1,x2,y2)
2.3 图形窗口分割
在实际应用中,经常需要在一个图形窗口中绘制若干个独立的图形,这就需要对图形窗口进行分割。分割后的图形窗口由若干个绘图区组成,每一个绘图区可以建立独立的坐标系并绘制图形。同一图形窗口下的不同图形称为子图。
用法
subplot(m,n,p)该函数把当前窗口分成m×n个绘图区,m行,每行n个绘图区,区号按行优先编号。其中第p个区为当前活动区。每一个绘图区允许以不同的坐标系单独绘制图形。
示例
x=0:0.1:2*pi;
y1=sin(x);
y2=cos(x);
y3=tan(x);
y4=sin(x).*cos(x);
subplot(2,2,1)
plot(x,y1,'blacko')
subplot(2,2,2)
plot(x,y2,'ro')
subplot(2,2,3)
plot(x,y3,'bo')
subplot(2,2,4)
plot(x,y4,'go')
2.4 其他形式的线性直角坐标图
条形图 bar(x,y)
阶梯图 stairs(x,y)
杆图 stem(x,y)
填充图 fill(x,y)
fill函数按向量元素下标渐增次序依次用直线段连接x,y对应元素定义的数据点。
示例
x=0:0.35:7;
y=2*exp(-0.5*x);
subplot(2,2,1);
bar(x,y,'g');
title('bar(x,y,''g'')');
axis([0,7,0,2]);
subplot(2,2,2);
fill(x,y,'r');
title('fill(x,y,''r'')');
axis([0,7,0,2]);
subplot(2,2,3);
stairs(x,y,'b');
title('stairs(x,y,''b'')');
axis([0,7,0,2]);
subplot(2,2,4);
stem(x,y,'k');
title('stem(x,y,''k'')');
axis([0,7,0,2]);
2.5 极坐标图

polar函数用来绘制极坐标图
用法
polar(theta,rho,'options')theta为极坐标极角,rho为极径,选项的内容和plot函数相似。
示例
theat=0:0.1:4*pi;
y1=sin(1/2*theat);
y2=sin(theat).*cos(theat);
subplot(2,2,1)
plot(theat,y1,'ro')
subplot(2,2,2)
plot(theat,y2,'b-')
subplot(2,2,3)
polar(theat,y1,'ro')
grid on
subplot(2,2,4)
polar(theat,y2,'b-')
grid on
2.6 对数坐标图
x轴线性,y轴线性
plot(x,y)x轴对数,y轴线性
semilogx(x,y)x轴线性,y轴对数
semilogy(x,y)x轴对数,y轴对数
loglog(x,y)示例
x=1:1000;
y=x.^2+exp(x);
subplot(2,2,1)
plot(x,y,'r-')
subplot(2,2,2)
semilogx(x,y,'b-')
subplot(2,2,3)
semilogy(x,y,'m-')
subplot(2,2,4)
loglog(x,y,'k-')
2.7 符号函数
显函数
ezplot('f(x)',[a,b])隐函数
ezplot('f(x,y)',[xmin,xmax,ymin,ymax])参数方程
ezplot('x(t)','y(t)',[tmin,tmax])示例1
subplot(3,1,1)
ezplot('sin(x)',[0,2*pi])
subplot(3,1,2)
ezplot('exp(x)+sin(x*y)',[-2,2,-1000,1000])
subplot(3,1,3)
ezplot('3*t','sin(t)*cos(t)',[0,2*pi])
示例2
ezplot('x+exp(-x*y)+sin(x*y)',[0,1,0,600])
二、三维作图
空间曲线
空间曲面
2.1 空间曲线
plot3函数
类似plot2,用法一致
用法:一条
plot3(x,y,z,'options')用法:多条
plot3(x1,y1,z1,'options1',x2,y2,z2,'options2',...)示例1
x=1:0.1:10;
y=1:0.1:10;
z=x.^2+y;
plot3(x,y,z,'r-o')
grid on
示例2:参数
t=0:pi/50:10*pi;
y1=sin(t);
y2=cos(t);
plot3(y1,y2,t,'ro');
grid on
示例3
x=-3:0.2:3;
y=1:0.2:5;
[X,Y]=meshgrid(x,y);
Z=(X+Y).^2;
subplot(2,2,1)
plot3(X,Y,Z)
subplot(2,2,2)
plot3(X,Y,Z)
shadingflatx=-3:0.1:3;
y=1:0.1:5;
[X,Y]=meshgrid(x,y);
Z=(X+Y).^2;
subplot(2,2,3)
plot3(X,Y,Z)
subplot(2,2,4)
plot3(X,Y,Z)

2.2 空间曲面
surf函数
用法
surf(x,y,z)示例
x=-3:0.2:3;
y=1:0.2:5;
[X,Y]=meshgrid(x,y);
Z=(X+Y).^2;
subplot(2,2,1)
surf(X,Y,Z)
subplot(2,2,2)
surf(X,Y,Z)
shadingflatx=-3:0.1:3;
y=1:0.1:5;
[X,Y]=meshgrid(x,y);
Z=(X+Y).^2;
subplot(2,2,3)
surf(X,Y,Z)
subplot(2,2,4)
surf(X,Y,Z)
mesh函数
用法
mesh(x,y,z)示例1
x=-3:0.2:3;
y=1:0.2:5;
[X,Y]=meshgrid(x,y);
Z=(X+Y).^2;
subplot(2,2,1)
mesh(X,Y,Z)
subplot(2,2,2)
mesh(X,Y,Z)
shadingflatx=-3:0.1:3;
y=1:0.1:5;
[X,Y]=meshgrid(x,y);
Z=(X+Y).^2;
subplot(2,2,3)
mesh(X,Y,Z)
subplot(2,2,4)
mesh(X,Y,Z)
示例2
m=30;
z=1.2*(0:m)/m;
r=ones(size(z));
theta=(0:m)/m*2*pi;
x1=r'*cos(theta);
y1=r'*sin(theta);
z1=z'*ones(1,m+1);
x=(-m:2:m)/m;
x2=x'*ones(1,m+1);
y2=r'*cos(theta);
z2=r'*sin(theta);
surf(x1,y1,z1);
axis equal
axis off
hold on
surf(x2,y2,z2);
axis equal
axis off
hold off
还有两个和mesh函数相似的函数,即带等高线的三维网格曲面函数meshc和带底座的三维网格曲面函数meshz,其用法和mesh类似。不同的是,meshc还在xy平面上绘制曲面在z轴方向的等高线,meshz还在xy平面上绘制曲面的底座。
surf函数也有两个类似的函数,即具有等高线的曲面函数surfc和具有光照效果的曲面函数surfl。
示例
[x,y]=meshgrid(-8:0.5:8);
z=sin(sqrt(x.^2+y.^2))./sqrt(x.^2+y.^2+eps);
subplot(2,2,1);
meshc(x,y,z);
subplot(2,2,2);
meshz(x,y,z);
subplot(2,2,3);
surfc(x,y,z);
subplot(2,2,4);
surfl(x,y,z);
2.3 标准三维曲面
Matlab提供了一些函数用于绘制标准三维曲面,这些函数可以产生相应的绘图数据,常用于三维图形的演示。如,sphere函数和cylinder函数分别用于绘制三维球面和柱面。
用法
[x,y,z]=sphere(n); %n越大,越平滑
[x,y,z]=cylinder(R,n)示例
[x,y,z]=sphere(100);
subplot(2,2,1)
mesh(x,y,z)
grid on
axis equal
subplot(2,2,2)
mesh(3*x,y,3*z)
axis equal
grid on
subplot(2,2,3)
mesh(5*x,y,z)
axis equal
grid on
subplot(2,2,4)
mesh(x,6*y,z)
axis equal
grid on
示例2
[x,y,z]=cylinder(5,200);
subplot(2,2,1)
mesh(x,y,z)
axis equal
grid on
subplot(2,2,2)
mesh(z,y,x)
axis equal
grid on
subplot(2,2,3)
mesh(x,5*y,5*z)
axis equal
grid on
t = 0:0.1:pi;
[x,y,z]=cylinder(sin(t),200);
subplot(2,2,4)
mesh(x,y,z)
axis equal
grid on
2.4 其他三维图形
在介绍二维图形时,曾经提到条形图、杆图、饼图和填充图等特殊图形,它们还可以以三维形式出现,其函数分别为bar3,stem3,pie3和fill3
subplot(2,2,1);
bar3(rand(4));
subplot(2,2,2);
y=2*sin(0:pi/10:2*pi);
stem3(y);
subplot(2,2,3);
pie3([2347,1827,2043,3025]);
subplot(2,2,4);
fill3(rand(3,5),rand(3,5),rand(3,5),'r');
常用的图形还有瀑布图和三维曲面的等高线图。绘制瀑布图用waterfall函数,用法和meshz函数相似,只是它的网格线在x轴方向出现,具有瀑布效果。
示例
x = 0:0.1:5*pi;
y = 0:0.1:5*pi;
[X Y] = meshgrid(x,y);
Z = cos(X)+sin(Y);
subplot(2,2,1)
mesh(X,Y,Z)
axis equal
grid on
subplot(2,2,2)
surf(X,Y,Z)
axis equal
grid on
subplot(2,2,3)
contour3(X,Y,Z,20,'b')
axis equal
grid on
subplot(2,2,4)
waterfall(X,Y,Z)
axis equal
grid on
2.5 三维图形的精细处理:方位角
在日常生活中,从不同的角度观察物体,所看到的物体形状是不一样的。同样,从不同视点绘制的三维图形的形状也是不一样的。视点位置可由方位角和仰角表示。
Matlab提供了设置视点的函数view,其调用格式为:view(az,el) 其中az为方位角,el为仰角,它们均以度为单位。系统默认的视点定义为方位角为-37.5度,仰角30度。
示例
subplot(2,2,1);mesh(peaks);
view(-37.5,30);
title('1');
subplot(2,2,2);mesh(peaks);
view(0,90);
title('2');
subplot(2,2,3);mesh(peaks);
view(90,0);
title('3');
subplot(2,2,4);mesh(peaks);
view(-7,-10);
title('4');
2.6 三维图形的精细处理:颜色、裁剪
Matlab定义的NaN常数可以用于表示那些不可使用的数据,利用这些特性,可以将图形中需要裁剪部分对应的函数值设置成NaN,这样在绘制图形时,函数值为NaN的部分将不显示出来,从而达到对图形进行裁剪的目的。例如,要削掉正弦波顶部或底部大于0.5的部分。
示例
x=0:pi/50:4*pi;
y=sin(x);
i=find(abs(y)>0.5);
x(i)=NaN;
figure(1)
plot(x,y,'bo');
x1 = 0:pi/50:4*pi;
y1 = sin(x1);
hold on
plot(x1,y1,'r-')
示例
[x,y,z]=sphere(25); %生成大球
z1=z;
z1(:,1:4)=NaN;%裁剪
c1=ones(size(z1)); %生成小球
surf(3*x,3*y,3*z1,c1);
hold on
z2=z;
c2=2*ones(size(z2));
c2(:,1:4)=3*ones(size(c2(:,1:4)));
surf(1.5*x,1.5*y,1.5*z2,c2);
colormap([0 1 0;0.5 0 0;1 0 0]);
grid on
hold off
三、高级绘图
3.1 高级绘图
pause用法,人为地让图动起来
用法
pause(n)%n为延迟的秒数示例
for i=0:0.1:2*pi
pause(0.1)
hold on
plot(i,sin(i),'ro')
hold on
plot(2*pi-i,cos(i),'b*')
end
3.2 动画制作
如果把MATLAB产生的多幅图保存起来,并利用系统提供的函数进行播放,就可以产生动画效果。系统所提供的动画功能有getframe,moviein和movie
lgetframe:将当前图形窗口作为一个画面取下并保存,格式为m=getframe
lmoviein:用来建立一个足够大的n列的矩阵m,用来保存n幅画面数据,以备播放
lmovie(m,n,q):以每秒n幅图形的速度播放由矩阵m的列向量组成的画面
示例1
m = moviein(20);
for j=1:20
plot(fft(eye(j+10)))
m(:,j) = getframe;
end
movie(m,2)
示例2
n = 30;
[x,y,z] = sphere(50);
m = moviein(n);
for j=1:n
surf(j*x,y,z)
axis equal
m(:,j)=getframe;
end
movie(m,1,2)
四、更加高级
在科研中,如何制作符合期刊的图非常重要
示例
数据是我的科研数据
clc
clear all
close all
a = [0.10828 236.63879
0.08265 331.08886
0.06741 371.30872
0.05578 437.27358
0.05426 441.22836
0.05176 456.26014
0.05213 513.8591
0.04897 608.83572
0.04505 610.50548
0.03615 683.223
0.03425 700.79885
0.03297 702.7128
0.03099 726.20644
0.02984 747.45412
0.0282 747.60401
0.03293 749.04588
0.03036 768.58932
0.02578 838.07791
0.03224 851.6837
0.02718 883.41168
0.03078 909.02015
0.02526 931.38886
0.02777 944.42062
0.02442 948.2596
0.02794 984.1989
0.02437 984.78035
0.02809 1007.26461
0.02213 1040.07975
0.02618 1053.19256
0.02434 1054.45237
0.02135 1107.43701
0.02078 1277.24479
0.01971 1295.3802
0.01726 1350.43554
0.01853 1361.12137
0.01621 1361.4124
0.01893 1381.69295
0.0158 1435.40845
0.01655 1437.24735
0.01694 1473.8802
0.016 1526.53607
0.01398 1574.92828
0.01373 1581.95475
0.01613 1689.83356
0.01466 1700.40832
0.01485 1706.97971
0.01413 1737.07354
0.01274 1743.87164
0.01332 1803.53878
0.01349 1887.5225
0.01147 1982.18789
0.01302 1983.09056
0.01088 2001.96919
0.01334 2051.23485
0.01123 2051.69277
0.01082 2226.89165
0.01158 2326.01969
0.00956 2421.35485
0.01023 2560.80794
0.00821 2598.375
0.00907 2761.51772
0.00933 2835.00734
0.00822 2998.28911
0.00781 3011.57692
0.00677 3040.98231
0.00597 3268.96891
0.0071 3278.60326
0.00662 3309.47982
0.00715 3397.19838
0.00748 3444.97805
0.00669 3445.27918
0.00658 3501.84261
0.00624 3884.10594
0.00526 4292.16983
0.0055 4483.02517
0.00488 4523.12293
0.00431 4529.43573
0.00487 4783.29326
0.00453 5142.53594
0.00412 5513.36257
0.00431 6029.15164
0.00445 6151.86742
0.00393 6232.48762
0.0039 6455.0746
0.00376 6498.42702
0.00317 6528.17409
0.00314 6974.12006
0.00317 7249.73053
0.00341 7591.97577
0.00379 7641.39115
0.00333 8122.37838
0.00291 8793.77312
0.0021 10059.60424
0.00212 11642.80526
0.0019 12215.83171
0.00221 12231.40193
0.00147 15957.12422
0.00091 25939.46874];
b = [0.00001 2.4E6
100000 0.00024];
figure(1)
loglog(a(:,1), a(:,2), 'o', 'MarkerSize', 8, 'color', [0 0.444 0.744], 'linewidth', 2)
xlim([5e-4, 0.2])
hold on
loglog(b(:,1), b(:,2), '--', 'linewidth', 3, 'color', [0.95 0.30 0])
ylim([1e2, 1e5])
set(gca, 'FontSize', 12)
xlabel({'$$Re_p$$'}, 'interpreter', 'latex', 'FontSize', 15)
ylabel({'$$C_D$$'}, 'interpreter', 'latex', 'Fontsize', 15)
legend({'$$\rm Experiment$$', '$${\rm Stokes}, C_D=\frac{24}{Re_p}$$'}, 'interpreter', 'latex', 'FontSize', 12, 'box', 'off')
% legend('Experiment', 'Stokes')
几点细节,非常重要
除了线型、颜色、符号,用 MarkerSize 控制符号大小,用 linewidth 控制线宽,用 FontSize 控制字体大小文章来源:https://www.toymoban.com/news/detail-770162.html
用Tex写字体,这个非常适合发表物理、数学类期刊,强烈强烈建议文章来源地址https://www.toymoban.com/news/detail-770162.html
到了这里,关于MATLAB科学绘图-MATLAB画图技巧与实例(一):常用函数的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!