【算法详解 | DFS算法】深度优先搜索解走迷宫问题

这篇具有很好参考价值的文章主要介绍了【算法详解 | DFS算法】深度优先搜索解走迷宫问题 | 深度优先图遍历。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

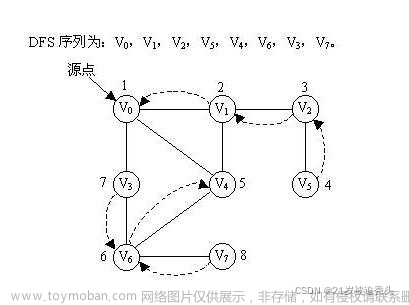
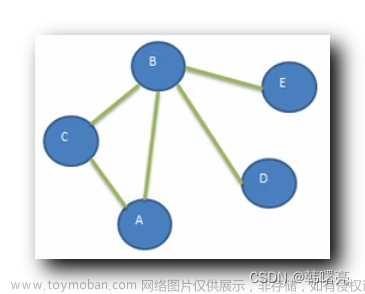
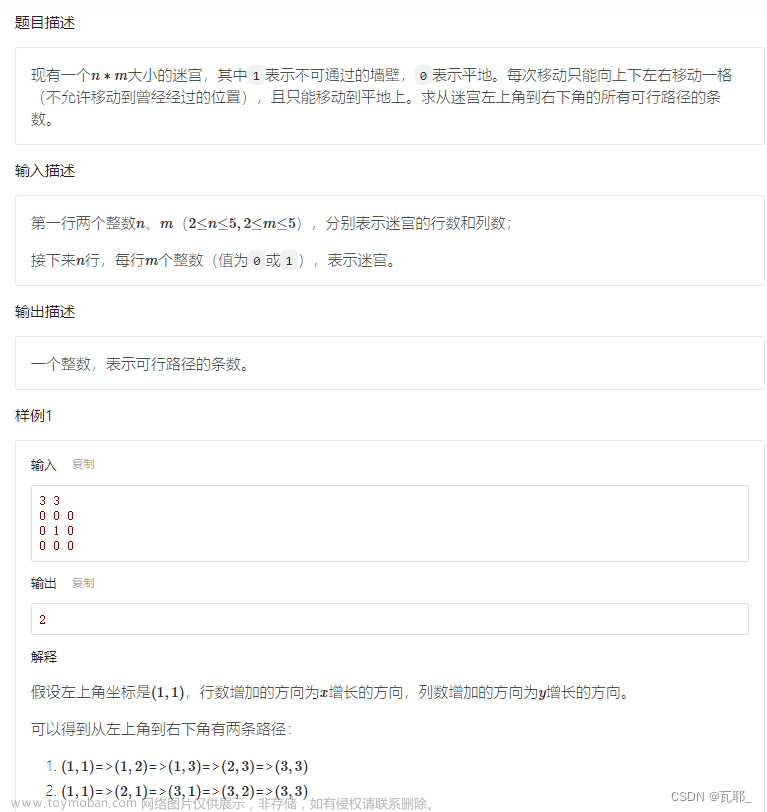
DFS算法

by.Qin3Yu

本文需要读者掌握 结构体 和栈的操作基础，完整代码将在文章末尾展示。
特别声明：本文为了尽可能使用简单描述，以求简单明了，可能部分专有名词定义不准确。

栈相关操作可以参考我的往期博文：
【C++数据结构 | 栈速通】使用栈完成十进制数转二四八进制数.by.Qin3Yu

文中所有代码使用 C++ 举例，且默认已使用std命名空间：

using namespace std;

概念速览

什么是DFS算法？

DFS，即深度优先搜索（Depth-First Search）是一种常用的图遍历算法。它通过从起始节点开始，沿着一条路径尽可能深地探索图的节点，直到达到不能继续前进的叶子节点，然后回溯到前一个节点继续探索其他路径，如下图所示：

山洞寻宝图深度优先算法 dfs,算法详解,算法,深度优先,dfs,图搜索,图论,图搜索算法,c++

图中黑色代表迷宫的墙体（障碍）；白色代表通道；绿色越深，代表搜索的顺序越靠前；灰色代表被回溯的路径。

具体步骤如下：

选择一个起始节点标记为已访问,并开始搜索他的其中一个相邻结点为新的起始节点;

重复第一步，直到走到一个叶子结点（即路径最深处，没有相邻点的点）；

如果地图中还存在未访问的结点，则回溯到上一个结点；

重复第三步，直到回溯到含有未访问相邻结点的结点，并访问此相邻结点；

重复前四步，如果回溯到起始节点并且已访问过所有节点，则搜索结束。

DFS 的特点是优先探索深度而不是广度。它会尽可能深地搜索每一个路径，直到找到目标节点或者遍历完所有节点。通过使用栈来保存遍历过程中的节点。

什么是BFS算法？

与深度优先搜索相反，BFS采用的是广度优先搜索，他的基本思想是像细菌扩张一样，从终点向外逐层扩张，直到找到终点或将全图遍历一遍。

关于BFS算法的详细解释可以参考我的往期博文，本文将不作赘述：
【C++数据结构 | 队列速通】图解BFS算法走迷宫最短路径问题.by.Qin3Yu

DFS的优势与劣势

DFS与同作为图算法的BFS相比，具有以下特点：

优势：

简单： 实现简单，容易理解和实现。

高效： 对于深度优先搜索问题，DFS 往往能够更快地找到可行解。

节省内存： 在搜索树比较深且解比较分散时，DFS 的内存消耗最少。

缺点：

无法解最优路径： DFS不一定能够找到最短路径，因为它不考虑距离和路径长度，但BFS则可以。

死循环风险： 如果图中有环状路径，DFS将陷入无限循环，因此需要保证节点的独特性，BFS则不会。

在实际应用中，我们通常需要求出最优（最短）路径，且我们不能保证地图中没有环状路径，因此我们通常认为：在绝大部分情况下BFS比DFS更优。

DFS算法详解

初始化迷宫地图

既然要走迷宫，那么就要先有迷宫地图。在本题中，题目要求使用10×10规格的地图，但此处为了便于讲解，我们使用4×4规格的地图，原理都是相同的。若要改为10×10规格，改变对应变量即可（详见结尾代码）。
在上面的地图中，每个格子代表一个点，用对应的字母表示，A为起点，P为终点，白色代表可通行路径，黑色代表障碍物。
如何用代码实现以上地图结构？遵循搜索算法五要素：

遍历范围：迷宫的大小；

初始点和目标点：即迷宫的起点和终点；

搜索方向：在本例中，我们搜索上下左右四个方向，通常情况下也是如此；

访问标记：即是否已经访问过需要访问的位置；

父结点 ：即我是因为访问了哪个节点，才需要访问这个结点，除起点外所有结点都有对应的父结点。

1. 遍历范围

int maze[4][4] = {
    {0, 1, 0, 0},
    {0, 0, 0, 1},
    {1, 0, 1, 1},
    {0, 0, 0, 0},};

山洞寻宝图深度优先算法 dfs,算法详解,算法,深度优先,dfs,图搜索,图论,图搜索算法,c++

2. 父结点

// 定义节点结构体
struct Node
{
    int x;
    int y;
    int parent;  // 记录父节点在栈中的索引
};

如图所示，访问点 A 后要访问点 B ，所以 A 为 B 的父结点

山洞寻宝图深度优先算法 dfs,算法详解,算法,深度优先,dfs,图搜索,图论,图搜索算法,c++

3. 初始点和目标点

Node start = { 0, 0, -1};  // 设置起点
Node end = { 3, 3, -1};  // 设置终点
// 终点和起点没有父结点，所以设置父结点索引为-1

4. 搜索方向

// 用二维数组表示方向，分别对应上下左右四个方向，后文称为方向数组
int directions[4][2] = { { -1, 0}, { 0, 1}, { 1, 0}, { 0, -1} };

5. 访问标记

// 用二维数组记录是否访问，地图上的每个点都对应一个bool值
bool visited[4][4] = { false };

算法结构

在走迷宫时，我们需要在搜索路径前先判断是否已经到终点，若不是则继续搜索，直到搜索到死胡同里，我们在回头至上一个岔路口，因此整体的算法结构如下：

while (bool){
    // 终点处理
    // 结点访问
    // 路径回溯
}

但下文为了使读者便于理解，不会根据此顺序讲解，读者只需知道三个部分的先后顺序即可。

访问结点

访问结点包含以下几个步骤：

根据当前结点算出下一个结点的位置；

访问下一个结点，，记录下结点的位置，并标记为已访问。

在下面的代码中，我们还要考虑一个额外因素：如何知道所有可能的路径都被访问过？
对此，我们用以下方法解决：

先默认已访问全图；

开始搜索当前结点的相邻结点，如果还有相邻结点未被搜索，则搜索结点，并标记未访问全图；

若没有相邻结点未被搜索，则回溯路径，若直到回溯至终点，仍然标记为已访问全图，则说明全图均已被访问。

因为后文需要做路径回溯的处理，所以拥有先进后出特性的栈最适合用于存放路径，具体代码示例如下：

bool has_unvisited = false;  // 定义布尔型变量，标记是否还有未访问的节点
for (int i = 0; i < 4; i++)  // 枚举上、右、下、左四个方向
{
    int next_x = current.x + directions[i][0];
    int next_y = current.y + directions[i][1];
    if (next_x >= 0 && next_x < 4 && next_y >= 0 && next_y < 4
        && maze[next_x][next_y] == 0 && !visited[next_x][next_y])  // 判断是否是合法的下一个节点
    {
        Node next_node = { next_x, next_y, path.size() };  // 创建下一个节点
        visited[next_x][next_y] = true;  // 标记下一个节点为已访问
        path.push(next_node);  // 将下一个节点入栈
        has_unvisited = true;  // 更新变量
        break;
    }
}

路径回溯

在上文中，我们使用栈来保存路径，根据栈先进后出的特性，我们回溯路径只需把最后一步弹出即可：

山洞寻宝图深度优先算法 dfs,算法详解,算法,深度优先,dfs,图搜索,图论,图搜索算法,c++

如上图所示，我们走到“死胡同” E 点以后，开始将栈中的路径弹出，一直弹出至当前点还有未访问的相邻点则停止回溯，继续访问此未访问的结点，代码如下：

if (!has_unvisited)  // 如果没有未访问的节点，就弹出当前节点
{
    path.pop();
}

终点处理

打印路径

根据上文所述，如果当前点回溯到了起始点，即栈为空，则代表已经遍历过全图，无法找到搜索到终点：

while (!path.empty()){
    // 终点处理
    // 结点访问
    // 路径回溯
}
cout << "未找到可行路径！" << endl;

另一种可能，如果当前点的坐标等于终点的坐标，则代表已经找到终点，我们只需要将路径回溯打印出即可，具体操作为将栈内元素逐个打印并弹出，原理如下图所示：

山洞寻宝图深度优先算法 dfs,算法详解,算法,深度优先,dfs,图搜索,图论,图搜索算法,c++

从图中可以看出，根据先进后出的原则，栈内元素被逐个打印后获得的路线应该是从终点到起点的路线：

Node current = path.top();  // 取出栈顶节点
if (current.x == end.x && current.y == end.y)  // 如果找到终点，就输出路径
{
    cout << "路径如下：" << endl;
    while (!path.empty())
    {
        Node node = path.top();
        cout << "(" << node.x << "," << node.y << ") ";
        path.pop();
    }
    cout << endl;
    return;
}

如果您不在乎路线的正反，则到这里全文就结束了。

反转路径

如果想将顺序颠倒过来，变成从起点到终点的路径，我们也可以用通过使用一个辅助栈来实现，原理如下图所示：

山洞寻宝图深度优先算法 dfs,算法详解,算法,深度优先,dfs,图搜索,图论,图搜索算法,c++

具体实现如下：

if (current.x == end.x && current.y == end.y)  // 如果找到终点，就输出路径
{
    cout << "路径如下：" << endl;

    stack<Node> reversepath;  // 声明一个辅助栈，用来保存反转后的顺序
    while (!path.empty())
    {
        reversepath.push(path.top());
        path.pop();
    }

    while (!reversepath.empty())  // 打印辅助栈中的内容
    {
        Node node = reversepath.top();
        cout << "( " << node.x << " , " << node.y << " ) ";
        reversepath.pop();
    }
    cout << endl;
    return;
}

至此，DFS算法讲解完毕（=

完整项目代码

题目：使用代码走出一个规格为（ n × m ）的迷宫，并返回最短路径和其步数。
ps.本文用规格为（ 10 × 10 ）的迷宫举例，需要其他规格只需修改代码内相应变量即可。

如需提问，可以在评论需留言或私信，通常在12小时内回复。不收费，用爱发电（=文章来源地址https://www.toymoban.com/news/detail-770353.html

#include <iostream>
#include <stack>
using namespace std;

// 定义迷宫地图，0 表示可以通行，1 表示障碍物
int maze[10][10] = {
    {0, 0, 1, 0, 0, 0, 1, 0, 1, 0},
    {0, 0, 1, 0, 0, 0, 0, 0, 1, 0},
    {0, 0, 0, 0, 1, 1, 0, 1, 1, 0},
    {0, 1, 1, 1, 0, 0, 0, 1, 0, 0},
    {0, 0, 0, 1, 0, 0, 0, 0, 0, 0},
    {0, 1, 0, 0, 0, 1, 0, 1, 1, 0},
    {0, 1, 1, 1, 1, 0, 0, 1, 1, 0},
    {0, 1, 0, 0, 0, 0, 1, 0, 0, 0},
    {0, 0, 0, 1, 1, 0, 1, 0, 1, 0},
    {0, 1, 1, 1, 0, 0, 0, 0, 1, 0}
};

// 定义方向数组，顺序为上、右、下、左
int directions[4][2] = { {-1,0}, {0,1}, {1,0}, {0,-1} };

// 定义节点结构体
struct Node{
    int x;
    int y;
    int parent;  // 记录父节点在栈中的索引
};

// 定义寻找最短路线的函数
void DFS(Node start, Node end){
    bool visited[10][10] = { false };  // 定义记录访问过节点的布尔型数组
    stack<Node> path;  // 定义保存路径的栈
    path.push(start);  // 将起点入栈
    visited[start.x][start.y] = true;  // 将起点标记为已访问

    while (!path.empty()){
        Node current = path.top();  // 取出栈顶节点
        if (current.x == end.x && current.y == end.y){  // 如果找到终点，就输出路径
            cout << "路径如下：" << endl;

            stack<Node> reversepath;  // 声明一个辅助栈，用来保存反转后的顺序
            while (!path.empty()){
                reversepath.push(path.top());
                path.pop();
            }

            while (!reversepath.empty()){  // 打印辅助栈中的内容
                Node node = reversepath.top();
                cout << "( " << node.x << " , " << node.y << " ) ";
                reversepath.pop();
            }
            cout << endl;
            return;
        }

        bool has_unvisited = false;  // 定义布尔型变量，标记是否还有未访问的节点
        for (int i = 0; i < 4; i++){  // 枚举上、右、下、左四个方向
            int next_x = current.x + directions[i][0];
            int next_y = current.y + directions[i][1];
            if (next_x >= 0 && next_x < 10 && next_y >= 0 && next_y < 10
              && maze[next_x][next_y] == 0 && !visited[next_x][next_y]){  // 判断是否是合法的下一个节点
                Node next_node = { next_x, next_y, path.size() };  // 创建下一个节点
                visited[next_x][next_y] = true;  // 标记下一个节点为已访问
                path.push(next_node);  // 将下一个节点入栈
                has_unvisited = true;  // 更新变量
                break;
            }
        }

        if (!has_unvisited){  // 如果没有未访问的节点，就弹出当前节点
            path.pop();
        }
    }

    cout << "未找到可行路径！" << endl;
}

int main(){
    Node start = { 0,0,-1 };  // 设置起点
    Node end = { 9,9,-1 };  // 设置终点
    DFS(start, end);  // 调用深度优先搜索函数
    system("pause");
    return 0;
}