前言

迪杰斯特拉(Dijkstra)算法是由荷兰计算机科学家狄克斯特拉于1959年提出的,因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法,解决的是有权图中单源最短路径问题。迪杰斯特拉算法主要特点是从起始点开始,采用贪心算法的策略,每次遍历到始点距离最近且未访问过的顶点的邻接节点,直到扩展到终点为止。
不太懂的可以看视频 QWQ (来着@Abel)
Dijkstra算法讲解
算法实现:
- 定义一个数组dist[],dist[i]表示从起点到顶点i的最短路径长度,初始化为无穷大,dist[s]=0,其中s为起点。
- 定义一个数组visited[],visited[i]表示顶点i是否已经被标记为已确定最短路径的顶点,初始化为false。
- 从dist[]中找到当前未被标记的dist[i]最小的顶点u,标记visited[u]=true。
- 遍历所有与u相邻的顶点v,如果visited[v]=false,且从起点到u再到v的路径长度小于dist[v],则更新dist[v]=dist[u]+w(u,v),其中w(u,v)为边(u,v)的权值。
重复步骤3和步骤4,直到所有顶点都被标记为已确定最短路径的顶点。

以下是求无向网(储存方式为邻接矩阵)中起点s到各点的最短路径的代码:
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <stdbool.h>
#include <malloc.h>
#define MVNum 100//最大顶点数
#define MaxInt 66666//表示极大值
typedef struct {
char vexs[MVNum];//顶点表(顶点为字符型)
int arcs[MVNum][MVNum];//邻接矩阵(权值为整型)
int vexnum, arcnum;//图的当前点数和边数
}AMGraph;
//定位
int LocateVex(AMGraph* G, char v) {
int i;
for (i = 0; i < G->vexnum; i++) {
if (G->vexs[i] == v) {
return i;
}
}
return -1;
}
//无向网的建立
AMGraph* CreateUDN() {
int i, j, k, w;
char v1, v2;
AMGraph* G = malloc(sizeof(AMGraph));
printf("输入总顶点数,边数\n");
scanf("%d%d", &G->vexnum, &G->arcnum);
getchar();//吸收换行符
printf("依次输入点的信息\n");
for (i = 0; i < G->vexnum; i++) {
scanf("%c", &G->vexs[i]);
}
getchar();//吸收换行符
for (i = 0; i < G->vexnum; i++)
for (j = 0; j < G->vexnum; j++) {
if (i == j) {
G->arcs[i][j] = 0;
}
else {
G->arcs[i][j] = MaxInt;
}
}
for (k = 0; k < G->arcnum; k++) {
printf("输入一条边依附的顶点及权值\n");
scanf("%c%c", &v1, &v2);
scanf("%d", &w);
getchar();//吸收换行符
i = LocateVex(G, v1), j = LocateVex(G, v2);//确定v1、v2在顶点数组的下标
G->arcs[i][j] = w;//边<v1,v2>权值置为w
G->arcs[j][i] = w;//无向网对称边<v2,v2>权值也置为w
}
return G;
}
//输出邻接矩阵
void print(AMGraph* G) {
int i, j;
printf(" ");
for (i = 0; i < G->vexnum; i++) {
printf("%c ", G->vexs[i]);
}
printf("\n");
for (i = 0; i < G->vexnum; i++) {
printf("%c ", G->vexs[i]);
for (j = 0; j < G->vexnum; j++) {
if (G->arcs[i][j] == MaxInt)
printf("∞ ");
else
printf("%d ", G->arcs[i][j]);
}
printf("\n");
}
}
//迪杰斯特拉算法
void Dijkstra(AMGraph* G, int s) {
int dist[MVNum];//用来储存各顶点与起点的距离
bool visited[MVNum];//用来标记已确定最短路径的顶点
int i, j, k, u, min;
//初始化数组dist与visited
for (i = 0; i < G->vexnum; i++) {
dist[i] = MaxInt;
visited[i] = false;
}
dist[s] = 0;//起始点s最短距离为0
//每次循环会标记一个顶点u,直到所有顶点被标记(循环次数就是顶点数-1,起点已找到最短路径0)
for (k = 1; k < G->vexnum; k++) {
min = MaxInt;
//找到当前未被标记的距离起点最近的顶点u
for (i = 0; i < G->vexnum; i++) {
if (dist[i] < min && !visited[i]) {
u = i;
min = dist[i];
}
}
visited[u] = true;//标记顶点u
/*遍历顶点u的邻结点,当 dist[u] + G->arcs[u][j] < dist[j]时
(顶点u距离起点s的长度dist[u]加上顶点u与邻接点j的距离G->arcs[u][j]小于顶点j距离起点s的距离dist[j]),
更新顶点j距离起点的路径长度*/
for (j = 0; j < G->vexnum; j++) {
if (!visited[j] && dist[u] + G->arcs[u][j] < dist[j]) {
dist[j] = dist[u] + G->arcs[u][j];
}
}
}
//输出结果
for (i = 0; i < G->vexnum; i++) {
printf("起点%c到顶点%c的最短路径为:%d\n", G->vexs[s], G->vexs[i], dist[i]);
}
}
int main() {
AMGraph* G = CreateUDN();
printf("该无向网邻接矩阵为:\n");
print(G);
Dijkstra(G, 0);
}若顶点数为n,求解最短路径的主循环共进行n-1次,每次执行的时间为,所以算法时间复杂度为。
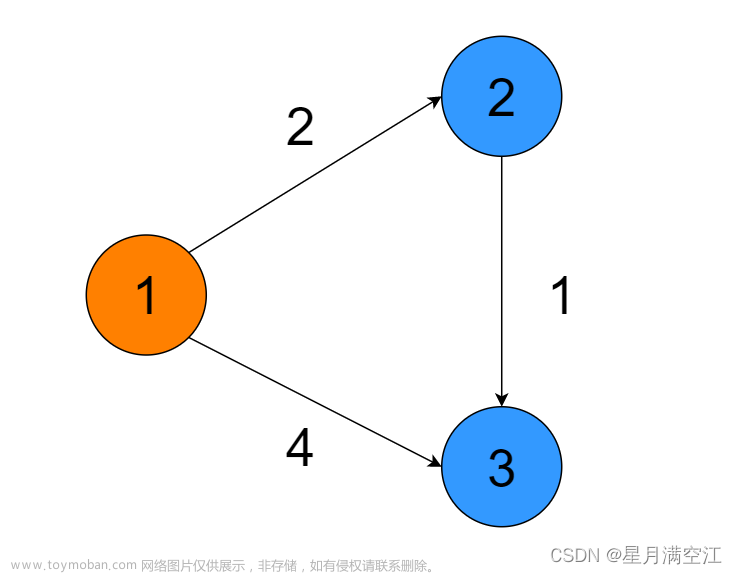
示例:
求如下图所示v0到各点的最短路径

运行结果如下:
A、B、C······代替v0、v1、v2······
 文章来源:https://www.toymoban.com/news/detail-770475.html
文章来源:https://www.toymoban.com/news/detail-770475.html
总结
如果是有向网或者是以邻接表方式储存的有权图,算法实现流程还是一样的,只不过代码上大同小异。文章来源地址https://www.toymoban.com/news/detail-770475.html
到了这里,关于C语言 最短路径 迪杰斯特拉(Dijkstra)算法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!