线性代数(应用篇)：Ch5.相似理论 Ch6.二次型

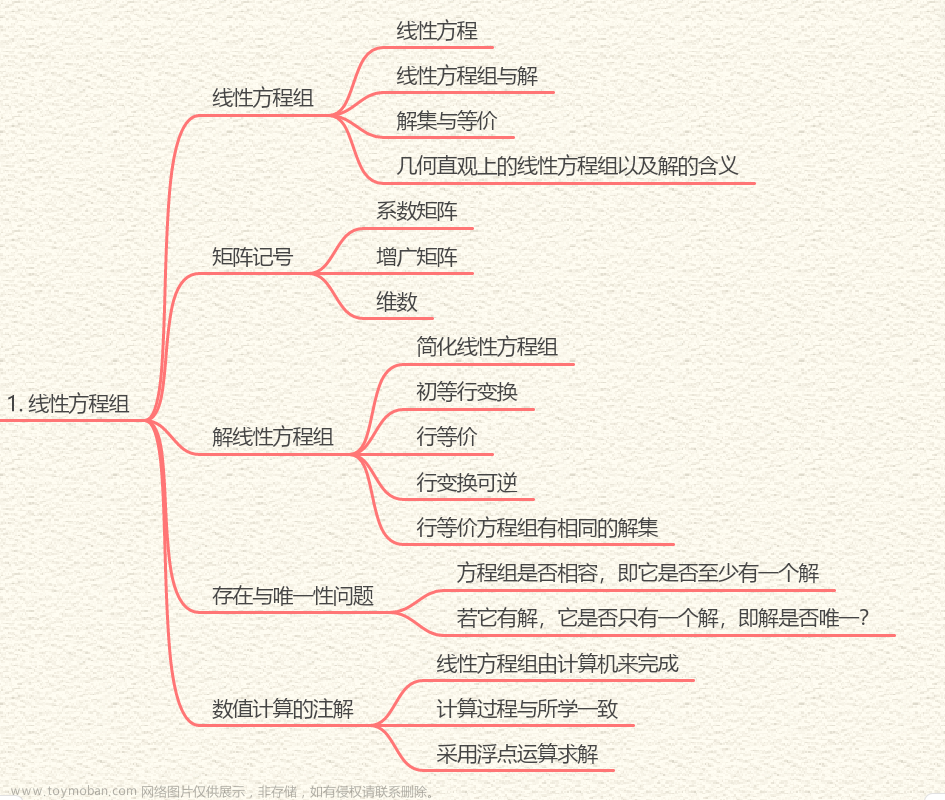
第5章 特征值与特征向量、相似矩阵

(一) 特征值与特征向量

1.定义

设$A$是$n$阶方阵，$\lambda$是一个数，若存在$n$维非零列向量$\xi$，使得$$A\xi =\lambda \xi (\xi \ne 0)$$则称$\lambda$是$A$的特征值，$\xi$是$A$的对应于(属于)特征值$\lambda$的特征向量。

注：
①只有方阵才有特征值和特征向量
②n阶方阵有n个特征值

$A_{n\times n}\times {\xi }_{n\times 1}=\lambda {\xi }_{n\times 1}$：即矩阵A作用在ξ上的效果，和一个数λ作用在ξ上的效果，是划等号的。即可用这个值来代表这个矩阵，即λ为矩阵的特征值。

其他概念：
①特征矩阵：λE-A
②特征多项式： $f(\lambda )=|\lambda E-A|$
③特征方程：f(λ)=|λE-A|=0

2.性质

1.特征值的性质

(1)特征值之和 = 主对角线元素之和：$\sum _{i=1}^n{\lambda }_i=\sum _{i=1}^n{a}_{ii}=tr(A)$
特征值之积 = 行列式 ：$\prod _{i=1}^n{\lambda }_i=|A|$

(2)上下三角矩阵、对角阵的主对角线元素，就是特征值

(3)若r(A)=1，则矩阵A的全部特征值为 tr(A),0,0,…,0

(4)设$f(x)$为多项式，若${\lambda }_1,{\lambda }_2,...,{\lambda }_n$为A的特征值，则$f({\lambda }_1),f({\lambda }_2),...,f({\lambda }_n)$为$f(A)$的特征值 【17年5.】

2.特征向量的性质

①k重特征值至多有k个线性无关的特征向量
②不同特征值对应的特征向量线性无关
③特征向量的线性组合，依然为特征向量 (只要求整体非零) (特征向量就是非零齐次解，齐次解的线性组合仍为齐次解)

3.求解

(1)具体型矩阵

1.求特征值：解$|\lambda E-A|=0$，求出n个${\lambda }_i$
2.求特征向量：
①将${\lambda }_i$代回齐次线性方程组 $({\lambda }_{i}E-A)x=0$，求出$(\lambda E-A)x=0$的基础解系 ${\xi }_1，{\xi }_2，...，{\xi }_n$
②矩阵A的属于特征值λ的全部特征向量为：齐次方程组$(\lambda E-A)x=0$的通解去掉零解，即$k_1{\xi }_1+k_2{\xi }_2+...+k_n{\xi }_n$ (k₁,k₂,…,k_n不全为0)

即，特征向量是$(\lambda E-A)x=0$的非零通解

三阶多项式分解因式：试根法、多项式带余除法

当该3阶矩阵的特征方程$|\lambda E-A|=0$ 不好求特征根时，可全部展开为3次多项式，使用试根法先求出一个根，得到 $(\lambda -{\lambda }_1)$，再用多项式带余除法，得到 $(\lambda -{\lambda }_2)(\lambda -{\lambda }_3)$

1.试根法
对于$f(\lambda )=a_k{\lambda }^k+...+a_3{\lambda }^3+a_2{\lambda }^2+a_1\lambda +a_0=0$
①若 $a_0=0$，则 $f(\lambda )=0$ 是根
②若 系数之和为0，则 $f(\lambda )=1$ 是根
③若 奇次方系数 = 偶次方系数，则 $f(\lambda )=-1$ 是根
④若 $a_k=1$，各系数均为整数，则 根均为整数，且 根均为 $a_0$的因子

2.多项式带余除法
缺项要补位

例题1：入门级别，求特征值和特征向量

答案：

例题2：真题，不太方便直接求出特征值，可考虑直接展开为3次多项式，用试根法+多项式带余除法

例题3：性质证明，不同特征值对应的特征向量线性无关

证明：

(2)抽象型矩阵：$f(A)$与$f(\lambda )$及特征向量的对应关系表格

$A^{\ast }$的特征值：${\lambda }^{\ast }=\frac{|A|}{\lambda }$

特征向量的性质：特征向量的非零线性组合，仍为特征向量。

①∴求特征向量时，求出基础解系是ξ后，要加k。最终的(全部的) 特征向量为kξ (k≠0)
②已知A的特征向量为ξ，则kA、A^-1、A*、A^k、f(A)的特征向量均为ξ
但仅有 kA、A^-1的特征向量为ξ时，也有A的特征向量为ξ

例题1：

分析：利用 ${\lambda }^{\ast }=\frac{|A|}{\lambda }$，求出$A^{\ast }$的特征值${\lambda }^{\ast }$

答案：11

例题2：23李林六套卷(六)15.   特征值的性质：主对角线元素之和 = 迹 = 特征值之和

分析：A*的主对角元素为A₁₁、A₂₂、A₃₃

答案：1

例题3：18年13.

分析：特征向量的线性组合也为特征向量

答案：-1

例题4：21年15.

分析：
法一：行列式的按行按列展开定理
法二：利用 ${\lambda }^{\ast }=\frac{|A|}{\lambda }$，求出$A^{\ast }$的特征值${\lambda }^{\ast }$

答案：$\frac{3}{2}$

(二) 相似

相似理论：①A~B ②A~Λ ③应用

1.矩阵相似

1.相似的定义

设A,B为n阶方阵，若存在可逆矩阵P，使得 P^-1AP = B，则称 矩阵A与B相似，或称A,B是相似矩阵，记为A~B 。称P为A到B的相似变换矩阵或过渡矩阵。

两矩阵相似：①定义法 ②传递法

2.相似的性质

(1)相似的必要条件

若$A\sim B$，则A、B的 特征多项式、特征值、秩、行列式、迹 相同。若可相似对角化，则相似于同一个对角阵。

①特征多项式相同：$|\lambda E-A|=|\lambda E-B|$
②特征值相同 (特征值相同+实对称矩阵 → 相似)
③秩相等 $r(A)=r(B)$ 、$r(\lambda E-A)=r(\lambda E-B)$
④行列式相等 $|A|=|B|={\lambda }_1\cdot {\lambda }_2\cdot {\lambda }_3$   且
⑤迹相等 $tr(A)=tr(B)={\lambda }_1+{\lambda }_2+{\lambda }_3$ l
⑥A~B，则A等价于B，即A可通过初等变换化为B

$A\sim B\Rightarrow \{\begin{array}{rl}(1)& |\lambda E-A|=|\lambda E-B|\\ (2)& A,B有相同的特征值\\ (3)& r(A)=r(B)\\ (4)& |A|=|B|=\prod _{i=1}^n{\lambda }_n\\ (5)& \sum _{i=1}^n{a}_{ii}=\sum _{i=1}^n{b}_{ii}=\sum _{i=1}^n{\lambda }_i，即tr(A)=tr(B)=tr(\Lambda )\end{array}$

(2)若 $A\sim B，则\{\begin{array}{rl}⇦⇨& A^{-1}\sim B^{-1}(可逆)\\ ⇦⇨& A^T\sim B^T\\ ⇨& A^{\ast }\sim B^{\ast }(可逆)\\ ⇨& f(A)\sim f(B)，A^m\sim B^m\\ ⇦⇨& A\sim C,B\sim C\end{array}$

A~B，若A可逆，则 AB~BA。
证明：∵A可逆 ∴A^-1(AB)A=BA ∴AB~BA

例题1：已知矩阵A、B。要求可逆矩阵P，使得$P^{-1}AP=B$。
分析：
我们没有学过直接相似的定理。都需要经过对角矩阵来实现传递性，即$A\sim \Lambda ，B\sim \Lambda$ ⇨ $A\sim B$。即有$P_1^{-1}A{P}_1=\Lambda ，P_2^{-1}B{P}_2=\Lambda$，$\therefore P_1^{-1}A{P}_1=P_2^{-1}B{P}_2$，$\therefore P_2{P}_1^{-1}A{P}_1{P}_2^{-1}=B$。即 存在$P=P_1{P}_2^{-1}$，使得$P^{-1}AP=B$

答案：$P=P_1{P}_2^{-1}$

例题1：P可逆，求AP=PB：P^-1AP=B
例题1变式：P不可逆，求AP =PB：解矩阵方程

例题2：880 相似矩阵 基础解答2(Ⅱ)

例题3：15年21.(1)、20年20.(1)

$\because A\sim B\therefore \{\begin{array}{c}tr(A)=tr(B)\\ |A|=|B|\end{array}$

例题2：16年05.

分析：需要掌握相似性质的证明
已知A~B，则若存在可逆矩阵P使得P^-1AP = B。此题额外附加了A、B均为可逆矩阵的条件
①证明：A^-1~B^-1
∵P^-1AP = B
对两边取逆
得 P^-1A^-1P = B^-1，即A^-1~B^-1

②证明：A^T~B^T
∵P^-1AP=B
对两边取转置
得 P^TA^T(P^-1)^T = B^T
即 [(P^T)^-1]^-1A^T(P^T)^-1 = B^T
令Q = (P^T)^-1 = (P^-1)^T，则 Q^-1A^TQ = B^T，则 A^T~B^T

③在此题A、B均为可逆矩阵的前提下，D正确
P^-1AP = B
P^-1A^-1P = B^-1
∴P^-1(A+A^-1)P = B+B^-1

④C，需要A、B均为实对称矩阵

答案：C

3.两矩阵是否相似的判别与证明

1.判断A B 相似：
①定义法：$P^{-1}AP=B$，则$A\sim B$
②传递法：$A\sim {\Lambda }_1,B\sim {\Lambda }_2，{\lambda }_A={\lambda }_B$，则${\Lambda }_1={\Lambda }_2$，即$A\sim \Lambda \sim B$

(1)两个实对称/可相似对角化的矩阵相似的充要条件

两实对称矩阵/两可相似对角化的矩阵 相似 ⇦⇨ 特征多项式相同 ⇦⇨ 特征值全部相同

对于普通矩阵来说，特征多项式相同、特征值相同，只是相似的必要条件。
但对于两个 实对称/可对角化 的矩阵 来说，特征多项式相同、特征值相同等相似的必要条件，就变成了相似的充分必要条件。

证明：
1.若A、B均可相似对角化，且A、B特征值相同，则A、B相似于同一个对角阵。则$P^{-1}AP=\Lambda ，A\sim \Lambda P^{-1}BP=\Lambda ，B\sim \Lambda$
由相似的传递性，可知$A\sim \Lambda \sim B，\therefore A\sim B$

2.若A、B均为实对称矩阵。实对称矩阵一定可以相似对角化，再接1的证明

条件由强到弱依次是：
①实对称
②不对称但可相似对角化
③不对称，也不可相似对角化

(2)非实对称矩阵相似

(1)充要条件：若两矩阵相似，则特征矩阵也相似，则特征矩阵的秩相等。即 $A\sim B⇦⇨kE-A\sim kE-B$
(2)必要条件：A~B → r(A)=r(B)
λE-A ~ λE-B → r(λE-A) = r(λE-B)

证明：

例题1：18年5.

分析：
显然，M、A、B、C、D的特征值均为1，1，1。$M\sim A⇦⇨kE-M\sim kE-A\to r(kE-M)=r(kE-A)$
r(E-M)=2，r(E-A)=2，r(E-B)=r(E-C)=r(E-D)=1，∴E-M~E-A

答案：A

例题2：13年06.   实对称矩阵相似的充要条件：特征值相同

分析：

答案：B

2.相似对角化

1.定义

A可相似于对角阵，称为A可相似对角化，即：
对于n阶矩阵A，存在n阶可逆矩阵P，使得 P − 1 A P = Λ = ( λ 1 λ 2 λ 3 ) P^{-1}AP=Λ=\left(\begin{array}{cc} λ₁ & & \\ & λ₂ & \\ & & λ₃\\ \end{array}\right) P−1AP=Λ= ​λ1​​λ2​​λ3​​ ​，其中$\Lambda$为对角阵，记作 $A\sim \Lambda$，称A可相似对角化。称$\Lambda$是A的相似标准形。P称为A到$\Lambda$的相似变换矩阵或过渡矩阵。

2.相似对角化的条件（n阶矩阵A可相似对角化的条件）

②$k_i=n-r({\lambda }_{i}E-A)$，${\lambda }_i$是$k_i$重根

注：
1.对于普通矩阵A：
①特征值不同 (${\lambda }_1\ne {\lambda }_2$)：特征向量 ${\xi }_1{\xi }_2$一定线性无关
②特征值相同 (${\lambda }_1={\lambda }_2$)：特征向量${\xi }_1{\xi }_2$ 可能无关，可能相关
2.A可相似对角化最本质的充要条件：A有n个线性无关的特征向量

3.相似对角化的性质

相似的两矩阵若均可相似对角化，则可以相似于同一个对角矩阵。该对角矩阵的主对角线元素即为特征值 λ₁、λ₂、λ₃

选择、填空：

例题1：17年6.   相似对角化的条件

分析：
A、B为上三角矩阵，C为对角矩阵。显然，A、B、C的特征值均为 2，2，1。
判断A、B是否与C相似， 即A、B能否相似对角化。
由相似对角化的充要条件：2重根,要有2个线性无关的特征向量，n-r(λE-A)=3-1=2 ∴r(λE-A)=1

显然，r(2E-A)=1，而r(2E-B)=2，∴A可以相似对角化，B不可以

答案：B

大题：

例题1：给定矩阵A，求可逆矩阵P，使得A可相似对角化，即$P^{-1}AP=\Lambda$

步骤：①求特征值与特征向量 ②令 $P=({\alpha }_1,{\alpha }_2,{\alpha }_3)$ ③②验证α₁,α₂,α₃线性无关，若无关则P可逆 ④P可逆，则有 P − 1 A P = Λ = ( λ 1 λ 2 λ 3 ) P^{-1}AP=Λ=\left(\begin{array}{cc} λ₁ & & \\ & λ₂ & \\ & & λ₃\\ \end{array}\right) P−1AP=Λ= ​λ1​​λ2​​λ3​​ ​

例题2：20年20.(2)   同19年21：两矩阵相似，且均可相似对角化

分析：
(1)①二次型与矩阵的对应关系 ②正交变换也是相似变换
(2) ∵二阶矩阵A、B均有2个互异的特征值，∴A、B均可相似对角化
且∵A~B，∴A、B相似于同一个对角矩阵

设A ~ Λ，则存在可逆矩阵P₁使得 $P_1^{-1}A{P}_1=\Lambda$
设B ~ Λ，则存在可逆矩阵P₂使得 $P_2^{-1}B{P}_2=\Lambda$
$\therefore B=P_2\Lambda P_2^{-1}=P_2{P}_1^{-1}A{P}_1{P}_2^{-1}$
令$P=P_1{P}_2^{-1}$，$\therefore B=P^{-1}AP$

所以，求出P₁、P₂，得$P=P_1{P}_2^{-1}$。对P进行正交化单位化，得正交矩阵Q

4.求可逆矩阵P，使得：①$P^{-1}AP=\Lambda$ ②$P^{-1}AP=B$

(1)求可逆矩阵P，使得$P^{-1}AP=\Lambda$

①求出A的全部特征值 λ₁ λ₂ λ₃
②求出A的特征值对应的特征向量 α₁ α₂ α₃
③存在可逆矩阵P=(α₁,α₂,α₃)，使得 P − 1 A P = ( λ 1 λ 2 λ 3 ) P^{-1}AP=\left(\begin{array}{cc} λ₁ & & \\ & λ₂ & \\ & & λ₃\\ \end{array}\right) P−1AP= ​λ1​​λ2​​λ3​​ ​

例题1：880 相似矩阵 基础解答1

答案：

例题2：15年21.(2)

求可逆矩阵P，使P^-1AP为对角矩阵：
只需求出其特征值，以及对应的n个线性无关的特征向量即可

分析：
①求特征值：A~B，∴A和B特征值相同。因为B的0更多，特征值更好求，所以用矩阵B来求特征值。
②求特征向量：分别将3个特征值λ代入λE-A，化简矩阵，得线性无关的特征向量

解题步骤：
①|λE-B|= |三阶行列式| =(λ-1)²(λ-5) ∴B的特征值为1，1，5
∵A~B ∴A的特征值也为1，1，5

②将λ=1代入(λE-A)x=0，即(E-A)x=0
E-A =()→()，得A的属于特征值λ=1的线性无关的特征向量为α₁=( )，α₂=( )

将λ=5代入(λE-A)x=0，即(5E-A)x=0
5E-A=()→()，得A的属于特征值λ=5的线性无关的特征向量为α₃=( )

令P=(α₁,α₂,α₃)，则P^-1AP = ʌ =()

答案：

(2)求可逆矩阵P，使得$P^{-1}AP=B$：(A与B相似，A、B均可相似对角化)

①求出A的全部特征值 λ₁ λ₂ λ₃
②求出A的特征值对应的特征向量 α₁ α₂ α₃
③存在可逆矩阵P₁=(α₁,α₂,α₃)，使得 P 1 − 1 A P 1 = Λ = ( λ 1 λ 2 λ 3 ) P_1^{-1}AP_1=Λ=\left(\begin{array}{cc} λ₁ & & \\ & λ₂ & \\ & & λ₃\\ \end{array}\right) P1−1​AP1​=Λ= ​λ1​​λ2​​λ3​​ ​

④∵A~B，∴B的特征值也为 λ₁ λ₂ λ₃
⑤求出B的特征值对应的特征向量 β₁ β₂ β₃

⑥存在可逆矩阵P₂=(β₁,β₂,β₃)，使得 P 2 − 1 B P 2 = Λ = ( λ 1 λ 2 λ 3 ) P_2^{-1}BP_2=Λ=\left(\begin{array}{cc} λ₁ & & \\ & λ₂ & \\ & & λ₃\\ \end{array}\right) P2−1​BP2​=Λ= ​λ1​​λ2​​λ3​​ ​

⑦∴$P_1^{-1}A{P}_1=P_2^{-1}B{P}_2$
∴$P_2{P}_1^{-1}A{P}_1{P}_2^{-1}=B$，即$(P_1{P}_2^{-1}{)}^{-1}A(P_1{P}_2^{-1})=B$
令$P=P_1{P}_2^{-1}$，则$P^{-1}AP=B$

例题1：19年21.(2)   A、B相似，且A、B均可相似对角化：以各自相似于对角阵为桥梁

分析：
$A\sim B$ ⇨ $A\sim \Lambda ，B\sim \Lambda$   ∴$A\sim \Lambda \sim B$

∴$P_1^{-1}A{P}_1=\Lambda ，P_2^{-1}B{P}_2=\Lambda$

∴$P_1^{-1}A{P}_1=P_2^{-1}B{P}_2$，即 $P_2{P}_1^{-1}A{P}_1{P}_2^{-1}=B$，即$(P_1{P}_2^{-1}{)}^{-1}A{P}_1{P}_2^{-1}=B$

令$P=P_1{P}_2^{-1}$，得$P^{-1}AP=B$

例题2：24李林四(一)21.

分析：
(Ⅰ)求c：$r(\lambda E-A)=r(\lambda E-B)$，取二重特征值

(Ⅲ) 通解X=k₁α₁+k₂α₂ (k₁,k₂为任意常数)

若求特征向量 ξ=k₁α₁+k₂α₂，则k₁,k₂不全为0

5.证明题：可逆与相似

例题1：20年21.

例题2：24李林六(一) 21.

3.实对称矩阵的相似对角化

1.实对称矩阵的性质

①实对称矩阵必能相似对角化
②实对称矩阵必有n个线性无关的特征向量
③实对称矩阵 不同特征值对应的特征向量一定正交

④实对称矩阵的特征值都是实数
⑤非零的幂零矩阵一定不能相似对角化

①对于任一n阶实对称矩阵A，必存在正交矩阵Q，使得 Q − 1 A Q = Q T A Q = Λ = ( λ 1 λ 2 . . . λ n ) Q^{-1}AQ=Q^TAQ=Λ=\left(\begin{array}{cc} λ₁ & & \\ & λ₂ & \\ & & ...\\ &&& λ_n \end{array}\right) Q−1AQ=QTAQ=Λ= ​λ1​​λ2​​...​λn​​ ​
其中${\lambda }_1,{\lambda }_2,...,{\lambda }_n$为A的n个实特征值，矩阵Q的列向量为A的依次对应于${\lambda }_1,{\lambda }_2,...,{\lambda }_n$的两两正交的单位特征向量

例题1：24李林六(五)21.   实对称矩阵：不同特征值对应的特征向量必正交

2.用正交矩阵Q将 实对称矩阵A 对角化的步骤

根据上述结论，总结出正交变换矩阵Q将实对称矩阵A对角化的步骤为：
(1)求出A的全部特征值${\lambda }_1,{\lambda }_2,...,{\lambda }_n$
(2)对每个特征值${\lambda }_i$，求出其特征向量
(3)将特征向量正交化，再单位化
(4)将这些单位向量作为列向量构成正交矩阵Q，从而有 Q − 1 A Q = Q T A Q = Λ = ( λ 1 λ 2 . . . λ n ) Q^{-1}AQ=Q^TAQ=Λ=\left(\begin{array}{cc} λ₁ & & \\ & λ₂ & \\ & & ...\\ &&& λ_n \end{array}\right) Q−1AQ=QTAQ=Λ= ​λ1​​λ2​​...​λn​​ ​

例题1：证明：实对称矩阵不同特征值对应的特征向量一定正交

例题2：23李林四(一)6.

分析：

答案：B

3.正交矩阵、正交变换

(1)正交矩阵Q

1.正交矩阵定义：$Q{Q}^T=Q^{T}Q=E$

两向量正交：内积为0

2.正交矩阵性质：(A,B均为n阶正交矩阵)
(1) $Q^{-1}=Q^T$
(2) Q的各行向量两两正交，各列向量两两正交
(3)$|Q|=\pm 1$
(4)$Q^{-1}、Q^T、QB$也是正交阵
(5)方阵Q是正交矩阵的充要条件：Q的列向量组或行向量组为标准正交向量组

3.求正交矩阵Q，使得${\mathrm{Q}}^{\mathrm{T}}\mathrm{AQ}$为对角矩阵 (A为实对称矩阵)：
①求A的特征值：即求A的特征方程|λE-A|=0的全部解
②求A的特征向量：对求得的每一个特征值，将其代入$(\lambda E-A)x=0$，求出每个特征值对应的特征向量
③特征向量正交化：施密特正交化
④特征向量单位化。然后组成正交矩阵Q

(2)正交变换

1.定义：
若Q为正交矩阵，则线性变换X=QY称为正交变换。正交变换属于相似变换，不改变矩阵的特征值。
对任一n阶实对称矩阵A，必存在正交矩阵Q 使得A可以相似对角化，即 Q − 1 A Q = Q T A Q = Λ = ( λ 1 λ 2 . . . λ n ) Q^{-1}AQ=Q^TAQ=Λ=\left(\begin{array}{cc} λ₁ & & \\ & λ₂ & \\ & & ...\\ &&& λ_n \end{array}\right) Q−1AQ=QTAQ=Λ= ​λ1​​λ2​​...​λn​​ ​

2.若二次型$f(x_1,x_2,x_3)$在正交变换X=PY下的标准型为 $2y_1^2+y_2^2-y_3^2$ ，即 P T A P = ( 2 1 − 1 ) P^TAP=\left(\begin{array}{cc} 2 & & \\ & 1 & \\ && -1 \end{array}\right) PTAP= ​2​1​−1​ ​

3.性质：
(1)正交变换保持向量的内积不变
(2)正交变换保持向量的长度不变
(3)正交变换保持向量的夹角不变

只会将图形在坐标系中旋转，而不会拉伸或压缩图形。【正交变换：只旋转，不拉压】

正交变换，既相似又合同

例题1：11年13.   正交变换不改变矩阵的特征值、行列式=特征值之积

分析：

答案：1

例题2：22年21.(2)   ①二次型的定义 ②求正交矩阵、正交变换法化二次型为标准型 ③配方法

答案：

例题3：20年20(2)

4.反求参数、反求矩阵A、$A^k$

$P^{-1}AP=\Lambda$，则有：
①$A=P\Lambda P^{-1}$
②$A^k=P{\Lambda }^k{P}^{-1}$
③$f(A)=Pf(A)P^{-1}$

例题1：

分析：
$f({\lambda }_1)=f(1)=-2，f({\lambda }_2)=f(2)=-2，f({\lambda }_3)=f(3)=-2$

B = f ( A ) = P f ( Λ ) P − 1 = P ( f ( λ 1 ) f ( λ 2 ) f ( λ 3 ) ) P − 1 = − 2 P E P − 1 = − 2 E B=f(A)=Pf(Λ)P^{-1}=P\left(\begin{array}{cc} f(λ₁) & & \\ & f(λ₂) & \\ & & f(λ₃)\\ \end{array}\right) P^{-1}=-2PEP^{-1}=-2E B=f(A)=Pf(Λ)P−1=P ​f(λ1​)​f(λ2​)​f(λ3​)​ ​P−1=−2PEP−1=−2E

答案：-2E

第6章 二次型

(一) 二次型的定义与矩阵表示

1.二次型定义

二次型的矩阵表达式：$f(x)=x^{T}Ax$
即 f ( x 1 , x 2 , x 3 ) = ( x 1 , x 2 , x 3 ) ( a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ) ( x 1 x 2 x 3 ) = a 11 x 1 2 + a 22 x 2 2 + a 33 x 3 2 + f(x_1,x_2,x_3)=(x_1,x_2,x_3)\left(\begin{array}{cc} a₁₁ & a₁₂ & a₁₃ \\ a₂₁ & a₂₂ & a₂₃ \\ a₃₁ & a₃₂ & a₃₃ \\ \end{array}\right) \left(\begin{array}{c} x_1 \\ x_2 \\ x_3 \end{array}\right)=a₁₁x₁^2+ a₂₂x₂^2+a₃₃x_3^2+ f(x1​,x2​,x3​)=(x1​,x2​,x3​) ​a11​a21​a31​​a12​a22​a32​​a13​a23​a33​​ ​ ​x1​x2​x3​​ ​=a11​x12​+a22​x22​+a33​x32​+ $(a_{12}+a_{21})x_1{x}_2+(a_{13}+a_{31})x_1{x}_3+(a_{23}+a_{32})x_2{x}_3$

A为实对称矩阵 ($A=A^T$)，称为二次型的系数矩阵。

平方项：$x_i^2$、交叉项(混合项)：$x_i{x}_j、x_j{x}_i$

2.二次型的矩阵表示：二次型与矩阵的对应关系

1.看到二次型能写出矩阵，看到矩阵能写出它的二次型。
2.二次型f的矩阵，就是A，不能带x。二次型的定义是$f(x)=x^{T}Ax$

例题1：02年4.

分析：对二次型进行正交变换得标准形，实际上就是对矩阵进行相似对角化。正交变换得到的标准形对应矩阵都是对角矩阵，标准形系数都是特征值。

答案：2

例题2：23李林六套卷(五)15.   二次型定义、合同的定义及性质

答案：

3.二次型与二次曲面

二次型与二次曲面：直接求特征值，根据特征值正负判断曲面类型

f(x,y,z)=1：
①两正一负：单叶双曲面
②一正两负：双叶双曲面
③三正：椭球面
④两正一零：圆柱面

f(x,y,z)=0：
①两正一负/一正两负：圆锥面

例题1：24李林四(四)7.

分析：注意右边 = 0

答案：D

例题2：16年06.  二次型与二次曲面

分析：求特征值，看正负惯性指数，判断曲面类型

答案：B

例题3：880 二次型 基础选择6

分析：
解得特征值为-3，3，3。两正一负，为单叶双曲面。

答案：C

例题4：880 二次型 综合选择3

分析：
解得特征值为0，3，3。两正一零，为椭圆柱面。

答案：D

例题5：880 二次型 基础选择7

分析：椭球面，则特征值全正，对应正定二次型。Δ₁>0,Δ₂>0,Δ₃=|A|>0，取交集得k>0

答案：A

(二) 化二次型为标准型、规范型

1.线性变换

(1)可逆线性变换 x=Py

可逆线性变换：①正交变换 ②配方法

(2)正交变换 x=Qy

(3)合同变换：用于解决二次型问题

二次型的矩阵表示总是对称的。任何对称矩阵必可合同于对角矩阵。(实对称矩阵一定可相似对角化，即一定相似于对角矩阵，则一定可合同于对角矩阵)

例题1：23年21.

2.合同

(1)定义

设A,B为n阶方阵。若存在可逆矩阵P，使得 $P^{T}AP=B$，则称 矩阵A与B合同。记作$A\simeq B$。
此时称对应的二次型f(x)与g(y)为合同二次型。

(2)性质

1.两实对称矩阵A、B合同：
⇦⇨ A、B 正、负惯性指数 相同 【两合同矩阵的正负特征值个数相同】
⇦⇨ A、B 正惯性指数相同 + 秩相同
⇦⇨ p、q、r均相同

(3)相似与合同

1.相似的必要条件：(用于排除)
①特征值相同 ⇨ 行列式相等、迹相等。若A B为实对称矩阵，则为充要条件。
②秩相同：$r(A)=r(B)$、$r(\lambda E-A)=r(\lambda E-B)$

2.合同：
①若A,B合同，则A,B要么都为实对称，要么都不对称。若A,B中一个为实对称，一个不为实对称，则A,B不合同。
②合同的必要条件：正负惯性指数相同。若A B为实对称矩阵，则为充要条件。
③实对称矩阵，若相似，一定合同

对称矩阵和不对称矩阵，不可能合同
证明：设A与B合同，A=A^T，B≠B^T。
存在可逆矩阵P，使得 P^TAP=B①。两边取转置得，P^TA^TP=B^T
∵A=A^T，得P^TAP=B^T②
∵B≠B^T ∴①与②矛盾。故对称矩阵与不对称矩阵不合同。

例题1：24李林六(二)7.

分析：
A.A与C均为三角阵，特征值不同，不符合相似的必要条件。A❌
B.A不为实对称矩阵，B为实对称矩阵，A B不合同。B❌
C.D. B与C均为实对称矩阵，则实对称矩阵相似必然合同。若能选D，一定能选C。故只能选C

答案：C

例题2：07年8. 相似与合同：实对称矩阵

分析：
①A与B均为实对称矩阵，若相似 必合同，排除C
②由|λE-A|=0求得A的特征值为3,3,0。对角阵B的特征值为1,1,0。A,B不相似，排除A。
③实对称 + 正惯性指数和秩相同，因此A B合同。

答案：B

例题3：01年9.

分析：
A、B均为实对称矩阵，若相似，必合同
A的秩为1，故A的特征值为 λ₁=tr(A)=4,其余为0。对角阵B的特征值也为λ₁=4,λ₂=λ₃=λ₄=0
实对称矩阵，特征值相等 是 相似的充要条件。选A

答案：A

例题4：880 相似矩阵 综合选择3

分析：
①与对称阵合同的一定是对称阵，排除A
②由相似的必要条件，迹相同。只有C符合，排除BD

答案：C

3.标准形、规范形

(1)标准形

1.标准形：与对角矩阵对应的二次型$f$只含有变量的平方项，没有变量的交叉乘积项，即为标准形。
2.由正交矩阵Q通过正交变换x=Qy得到的标准形，其平方项系数为$f$对应的矩阵A的特征值

(2)规范形

1.规范形：只含有平方项，且平方项的系数仅为 1，-1，0

①为什么要化为“标准形”、“规范形”？
答：标准形、规范形只含平方项，二次型对应的二次曲面方便找出最大值。
②如何化为标准形、规范形？
对A做相似对角化，化为相似的对角阵，主对角线元素均为特征值。满足只含平方项。

例题1：18年20(2)   线性方程组、规范形

分析：
(1)平方和为0，则每个括号内都为0

(3)正交变换法 化二次型为标准形：得对角阵，系数为特征值

1.定理
任意给定实二次型 $f=x^{T}Ax(A^T=A)$，一定存在正交变换 $x=Qy$，使$f$化为标准形 $f={\lambda }_1{y}_1^2+{\lambda }_2{y}_2^2+...+{\lambda }_n{y}_n^2$ 。其中${\lambda }_i(i=1,2,...,n)$为二次型矩阵A的特征值。

2.性质
①正交变换相当于对实对称矩阵A做了相似对角化，得到的平方项系数即为A的特征值。【而配方法得到的系数一般不是特征值。】
②正交变换法只能化二次型为标准形，不能化为规范形（除非特征值都属于{1,-1,0}）

3.用正交变换化二次型为标准形的步骤：
(1)写出二次型对应的实对称矩阵A
(2)求出A的所有特征值λ₁ λ₂ λ₃ 和 特征向量ξ₁ ξ₂ ξ₃
(3)将特征向量正交化得β₁ β₂ β₃，单位化 得 β₁^o β₂^o β₃^o，得正交矩阵 Q = ( β 1 o β 2 o β 3 o ) = ( λ 1 λ 2 λ 3 ) Q=(β₁^o β₂^o β₃^o)=\left(\begin{array}{cc} λ₁ & & \\ & λ₂ & \\ & & λ₃\\ \end{array}\right) Q=(β1o​β2o​β3o​)= ​λ1​​λ2​​λ3​​ ​
即正交变换 x=Qy 将二次型f化为标准形 ${\lambda }_1{y}_1^2+{\lambda }_2{y}_2^2+{\lambda }_3{y}_3^2$

例题1：15年6.

分析：

答案：A

例题2：12年21.

分析：秩的性质、正交变换的步骤

答案：(1)a = -1

①求$f(x_1,x_2,x_3)=0$ 的解

利用平方项的和为0，转化为线性方程组

例题1：18年20.(1)

例题2：22年21(3)

(4)配方法 化二次型为标准形、规范形

配方法：
①将某个$x_i$的平方项及与其有关的所有混合项，一次性配成一个完全平方。如此，直到全部配成完全平方项。
②n元要n换，缺项要补项(+0倍$x_3$，令$y_3=x_3$)，得到$Y=C^{-1}X$
③反解出C，即 X=CY

若要化二次型为规范形，只可使用配方法。正交变换法只能化到标准形，正交变换化的标准形的系数是实对称矩阵A的特征值。

例题1：880 二次型 基础解答1(Ⅱ)   配方法

分析：
(Ⅱ)一次解决一个自变量

答案：

例题2：14年13.   配方法求二次型的标准形

分析：初等变换改变特征值，相似变换不改变特征值

答案：[-2,2]

例题3：没有平方项，创造平方项

分析：化为规范形，只能使用配方法

答案：

(三) 正定二次型

1.惯性定理

惯性定理：可逆线性变换，不改变正负惯性指数

①正惯性指数p：正特征值的个数
②负惯性指数q：负特征值的个数。满秩时，负惯性指数为奇数，行列式<0
③$r=p+q$

例题1：14年13.   正负惯性指数

分析：
求特征值时，不可进行初等变换(初等变换会改变特征值)，不要化为行最简。此题直接求特征值困难。
满秩时，负惯性指数为奇数，行列式<0

答案：[-2,2]

2.正定二次型、正定矩阵、 二次型正定性的判别

(1)正定的定义

设 $f=x^{T}Ax(A^T=A)$为实二次型，若对于任意非零向量$x(x\ne 0)$，
(1)恒有 $f=x^{T}Ax>0$，则称 f=x^TAx 为正定二次型，称矩阵A为正定矩阵；
【即，当且仅当 $x=0$ 时，才有$f=x^{T}Ax=0$。当 $x\ne 0$ 时都有$f=x^{T}Ax>0$，则$f$为正定二次型】
恒有 $f=x^{T}Ax<0$，则称$f=x^{T}Ax$ 为负定二次型，称矩阵A为负定矩阵；

(2)恒有 $f=x^{T}Ax\ge 0$，则称 $f=x^{T}Ax$为 半正定二次型，称矩阵A为半正定矩阵；
恒有 $f=x^{T}Ax\le 0$，则称 $f=x^{T}Ax$为 半负定二次型，称矩阵A为半负定矩阵；

(3)若$f=x^{T}Ax$的值时而为正，时而为负，则称 $f=x^{T}Ax$ 为不定二次型

(2)正定的性质(充要条件)

矩阵A正定 (抽象型矩阵：先说A是实对称，$A^T=A$，再用充要条件)
⇦⇨ ①A的各阶顺序主子式 ${\Delta }_i>0$ (从左上角或右下角开始都可) 【具体型矩阵】
⇦⇨ ②A的所有特征值均为正值 ${\lambda }_i>0$ 【具体型、抽象型】
⇦⇨ ③A的正惯性指数 $p=r=n$ 【配方法求】
⇦⇨ ④对任意n维非零列向量 $x$，总有 $f=x^{T}Ax>0$ (正定的定义)
⇦⇨ ⑤A与单位阵E合同，即 $P^{T}AP=E$
⇦⇨ ⑥存在可逆矩阵Q，使得 $A=Q^{T}Q$
 ⇨ ⑦方程组仅有零解 ⇦⇨ |A|≠0

例题1：880 二次型 基础填空1

分析：各阶顺序主子式>0，取交集

答案：$-2<a<1$

例题2：880 二次型 综合填空2

分析：
$r(A_{m\times n})=n$，则矩阵$A^{T}A$正定

答案：n

例题3：设$r(A_{m\times n})=n$，证明：矩阵$A^{T}A$正定

答案：
对任意x≠0，有X^TA^TAX=(AX)^TAX>0，则矩阵A^TA正定

文章来源地址https://www.toymoban.com/news/detail-770714.html

到了这里，关于线性代数(应用篇)：Ch5.相似理论 Ch6.二次型的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！