一分钟读懂：矩阵的特征值分解、奇异值分解和伪逆矩阵

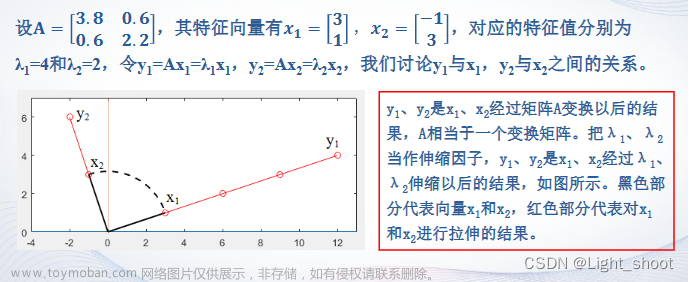
通过把矩阵运算分解成多个矩阵的乘法，可以简化矩阵运算，也可发现对应线性变换的一些内在规律和特性。根据不同的目的，有不同的分解策略。本文我们讨论最常用的特征值分解和奇异值分解。

1. 矩阵的乘方运算

定义了矩阵的加、减、乘、除（逆）运算后，数学家们自然希望探索矩阵更多的计算技巧。其中，矩阵的乘方运算 $A^n$ （$A$ 是方阵）成为一个引人注目的目标。例如，在离散系统动力学这类应用中，需要经常研究下述计算：
$${\mathbf{x}}_n=A{\mathbf{x}}_{n-1}=A^n{\mathbf{x}}_0$$

2. 特征值分解

矩阵的特征值分解可以解决矩阵的乘方问题，最关键的公式如下：
$$A=PD{P}^{-1}$$
有了特征值分解，矩阵乘方的计算可以大大简化，参见下面公式：
$$A^n=(PD{P}^{-1}{)}^n=P{D}^n{P}^{-1}$$
特征值矩阵 $D$ 是对角矩阵，乘方运算特别简单：
D n = [ λ 1 n . . . λ m n ] D^n=\left[ \begin{matrix} \lambda_1^n&&\\ &...&\\ &&\lambda_m^n \end{matrix} \right] Dn= ​λ1n​​...​λmn​​ ​
于是，矩阵乘方问题得以解决。

3. 伪逆矩阵

满秩方阵是可以求逆的。奇异矩阵（不满秩方阵）和非方阵能否实现逆运算？具体一点，如果
$$\mathbf{y}=A\mathbf{x}$$
是否存在矩阵 $A^{+}$，使得
$$\mathbf{x}=A^{+}\mathbf{y}$$
这里，$A^{+}$ 称为伪逆矩阵。

4. 对称矩阵

$A$ 可能不是方阵，但 $A{A}^T$ 或 $A^{T}A$ 都是方阵，而且还是对称矩阵。通过对矩阵 $A{A}^T$ 或 $A^{T}A$ 做特征值分解，可巧妙地解决伪逆矩阵的求法问题。不过先不要着急，我们介绍对称矩阵一个很重要的性质：对称矩阵的特征向量是相互正交的。 这一结论证明如下：

假设 $A^T=A$，其特征值 ${\lambda }_1,{\lambda }_2$ 对应的特征向量为 ${\mathbf{x}}_1,{\mathbf{x}}_2$，于是：
$$\begin{array}{lll}{\lambda }_1{\mathbf{x}}_1\cdot {\mathbf{x}}_2& =& ({\lambda }_1{\mathbf{x}}_1{)}^T{\mathbf{x}}_2\\ & =& (A{\mathbf{x}}_1{)}^T{\mathbf{x}}_2\\ & =& {\mathbf{x}}_1^T{A}^T{\mathbf{x}}_2\\ & =& {\mathbf{x}}_1^{T}A{\mathbf{x}}_2\\ & =& {\mathbf{x}}_1^T{\lambda }_2{\mathbf{x}}_2\\ & =& {\lambda }_2{\mathbf{x}}_1^T{\mathbf{x}}_2\\ & =& {\lambda }_2{\mathbf{x}}_1\cdot {\mathbf{x}}_2\end{array}$$
由于 ${\lambda }_1\ne {\lambda }_2$，于是，
$${\mathbf{x}}_1\cdot {\mathbf{x}}_2=0$$

5. 正交矩阵

因此，矩阵 $A{A}^T$ 或 $A^{T}A$ 的特征向量矩阵是正交矩阵。关于正交矩阵，有如下重要性质：

假设 $P$ 是正交矩阵，则：
$$P{P}^T=I$$
于是，得到
$$P^{-1}=P^T$$

6. A A T AA^T AAT 的特征值分解

接下来有好戏看了，我们来分解一下 $A{A}^T$：
$$A{A}^T=PD{P}^{-1}=PD{P}^T$$
其中，$D$ 是特征值矩阵，也是一个对角矩阵，$P$ 则是一个正交矩阵。上面的这个公式在强烈地提醒我们，矩阵 $A$ 大概可以分解成下面的形式：
$$A=PSQ$$
其中 $S$ 是对角矩阵，$P$ 是 $m\times m$ 正交矩阵，$Q$ 是 $n\times n$ 正交矩阵。如果真的如此的话，下面的公式应该成立：
$$A{A}^T=(PSQ)(PSQ{)}^T=PSQ{Q}^T{S}^T{P}^T=P{S}^2{P}^T$$
豁然开朗，原来对角矩阵 $S$ 是特征值矩阵 $D$ 的平方根，对角线上的这些非零数值就是所谓的奇异值。$S$ 和 $P$ 求出来后，$Q$ 可以如下求解：
$$\begin{gathered} A=PSQ \\ Q=S^{-1}{P}^{T}A=S^{-1}{P}^{T}A \end{gathered}$$
另外，$Q$ 是正交矩阵，原因如下：
$$\begin{array}{lll}Q{Q}^T& =& (S^{-1}{P}^{T}A)(S^{-1}{P}^{T}A{)}^T\\ & =& S^{-1}{P}^{T}A{A}^{T}P{S}^{-1}\\ & =& S^{-1}{P}^{T}PD{P}^{T}P{S}^{-1}\\ & =& S^{-1}D{S}^{-1}\\ & =& S^{-1}SS{S}^{-1}\\ & =& I\end{array}$$
于是，我们得到一般性的结论，奇异值分解对任何矩阵都有效，甚至适用于非方阵。

7. 奇异值分解

根据前面的分析，假设矩阵 $A$ 是 $m\times n(m\ne n)$，我们可以将矩阵 $A$ 分解如下。
$$A=U\Sigma V^T$$

• $U$是一个正交矩阵 $(m\times m)$
• $\Sigma$ 是一个对角线矩阵 $(m\times n)$
• $V$ 是一个正交矩阵 $(n\times n)$。

这就是矩阵的奇异值分解。矩阵 $A$ 的奇异值实际上就是 $A{A}^T$ 的特征值的平方根。

8. 求伪逆矩阵

有了前面的基础，终于可以求伪逆矩阵了。定义矩阵 $A$ 的伪逆矩阵 $A^{+}$ 如下：
$$\begin{gathered} A=U\Sigma V^T \\ {A}^{+}=V{D}^{+}{U}^T \end{gathered}$$

假设 $\Sigma$ 的定义如下：

Σ = [ σ 1 σ 2 . . . σ s 0 . . . 0 ] \Sigma= \left[ \begin{matrix} \sigma_1&&&&&&\\ &\sigma_2&&&&&\\ &&...&&&&&\\ &&&\sigma_s&&&\\ &&&&0&&&\\ &&&&&...&\\ &&&&&&0 \end{matrix} \right] Σ= ​σ1​​σ2​​...​σs​​0​...​0​​ ​

那么D+的定义如下：
D + = [ 1 σ 1 1 σ 2 . . . 1 σ s 0 . . . 0 ] D^+= \left[ \begin{matrix} \frac1{\sigma_1}&&&&&&\\ &\frac1{\sigma_2}&&&&&\\ &&...&&&&&\\ &&&\frac1{\sigma_s}&&&\\ &&&&0&&&\\ &&&&&...&\\ &&&&&&0 \end{matrix} \right] D+= ​σ1​1​​σ2​1​​...​σs​1​​0​...​0​​ ​
我们计算 $A^{+}A$ ：

$$\begin{array}{cclc}{A}^{+}A& =& (V{D}^{+}{U}^T)(U\Sigma V^T)& \\ & =& VD\Sigma V^T& Note:D^{+}\Sigma =I\\ & =& V{V}^T& \\ & =& I& \end{array}$$

以同样的方式，$A{A}^{+}=I$。
综上所述，如果我们能够对矩阵 $A$ 进行奇异值分解，我们就可以通过 $V{D}^{+}{U}^T$ 来计算 $A^{+}$，这是一个 $A$ 的伪逆矩阵。文章来源地址https://www.toymoban.com/news/detail-770832.html

到了这里，关于一分钟读懂：矩阵的特征值分解、奇异值分解和伪逆矩阵的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！