目录
前言
一、笛卡尔坐标系(Cartesian Coordinate System)
1.二维笛卡尔坐标系
2.三维笛卡尔坐标系
2.1.左手坐标系(left-handed coordinate space)
判断左手坐标系的方法:
判断左手坐标系的正向旋转(左手法则【left-hand rule】)
2.2.右手坐标系(right-handed coordinate space)
判断右手坐标系的方法:
判断右手坐标系的正向旋转(右手法则【right-hand rule】)
问题:为什么三维笛卡尔坐标系要区分左手坐标系和右手坐标系呢?
2.3Unity使用的坐标系
二、点和矢量
1、点(point)
2、矢量(vector)
3、矢量的运算
3.1.矢量的加减
3.2.矢量和标量的乘除
3.3.矢量的模、单位矢量和归一化
3.3.1.矢量的模:
3.3.2.矢量的单位矢量:
3.3.3.矢量的归一化(normalization):
3.3.4.为什么要归一化?
3.3.5.零矢量
3.4.矢量和矢量的乘法
3.4.1.点积(Dot product)
3.4.2.叉积(Cross product)
3.4.3.叉积的模
三、矩阵
1.什么是矩阵
2.矩阵的运算
2.1.矩阵和矩阵的加减
2.2.矩阵和标量的乘法
2.3.矩阵和矩阵的乘法
3.特殊矩阵
3.1.方块矩阵
3.2.对角元素
3.3.对角矩阵
3.4.单位矩阵
3.5.转置矩阵
3.6.逆矩阵
3.7.正交矩阵
4.矩阵的几何意义:变换
4.1.什么是变换
4.2.变换类型
4.2.1.线性变换
4.2.2.仿射变换
齐次坐标
4.3.分解基础变换矩阵
4.4.平移矩阵
4.5.缩放矩阵
4.6.旋转矩阵
4.7.复合变换
四、坐标空间
1、坐标空间的变换
2、模型空间(model space)
3、世界空间(world space)
4、观察空间(view space)
5、裁剪空间(clip space)
6、屏幕空间(screen space)
7、顶点的坐标空间变换过程
8、空间转换顺序
9、法线变换
五、Unity Shader的内置变量(数学)
前言
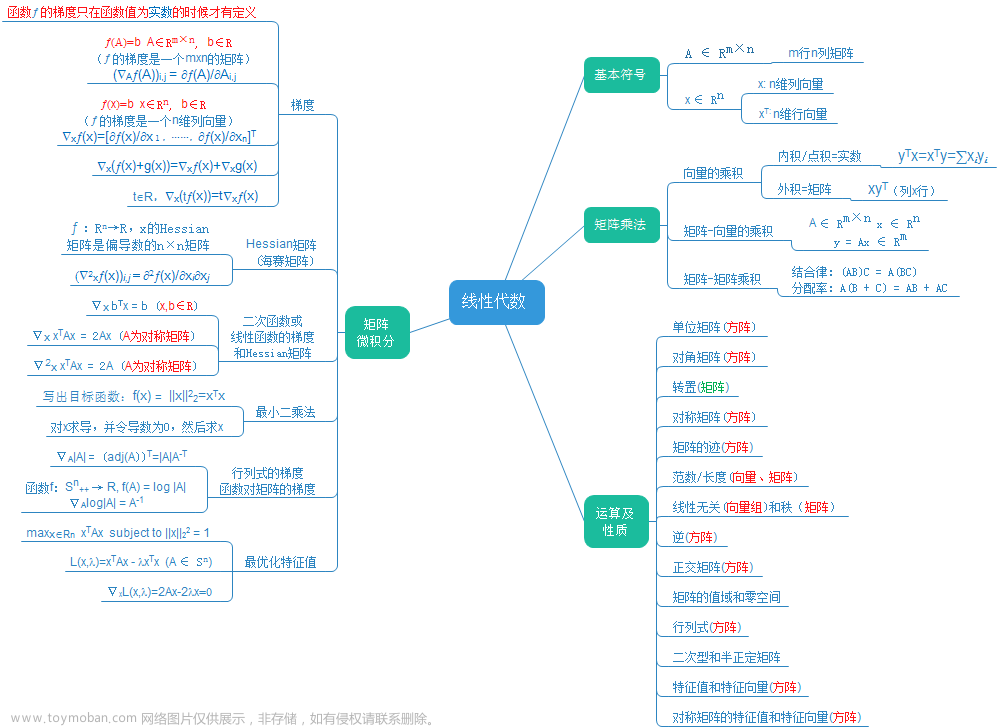
在学习Shader过程中,我们最常使用的就是矢量和矩阵(即数学的分支之一——线性代数)
一、笛卡尔坐标系(Cartesian Coordinate System)
笛卡尔坐标系的名字来源于法国伟大的哲学家、物理学家、心理学家、数学家笛卡尔。
1.二维笛卡尔坐标系
事实上,在现实中我们一直在使用二维笛卡尔坐标系,一个二维的笛卡尔坐标系包含了两部分的信息:
1)一个特殊的位置:原点,它是整个坐标系的中心
2)两条过原点的相互垂直的矢量,即x轴和y轴,这些坐标轴也被称为该坐标系的基矢量(basis vector)。
2.三维笛卡尔坐标系
在三维笛卡尔坐标系中,我们需要定义三个坐标轴和一个原点,这三个坐标轴也称为坐标系的基矢量。
通常情况下,这三个轴之间是互相垂直,且长度为1,这样的基矢量被称为标准正交基(orthonormal basis),但并不是必须的。
如果坐标轴互相垂直但长度不全为1,这样的基矢量被称为正交基(orthogonal basis)。
2.1.左手坐标系(left-handed coordinate space)
判断左手坐标系的方法:
法一:举起左手,食指和大拇指摆出一个"L"的手势,并且食指指向朝上,大拇指指向朝右,伸出中指,不出意外的话它的指向应该是你的前方
法二:身体坐直,向右伸直右手,此时右手的方向就是X轴的正向,而你的头顶就是Y轴的正向,如果你的正前方使Z轴的正向,那么你本身处于一个左手坐标系之中
判断左手坐标系的正向旋转(左手法则【left-hand rule】)
举起左手并握拳,伸出大拇指让它指向旋转轴的正方向,那么旋转的正方向就是剩下四个手指弯曲的方向
在左手坐标系中,旋转正方向是顺时针的
2.2.右手坐标系(right-handed coordinate space)
判断右手坐标系的方法:
法一:举起右手,食指和大拇指摆出一个"L"的手势,并且食指指向朝上,大拇指指向朝左,伸出中指,不出意外的话它的指向应该是你的前方
法二:身体坐直,向右伸直右手,此时右手的方向就是X轴的正向,而你的头顶就是Y轴的正向,如果你的正前方使Z轴的负向,那么你本身处于一个右手坐标系之中
判断右手坐标系的正向旋转(右手法则【right-hand rule】)
举起右手并握拳,伸出大拇指让它指向旋转轴的正方向,那么旋转的正方向就是剩下四个手指弯曲的方向
在右手坐标系中,旋转正方向是逆时针的
左右坐标系之间是可以相互转换的。最简单的方法就是把其中一个轴反转,并保持其它轴不变。
问题:为什么三维笛卡尔坐标系要区分左手坐标系和右手坐标系呢?
因为在二维笛卡尔坐标系下,x轴和y轴指向虽然可能不同,但总是可以通过一些旋转操作来使它们的坐标轴朝向相同,在某种意义上来说,所有二维笛卡尔坐标系都是等价的。
但是在三维笛卡尔坐标系中,靠旋转有时候并不能使两个不同朝向的坐标系重合。也就是说,三维笛卡尔坐标系并不是等价的。如果两个坐标系具有相同的旋向性(handedness),那么就可以用旋转的方法来让它们的坐标轴指向重合。如果不是,那么就无法达到重合的目的(比如左手坐标系和右手坐标系)
2.3Unity使用的坐标系
对于模型空间和世界空间,Unity使用的是左手坐标系,对于观察空间(通俗来讲就是以摄像机为原点的坐标系,在这个坐标系,摄像机的前向是z轴的负方向),Unity使用的是右手坐标系。
二、点和矢量
1、点(point)
点是n维空间中的一个位置,它没有大小、宽度这类概念。
2、矢量(vector)
矢量存在的意义更多是为了和标量(scalar)区分开,也称为向量,矢量是n维空间中包含了模(magnitude)和方向(direction)的有向线段。
矢量的模指代这个矢量的长度,矢量的方向则描述这个矢量在空间的指向。
一个矢量通常由一个箭头表示,矢量的头值它的箭头的端点处,尾指另一个端点处。
通常,矢量被用于表示相对于某个点的偏移(displacement),也就是说它是一个相对的量。只要矢量的模和方向保持不变,无论放在哪里都是同一个矢量。
3、矢量的运算
3.1.矢量的加减
矢量的加减法遵循三角形定则
矢量的加法:a+b=(ax+bx,ay+by,az+bz)
矢量的减法:a-b=(ax-bx,ay-by,az-bz)
3.2.矢量和标量的乘除
即是矢量的每一个分量乘或者除以标量,可以乘除负数,则方向相反
矢量和标量的乘法:ab=(bax,bay,baz)
矢量和标量的除法:a/b=(ax/b,ay/b,az/b)
3.3.矢量的模、单位矢量和归一化
3.3.1.矢量的模:
矢量的模是一个标量,是矢量在空间的长度
二维矢量的模:a²+b²=c²
三维矢量的模:
3.3.2.矢量的单位矢量:
单位矢量就是归一化后模为1的矢量
二维空间:半径为1的单位圆,单位矢量从圆心出发,到圆边界的矢量

三维空间:单位矢量就是从一个半径为1的球心出发、到达球面的矢量

3.3.3.矢量的归一化(normalization):
把非零矢量转换为单位矢量的过程就是归一化(矢量)
矢量除以矢量的模
3.3.4.为什么要归一化?
归一化其实就是数据缩放,一种线性变换。为了数据处理方便,也能加快程序的运行。 在计算光照模型的时候我们往往关心的只是矢量的方向而不是模。
3.3.5.零矢量
即矢量的每个分量值都是0,是不可以被归一化的,这是因为做除法运算时分母不能为0
3.4.矢量和矢量的乘法
3.4.1.点积(Dot product)
又称内积,结果是一个标量,可能是负数也可能是零,经常用于计算光照模型,即对应分量相乘再求和。点积的几何意义很重要,其中一个几何意义就是投影
a.b=axbx+ayby+azbz
当两个矢量方向相同(即夹角<90°)时,点积大于0。
当两个矢量方向垂直(即夹角=90°)时,点积等于0。
当两个矢量方向相反(即夹角》90°)时,点积小于0。
两个矢量的点积也可以用模相乘乘以夹角的余弦,即:a.b=|a||b|cos夹角。
3.4.2.叉积(Cross product)
又称外积,结果会得到同时垂直于两个矢量的新矢量。常用于计算一个面的法线,也可以用来判断面是正面还是反面。
V1*V2=((y1*z2 – z1*y2, z1*x2 – x1*z2, x1*y2 – y1*x2))
注意:叉积不满足交换律和结合律,但满足反交换律,即a*b=-(b*a)。
3.4.3.叉积的模
叉积的长度等于两个矢量模相乘再乘以夹角的正弦值,即|a*b|=|a||b|sin夹角
注意:叉积不管是用左手坐标系还是右手坐标系,对于计算结果是不会产生影响的,只会影响在三维空间的视觉表现(比如当右手坐标系转换为左手坐标系时,计算结果不变,但是在渲染到屏幕上时,图像可能相反)

三、矩阵
1.什么是矩阵
一个矩阵可以把一个矢量从一个坐标空间转换到另一个坐标空间,从外观上就是一个长方形的网格,每个格子都放有一个数字。它是由m*n个标量组成的长方形数组。

只有一行的成为行矩阵,只有一列的成为列矩阵。
2.矩阵的运算
2.1.矩阵和矩阵的加减
前提:两个矩阵的行数和列数必须相同
对应位相加减

2.2.矩阵和标量的乘法
矩阵每一位都乘以标量

2.3.矩阵和矩阵的乘法
前提:矩阵和矩阵相乘时,只有满足第一个矩阵的列数和第二个矩阵的行数相等的条件时,才可以相乘。即r×n矩阵,只能和n×c矩阵相乘,得到的结果是一个r×c矩阵
相乘得到的结果矩阵的行数是第一个矩阵的行数,而列数是第二个矩阵的列数



注意:矩阵乘法一般不满足交换律,但一些特殊情况会存在,但满足结合律
3.特殊矩阵
3.1.方块矩阵
简称方阵,即行数和列数都相等的矩阵。
3.2.对角元素
方阵的对角元素指的是行号和列号相等的元素,比如M11、M22、M33
3.3.对角矩阵
如果一个方阵除对角元素外所有元素都为0,则这个矩阵叫做对角矩阵
3.4.单位矩阵
一个特殊的对角矩阵是单位矩阵,其对角元素都为1,且任何矩阵和它相乘结果都是原来的矩阵
即MI=IM=M

3.5.转置矩阵
实际上是对原矩阵的一种运算,即转置运算。即将同号数的行转换为同号数的列

转置矩阵的一些性质:

3.6.逆矩阵
前提:该矩阵必须是一个方阵,但不是所有方阵都有逆矩阵(比如所有元素都为0的方阵)
最重要的性质:矩阵和矩阵的逆矩阵相乘为一个单位矩阵

如果一个矩阵有对应的逆矩阵,则说这个矩阵是可逆的,或者说是非奇异的。反之就是不可逆的,或者说是奇异的
3.7.正交矩阵
正交矩阵是一种特殊的方阵,如果一个方阵和它的转置矩阵的乘积是一个单位矩阵,则称这个矩阵是正交的。

即如果一个矩阵是正交的,那么它的转置矩阵和逆矩阵是一样的。

4.矩阵的几何意义:变换
4.1.什么是变换
变换,指的是我们把一些数据(如点、方向矢量甚至是颜色等)通过某种方式进行转换的过程
4.2.变换类型
4.2.1.线性变换
线性变换指的是那些可以保留矢量和标量的变换(即可以保留矢量加和标量乘的变换),如缩放、旋转、错切、镜像、正交投影

对于所以的线性变换都可以用3x3的矩阵来表示
4.2.2.仿射变换
仿射变换就是合并线性变换和平移变换的变换类型,因为平移变换不包含于线性变换中,仿射变换就诞生了。
仿射变换可以用一个4x4矩阵来表示
为此,我们需要把矢量扩展到四维空间下,也就是齐次坐标空间下
齐次坐标
3x3矩阵不能表示平移操作,就必须扩展到4x4矩阵,那么就必须三维矢量转换到四维矢量。
对于点,三维坐标转换为齐次坐标系,w分量设为1

对于方向矢量,其w分量设为0

4.3.分解基础变换矩阵
我们可以使用一个4x4的矩阵来表示平移、旋转和缩放,我们把表示纯平移、纯旋转和纯缩放的变换矩阵叫做基础变换矩阵。
我们可以将这个基础变换矩阵分解成4个组成部分:

其中, 左上角的矩阵M 3 x 3 用于表示旋转和缩放, t 3x1 用于表示平移,0 1x3 是零矩阵, 即0 1 x 3 =[0, 0, 0],右下角的元素就是标量 1。
4.4.平移矩阵
我们可以用矩阵乘法来表示对一个点进行平移变换

而向量没有位置属性,平移向量不应该对向量产生影响

平移矩阵的逆矩阵就是反向平移得到的矩阵,即

4.5.缩放矩阵
我们可以对一个模型沿空间的x轴,y轴和z轴进行缩放,同样我们可以使用矩阵乘法来表示一个缩放变换。

对方向矢量可以使用同样的矩阵进行缩放,即

如果kx=ky=kz,则这样的缩放称为统一缩放,否则称为非统一缩放
缩放矩阵一般不是正交矩阵
4.6.旋转矩阵
绕x轴旋转:

绕y轴旋转

绕z轴旋转

旋转矩阵的逆矩阵是旋转相反角度得到的变换矩阵,旋转矩阵是正交矩阵,而且多个旋转矩阵间的串联同样正交
4.7.复合变换
我们可以把平移、旋转和缩放组合起来,形成一个复杂的变换过程。复合变换可以通过矩阵的串联来实现,且变换的结果是依赖于变换顺序的,又因为矩阵乘法不满足交换律,因此变换顺序很重要。

注意:大多数情况下,先进行缩放,再旋转,然后才是平移
四、坐标空间
1、坐标空间的变换
我们知道,要想定义一个坐标空间,必须明确其原点和三个坐标轴的方向,而这些数值实际上是相对另一个坐标空间的,每个坐标空间都是另一个坐标空间的子空间,反过来每个空间都有一个父坐标空间。对坐标空间的变换实际上就是在父空间和子空间对点和矢量进行变换。
2、模型空间(model space)
模型空间也称为对象空间或局部空间,是物体自身的坐标空间
每个模型都有自己独立的坐标空间,当模型移动或旋转的时候,模型空间也跟着移动或旋转
模型的顶点包含了顶点的位置坐标,这个坐标是相对于模型空间的原点定义的
模型空间的坐标原点和坐标轴由美术在建模软件中设置。
在没有手动调整时,一般情况坐标原点是在模型的重心位置。
模型空间中,我们会使用方向的概念,比如“前,后,左,右,上,下”,我们称为自然方向。
Unity在模型空间中使用的是左手坐标系,因此在模型空间中,+x轴、+y轴、+z轴分别对应模型的右、上、前方向,但需要注意的是,模型空间中的x轴、y轴、z轴和自然方向的对应不一定是这种关系。
3、世界空间(world space)
游戏中的场景角色都位于这个游戏世界空间中,光照模型的很多计算都在世界空间中进行。
在Unity中,世界空间使用了左手坐标系,但它的x轴、y轴、z轴是固定不变的。
4、观察空间(view space)
也称为摄像机空间,可以认为是模型空间的一个特例。观察空间是摄像机的模型空间,是一个三维空间,从观察空间到屏幕空间的转换需要经历一个操作就是投影。
观察空间使用的是右手坐标系。摄像机的前方指向-z轴方向。
5、裁剪空间(clip space)
也被称为齐次裁剪空间,用于变换的矩阵叫做裁剪矩阵,也被称为投影矩阵
裁剪的空间由视锥体决定,视锥体指的是空间中的一块区域,这块区域决定了摄像机可以看到的空间。视锥体由六个面包围而成,这些平面被称为裁剪平面。利用视锥体对不可见的图元进行剔除,摄像机看不到的地方就不渲染,不同的视锥体,对应不同投影类型。
正交投影:

透视投影:

在视锥体的6块裁剪平面中,有两块裁剪平面比较特殊,分别是近裁剪平面和远裁剪平面,它们决定了摄像机可以看到的深度范围。
6、屏幕空间(screen space)
裁剪完成后,就需要把视锥体的图元信息投影到二维的屏幕空间中。
7、顶点的坐标空间变换过程
顶点变换的第一步,就是将顶点坐标从模型空间转换到世界空间中,这个变换通常叫做模型变换(model transform)。
Unity的Transform组件可以调节模型的位置,如果Transform有父节点,那么Position就是在其父节点的模型空间的位置,如果没有父节点,Position就是在世界空间中的位置。
顶点变换的第二步,就是将顶点坐标从世界空间变换到观察空间中,这个变换通常叫做观察变换(view transform)。
为了得到顶点在观察空间中的位置,可以采取两种方法:一种是计算观察空间的三个坐标轴在世界空间下的表示,然后构建出从观察空间变换到世界空间的变换矩阵,再对该矩阵求逆来得到从世界空间变换到观察空间的变换矩阵。第二种就是想象平移整个观察空间,让摄像机原点位于世界坐标的原点,坐标轴与世界空间中的坐标轴重合即可。
顶点接下来就要从观察空间转换到裁剪空间中,然后再转换到屏幕空间中,其中裁剪空间的投影矩阵并不会真正的进行投影,而是对屏幕空间实施投影做投影准备。
8、空间转换顺序

9、法线变换
法线(normal),也被称为法矢量(normal vector)
切线(tangent),也被称为切矢量(tangent vector),与发现类似,切线往往也是模型顶点携带的一种信息,通常与纹理空间对齐,且与法线方向垂直。
如果直接使用变换顶点的变换矩阵来变换切线或者是法线,有可能得不到正确的结果(因为法线和切线都是方向矢量,不会受到平移变换的影响),我们可以使用原变换矩阵的逆转置矩阵来变换法线得到正确的结果。
值得注意的是,如果变换矩阵是正交矩阵,那么我们可以使用用于变换顶点的变换矩阵来直接变换法线;如果变换只包括旋转变换,那么这个变换矩阵就是正交矩阵,而如果变换只包含旋转和统一缩放而不包含非统一缩放,我们可以统一缩放系数k来得到变换矩阵的逆转置矩阵以避免计算逆矩阵的过程;如果变换中包含了非统一变换,我们就必须求解逆矩阵来得到变换发现的矩阵。
五、Unity Shader的内置变量(数学)
使用Unity写Shader的一个好处在于它提供了很对内置的参数,使得我们不再需要自己手动计算一些值。在一些不同的Unity版本中,一些内置变量可能会有一些不同。文章来源:https://www.toymoban.com/news/detail-770904.html
Unity内置的变换矩阵(版本:5.2)文章来源地址https://www.toymoban.com/news/detail-770904.html
| 变量名 | 描述 |
| UNITY_MATRIX_MVP | 当前的模型观察投影矩阵,用于将顶点/方向矢量从模型空间变换到裁剪空间 |
| UNITY_MATRIX_MV | 当前的模型观察矩阵,用于将顶点/方向矢量从模型空间变换到观察空间 |
| UNITY_MATRIX_V | 当前的观察矩阵,用于将顶点/方向矢量从世界空间变换到观察空间 |
| UNITY_MATRIX_P | 当前的投影矩阵,用于将顶点/方向矢量从观察空间变换到裁剪空间 |
| UNITY_MATRIX_VP | 当前的观察投影矩阵,用于将顶点/方向矢量从世界空间变换到裁剪空间 |
| UNITY_MATRIX_T_MV | UNITY_MATRIX_MV的转置矩阵 |
| UNITY_MATRIX_IT_MV | UNITY_MATRIX_MV的逆转置矩阵,用于将法线从模型空间变换到观察空间,也可以用于得到UNITY_MATRIX_MV的逆矩阵 |
| _Object2World | 当前的模型矩阵,用于将顶点/方向矢量从模型空间变换到世界空间 |
| _World2Object | _Object2World的逆矩阵,用于将顶点/方向矢量从世界空间变换到模型空间 |
到了这里,关于UnityShader(三)数学基础的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!