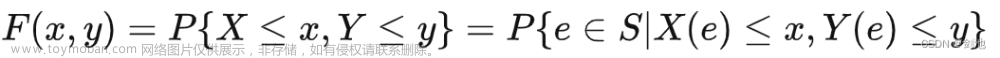深度学习-必备的数学知识-概率论2-Toy模板网

这篇具有很好参考价值的文章主要介绍了深度学习-必备的数学知识-概率论2。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

深度学习

必备的数学知识

概率论

在上一篇文章中，我带大家初略的了解了概率论是什么。这篇文章中我将为大家讲解概率论中的随机变量和概率分布。

随机变量

在概率论中，随机变量（random variable）是一个可以随机地取不同值的变量。一个随机变量是对可能的状态的描述，它的取值范围是事件的所有可能的状态。它必须伴随着概率分布来指定每个状态的可能性。随机变量可以是离散的，也可以是连续的，取决于它的值是否可以在一个连续的范围内变化。

离散型随机变量的例子有：掷骰子的结果，1到6的整数

连续型随机变量的例子有：一个人的体重，一个人的体重可以在一个连续的范围内取任何值。

概率分布

概率分布（probability distribution）用来描述随机变量在每一个可能取到的状态的可能性。换句话说，概率分布是描述随机变量可能的取值及其对应概率的函数。
对于离散型随机变量和连续型随机变量使用不同的方式描述。

概率质量函数

对于离散型随机变量的概率分布可以用概率质量函数描述（probability mass function,PMF）。我们通常使用大写字母P来描述概率质量函数。通常每一个随机变量都有着不同的概率密度函数，也就是说概率密度函数是不通用的。我们不通过函数名来推断所使用的概率密度函数，而是通过随机变量来推断。如 $P (x)$ 与 $P (y)$ 是不一样的。

$x = x$ （前一个x是随机变量本身，后一个是随机变量的取值）的概率密度函数记作 $P (x)$ ，通常我们明确写出随机变量的名称来避免混淆，如： $P (x = x)$ 。使用~符号表示随机变量遵循的概率密度函数，如：$x $ ~ $P (x)$ 。

概率密度函数是将随机变量能取到的每个状态映射到随机变量取得该状态的概率，概率为1表示x=x是必然发生的，概率为0表示x=x是不可能发生。

如果一个函数P是随机变量的概率密度函数，则必须满足以下三个条件

函数的定义域是随机变量所有可能的状态的集合
$\forall x \in x$ , $0\leq P(x) \leq 1$ ,必然发生的事概率为1，不存在比这概率还大的；必然不可能发生的事件的概率是0，不存在比这概率还小的。
$\sum_{x \in x} P(x)=1$ ,随机变量的能取到的所有可能的状态的概率加起来等于1。这称为归一化（normalized）。

我们再拿出掷骰子这个例子。我们用随机变量x表示掷骰子的结果，它一共有6个不同的状态( $x_1,x_2,..,x_6$ )。在理想情况下，x是均匀分布的，也就是它的每一个状态是等可能的。此时我们可以将x的PMF设为
$P(\texttt{x}=x_i)=\frac{1}{6}$
这个函数满足上述的条件，这很容易就可以看出来。

概率质量函数可以用于多个随机变量，如 $P (x = x, y = y)$ ,它表示的是当x=x，y=y同时发生的概率，我们也可以简写为P(x,y)。这称为联合概率分布

概率密度函数

对于连续性随机变量的概率分布我们使用概率密度函数（probability density function，PDF）。概率密度函数 $P (x)$ 并没有直接给出特定状态的概率。这是因为连续性随机变量，它的可能的状态是无限多的，以至于取到某一个特定的状态的概率为0。概率密度函数 $P (x)$ 给出的是随机变量落在x附近无穷小的区间的概率。具体来说，如果Δx是一个很小的正数，那么X落在[x, x+Δx]内的概率近似等于p(x)Δx。

我们可以通过 $P (x)$ 对某个区间区间[a,b]求积分来获得x落在区间中的概率，
$\int_{a}^{b}P(x)dx$

概率密度函数需要满足以下条件：文章来源地址https://www.toymoban.com/news/detail-771608.html

函数的定义域是随机变量所有可能的状态的集合
$\forall x \in x$ , $\geq 0$ ，PDF表示的是随机变量在某个特定值附近的概率密度，所有PDF值可以大于1/
$\int P(x)dx=1$ ，随机变量x的任意可能的状态它必然会落到定义域中。这反映了所有可能事件的概率之和为1的事实。
联合概率分布对于概率密度函数同样成立。对于多个随机变量，我们可以定义联合概率密度函数，它描述了这些随机变量同时取特定值的概率密度。