1.概述
1.1 算法的概念
算法设计应满足的目标:正确性,可使用,可读,健壮,高效率,低存储
算法的5个重要特征:有限、确定、可行、输入、输出
通常用函数的返回值表示算法能否正确执行,如果某个形参需要将执行结果回传给实参,需要将该形参设计为引用型参数
1.2 算法分析
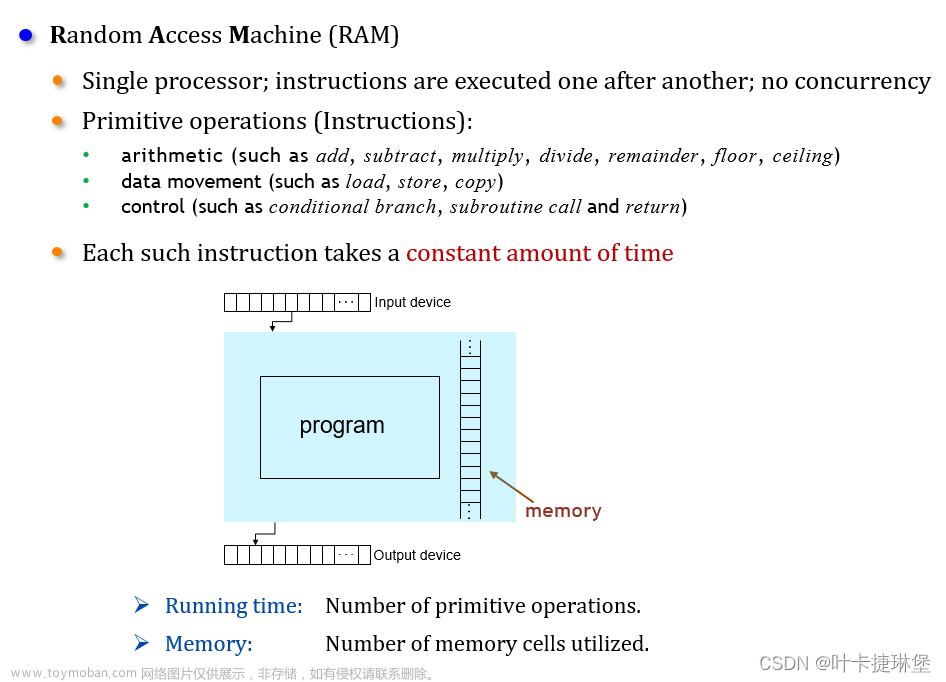
算法分析是分析算法占用计算机资源的情况
算法分析的两个主要方面是分析算法的时间复杂度和空间复杂度
1.3 时间复杂度
一层循环:
- 列出循环趟数t与每趟循环i的变化值
- 找出t与i的关系(公式什么的)
- 找出循环结束条件
- 联立两式,解方程



两层循环
- 列出外层循环i的变化值
- 列出内层语句的执行次数
- 内层语句执行次数*外层循环次数=结果

多层循环
方法1. 抽象为计算三维体积
方法2. 列式求和
1.4 空间复杂度
能不递归就不递归,递归占用的空间和时间复杂度太高了
循环占用的空间至始至终都是那个,但递归每次的函数空间都是新创的,就是不能重复利用。
2.选择题
-
衡量一个算法好坏的标准是(C )。
A 运行速度快 B 占用空间少 C 时间复杂度低 D 代码短 -
二分搜索算法是利用( A )实现的算法。
A、分治策略 B、动态规划法 C、贪心法 D、回溯法 -
以下不可以使用分治法求解的是(D )。
A 棋盘覆盖问题 B 选择问题 C 归并排序 D 0/1背包问题 -
实现循环赛日程表利用的算法是( A )。
A、分治策略 B、动态规划法 C、贪心法 D、回溯法 -
实现棋盘覆盖算法利用的算法是( A )。
A、分治法 B、动态规划法 C、贪心法 D、回溯法 -
实现合并排序利用的算法是( A )。
A、分治策略 B、动态规划法 C、贪心法 D、回溯法 -
使用分治法求解不需要满足的条件是(A )。
A 子问题必须是一样的 B 子问题不能够重复C 子问题的解可以合并 D 原问题和子问题使用相同的方法解 -
下列不是动态规划算法基本步骤的是( A )。
A、找出最优解的性质 B、构造最优解 C、算出最优解 D、定义最优解 -
下列是动态规划算法基本要素的是( D )。
A、定义最优解 B、构造最优解 C、算出最优解 D、子问题重叠性质 -
最长公共子序列算法利用的算法是( B )。
A、分支界限法 B、动态规划法 C、贪心法 D、回溯法 -
实现最大子段和利用的算法是( B )。
A、分治策略 B、动态规划法 C、贪心法 D、回溯法 -
矩阵连乘问题的算法可由( B)设计实现。
A、分支界限算法 B、动态规划算法 C、贪心算法 D、回溯算法 -
下列算法中通常以自底向上的方式求解最优解的是( B )。
A、备忘录法 B、动态规划法 C、贪心法 D、回溯法 -
最大效益优先是( A )的一搜索方式。
A、分支界限法 B、动态规划法 C、贪心法 D、回溯法 -
下面不是分支界限法搜索方式的是( D )。
A、广度优先 B、最小耗费优先 C、最大效益优先 D、深度优先 -
广度优先是( A )的一搜索方式。
A、分支界限法 B、动态规划法 C、贪心法 D、回溯法 -
一个问题可用动态规划算法或贪心算法求解的关键特征是问题的( B )。
A、重叠子问题 B、最优子结构性质 C、贪心选择性质 D、定义最优解 -
贪心算法与动态规划算法的主要区别是( B )。
A、最优子结构 B、贪心选择性质 C、构造最优解 D、定义最优解 -
( D )是贪心算法与动态规划算法的共同点。
A、重叠子问题 B、构造最优解 C、贪心选择性质 D、最优子结构性质 -
背包问题的贪心算法所需的计算时间为( B )。
A、O(n2n) B、O(nlogn) C、O(2n) D、O(n) -
0-1背包问题的回溯算法所需的计算时间为( A )
A、O(n2n) B、O(nlogn) C、O(2n) D、O(n) -
下列算法中通常以深度优先方式系统搜索问题解的是( D )。
A、备忘录法 B、动态规划法 C、贪心法 D、回溯法 -
下面是贪心算法的基本要素的是( C )。
A、重叠子问题 B、构造最优解 C、贪心选择性质 D、定义最优解 -
下面问题(B )不能使用贪心法解决。
A 单源最短路径问题 B N皇后问题 C 最小花费生成树问题 D 背包问题 -
下列算法中不能解决0/1背包问题的是(A )
A 贪心法 B 动态规划 C 回溯法 D 分支限界法 -
回溯法解TSP问题时的解空间树是( A )。
A、子集树 B、排列树 C、深度优先生成树 D、广度优先生成树 -
回溯法的效率不依赖于下列哪些因素( D )
A.满足显约束的值的个数 B. 计算约束函数的时间
C. 计算限界函数的时间 D. 确定解空间的时间 -
下面哪种函数是回溯法中为避免无效搜索采取的策略( B )
A.递归函数 B.剪枝函数 C.随机数函数 D.搜索函数 -
以深度优先方式系统搜索问题解的算法称为 ( D ) 。
A、分支界限算法 B、概率算法 C、贪心算法 D、回溯算法 -
回溯法搜索状态空间树是按照(C )的顺序。
A 中序遍历 B 广度优先遍历 C 深度优先遍历 D 层次优先遍历
3.分治法
3.1 快速排序 (*)
#include <stdio.h>
#define SIZE 6
//快速排序
void quick_sort(int num[], int low, int high )
{
int i,j,temp; //temp是用来当找到i和j并且i!=j时交换i和j的值
int tmp; //tmp用来保存基准数
i = low; //num[low]也是基准数
j = high;
tmp = num[low]; //任命为中间分界线,左边比他小,右边比他大,通常第一个元素是基准数
if(i > j) //如果下标i大于下标j,函数结束运行,这个一般出现在以分界线为轴之后,左边或者把右边只有一个数
{
return;
}
while(i != j)
{
while(num[j] >= tmp && j > i)
{
j--;
}
while(num[i] <= tmp && j > i)
{
i++;
}
if(j > i)
{
temp = num[j];
num[j] = num[i];
num[i] = temp;
}
}
// 直到i==j时
num[low] = num[i];
num[i] = tmp;
quick_sort(num,low,i-1);
quick_sort(num,i+1,high);
}
int main()
{
//创建一个数组
int num[SIZE];
int i;
//输入数字
for(i =0; i < SIZE; i++)
{
scanf("%d",&num[i]);
}
quick_sort(num, 0, SIZE-1);
for(i = 0; i < SIZE; i++)
{
printf(" %d ", num[i]);
}
return 0;
}
移动方法:
- 在数组中选一个基准数tmp(通常为数组第一个);
- 数组中设置两个哨兵i(初始指向数组第一个)和j(初始指向数组最后一个);
- 先移动j,一次一次往前移,直到找到比tmp小的值(j>=tmp时都要往前移);
- 再移动i,一次一次往后移,直到找到比tmp大的值(i<=tmp时都要往后移);
- 当找到符合条件的i和j的值时,i和j对应的值互换,但是i和j指向的位置没变;
- 当i=j时,将i与tmp的值互换,i指向的位置没变;
- 体现分治的地方来了:此时,以i指向的数作为轴,分开左右两部分,每部分再按照上面的7个步骤再来一遍。
学习引用-快速排序
4.蛮力法
4.1 任务分配问题 (*)
问题描述:假设有n个任务需要分配给n个人执行,每个任务只分配给一个人,每个人只分配一个任务,且第j个任务分配给第i个人的成本是C[i,> j](1≤i , j≤n),任务分配问题要求找出总成本最小的分配方案。
用蛮力法解决任务分配生成成本矩阵,成本矩阵中相应元素相加来求得每种分配方案的总成本
相应解释看代码
#include <iostream>
#include <cstring>
using namespace std;
int visit[11],num[11];
int n,value = 9999999;
int martrix[4][4];
int lowNum[11];
/*检验数据
4
9 2 7 8
6 4 3 7
5 8 1 8
7 6 9 4
*/
// 这个函数用于每一次在确定了num数组之后进行对应的总成本计算
void findLowCost() {
int sum = 0;
for(int i = 1; i <= n; i++) {
sum += martrix[i - 1][num[i] - 1];
}
if(sum < value) {
for(int i=1;i<=n;i++){
lowNum[i]=num[i];
}
value = sum;
}
}
/*
visit代表当前i任务是否被选择
i的取值:1,2,3,4;代表任务种类
num数组代表人员,
num[length]:里面的length代表第几个人,用1,2,3,4区分,共四个人
*/
void dfs(int length) {
if(length > n) {
findLowCost();
} else {
for(int i = 1; i <= n; i++) {
if(visit[i] == 0) {
visit[i] = 1; //visit[i]=1代表当前i任务是否被选择
num[length] = i; //num[length] = i代表第length个人选择了第i个任务
dfs(length + 1);
visit[i] = 0;
//visit[i]重新置为0,代表在一次分配方案之后
//(就是每个人都分配到一种任务,每个任务只分配给一个人)
//当length > n进行了findLowCost函数之后,回退至length=n-1,以为length==n的那个循环已经走完了
//在 length=n-1时,visit置0,,但还有一个i需要走循环,这又是一个方案
// 依次循环回退走完所有方案。
}
}
}
}
int main() {
cin >> n;
memset(visit,0,sizeof(visit)); //visit全置为0,代表任务全没被选择
for(int i = 0; i < 4; i++) {
for(int j = 0; j < 4; j++) {
cin >> martrix[i][j];
}
}
dfs(1);
cout<<"最小成本分配方案:"<<endl;
for(int i=1;i<=n;i++){
cout<<"第"<<i<<"个人选择的任务是:"<<lowNum[i]<<endl;
}
cout << "最小成本:" <<value;
return 0;
}
学习引用-任务分配蛮力法
5.回溯法
5.0 回溯法的概念
在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时(设置的判断条件称为“剪枝函数”),就往回移动(回溯),尝试别的路径
回溯法思路的简单描述是:把问题的解空间转化成了图或者树的结构表示,然后使用深度优先搜索策略进行遍历,遍历的过程中记录和寻找所有可行解或者最优解。
与分支限界法的联系:使用剪枝函数的深度优先生成状态空间树中的节点的求解方法称为回溯法;广度优先生成结点,并使用剪枝函数的方法称为分枝限界法
5.1 装载问题 (*)
- 问题描述:现有 n 件货物 (Cargo) 每件货物的重量(weight)是 Wi ( 0<i≤n , i∈ N ), 需要把这 n 件货物全部装上两艘船 shipOne 和 shipTwo , 两艘船的最大容量为Capacity1 和 Capacity2 问是否有一种合理的方案使得全部货物都能装上船?
- 代码
package com.ljh;
class Cargo {
int weight = 0; //货物重量
boolean isLoad = false; //货物是否被装载上船状态
}
class Ship {
int capacity = 0; //船的容量
int minMargin; //目前得到的最小余量(不断缩小)-就是剩余的船的容量的最小值
int nowMargin; //现在的船上余量
int nowWeight; //现在船上货物的重量
int numOfCargo; //船上货物数量
Cargo[] cargo;
Cargo[] realCargo;
public Ship(int capacity) {
this.capacity = capacity;
this.minMargin = capacity;
this.nowMargin = capacity;
}
//这里使用重载是为了区分两艘船的作用.
public Ship(int capacity, Cargo cargo[], Cargo realCargo[]) {
this.capacity = capacity;
this.cargo = cargo;
this.realCargo = realCargo;
this.numOfCargo = cargo.length; //初始化时船上的货物个数=总货物个数
this.minMargin = capacity;
this.nowMargin = capacity;
this.nowWeight = 0;
}
}
public class BackTrackAlgorithm {
//声明全部所需的变量,我们需要装载的货物重量,它的总重量,两艘船,货物对象.
static int aboutCargo[] = {90, 80, 40, 30, 20, 12, 10};
static int totalWeight;
static Ship shipOne;
static Ship shipTwo;
static Cargo[] cargo = new Cargo[aboutCargo.length]; //声明cargo数组
static Cargo[] realCargo = new Cargo[aboutCargo.length]; //不用先思考readlCargo的作用在后面会给出解释
static int i = 0; //见后
//在main中直接调用两个方法得出解
public static void main(String[] args) {
BackTrackAlgorithm bta = new BackTrackAlgorithm();
bta.init();
bta.getResult();
}
//初始化船,并使用回溯法,使得我们的问题得出最优方案
public void init() {
for (int j = 0; j < aboutCargo.length; j++) {
cargo[j] = new Cargo();
realCargo[j] = new Cargo();
realCargo[j].weight = aboutCargo[j];
cargo[j].weight = aboutCargo[j];
totalWeight += aboutCargo[j]; //计算总的货物重量
}
shipOne = new Ship(152, cargo, realCargo); //这里代表我先以shipOne做考虑
shipTwo = new Ship(130);
//开始建立树结构
while (true) {
//进行每一轮的选择
while (i < shipOne.numOfCargo) {
if ((shipOne.nowWeight + shipOne.cargo[i].weight) <= shipOne.capacity) {//判断条件
shipOne.nowWeight += shipOne.cargo[i].weight;//变化当前重量
shipOne.nowMargin -= shipOne.cargo[i].weight;//变化当前余量
shipOne.cargo[i].isLoad = true;//确认i货物装载上船
i += 1;
} else {
shipOne.cargo[i].isLoad = false;//不装载,继续往下走
i += 1;
}
}
//经过上面已经得到shipOne的一个方案
//进行一轮的选择之后是否得到更优的方案
//这里改变realCargo[j].isLoad才是代表真正最优方案
if (shipOne.nowMargin < shipOne.minMargin) {
shipOne.minMargin = shipOne.nowMargin;
//如果得到更优的方案,我们需要存入这一轮的货物选择情况,为什么要使用另一个realCargo数组,请阅读代码后思考片刻
for (int j = 0; j < shipOne.numOfCargo; j++) {
if (shipOne.cargo[j].isLoad == true) {
shipOne.realCargo[j].isLoad = true;
}
if (shipOne.cargo[j].isLoad == false) {
shipOne.realCargo[j].isLoad = false;
}
}
}
//进入回溯法,回溯的就是我们之前设置的静态属性 i 即我们选择的货物货号
i = backtrace(i - 1);//为什么是 i-1:i-1才是判断的最后一个货物货号
//退出的条件,我们是否已经结束最后一轮.
if (i == 0) {
return;
}
}
}
//回溯法
public int backtrace(int j) {
//请读者思考作用.
while (j > 0 && shipOne.cargo[j].isLoad == false) {
j -= 1;
}
//请读者思考作用.
if (shipOne.cargo[j].isLoad == true) {
shipOne.cargo[j].isLoad = false;
shipOne.nowMargin += shipOne.cargo[j].weight;
shipOne.nowWeight -= shipOne.cargo[j].weight;
j += 1;
}
return j;
/**
* tips:这里每轮的回溯会改变shipOne.cargo[i].isLoad,最后得到的自然是最后一轮选择方案,
* 但最后一轮得到的不一定是最优解,所以我们肯定需要另外一个Cargo数组来记录更优方案 即前面
* 声明的readCargo[]
*/
}
//返回最优结果集
public void getResult() {
//判断是否有解
if ((totalWeight - (shipOne.capacity - shipOne.minMargin)) <= shipTwo.capacity) {
System.out.println("\n本问题有合理的方案.\n");
for (int j = 0; j < aboutCargo.length; j++) {
if (shipOne.realCargo[j].isLoad == true) {
System.out.println("货物 " + j + " 已经装载上船1,重量是:" + shipOne.realCargo[j].weight);
}
if(shipOne.realCargo[j].isLoad==false) {
System.out.println("货物 " + j + " 将会装载上船2,重量是:" + shipOne.realCargo[j].weight);
}
}
} else {
System.out.println("经过努力的尝试,得出本问题没有合理的方案使得全部货物装上两艘船,抱歉");
}
}
}
解题思路:
回溯法是将问题的 解 抽象成 图或者树的结构来表示.
在装载问题中,对于每个货物我们的选择只有 选择 / 不选 所以我们选择抽象成树的结构,对于选择此货物自然对应 1/true
对于不选择此货物对应 0/true , 依次对每个货物进行选择,我们自然会得到 2^n个解 但是我们当然没有必要把所有结果都列举出来,
例如以下例子 :W 为货物的重量的集合c1,c2为两艘船的总容量,设置判断条件为: 已经装上的 货物重量 加上 下一个货物
后的重量不大于shipOne的容量,那么就可以装上此货物 .若大于则选择不装此货物 这样自然就可以得到一棵得到 优化结果集的子树 .但是经过第一轮的选择之后,虽然得到了第一个方案,但是我们不能保证这是最优的解 , 不能确定是最优的方案就不能保证我们的问题是否有解 ,
所以只有经过多轮不同的选择 才能得到最优的方案,才能得出问题是否有解.那么 , 如何进行多轮的选择? 怎么才能知道 哪一轮选择的方案是最好的? 前面提到余容量就是我们判断是否是更优方案的指标
剩余容量越小,则说明这样的方案更优.知道如何判断是否是更优的方案之后,我们就要思考如何遍历这棵树能更快的得出结果集,如果从头开始遍历,自然是效率最低选择,因为我们会重复走我们已经走过的路.
所以我们不妨进行回溯, 如下图所示: 我们第一轮得出的结果是90+0+40+0+20+0+0 ,于是从最后一个货物 ( 重量为10的货物开始回溯 ) 对于已经选择为 0/false
的物品我们自然不需要再去遍历它的左子树了,因为我们本身就装不下它 . 所以我们去遍历右子树 . 于是我们往上回溯 ,
找到以第一个我们已经选择的货物 ,我们这一轮 ( 第二轮从选择重量为20的货物开始 ) 就不装载 重量为 20的货物,
我们想要去选择剩下的其余货物(12 和 10).进行第二轮的选择后 会得到一个解决方案,我们自然就可以比较 余量(Margin)
是否较前一种方案更优 接着我们继续回溯…一直到我们进行最后一轮回溯 , 最后一轮便是从我们之前选择的第一个货物开始,一来就不装载 (
重量为90的货物 ) 此货物. 最后进行一轮选择. 最后就可以得到我们的最优方案 , 以此便可以确定我们的问题 , 是否有解.
左子树有值代表选中,左子树为0代表未选中
学习引用-装配问题回溯法
6.分支限界法
6.1 流水作业调度问题 (*)
问题描述:有n个作业(编号为1~n)要在由两台机器M1和M2组成的流水线上完成加工。每个作业加工的顺序都是先在M1上加工,然后在M2上加工。M1和M2加工作业i所需的时间分别为ai和bi(1≤i≤n)。
流水作业调度问题要求确定这n个作业的最优加工顺序,使得从第一个作业在机器M1上开始加工,到最后一个作业在机器M2上加工完成所需的时间最少。可以假定任何作业一旦开始加工,就不允许被中断,直到该作业被完成,即非优先调度
关键公式:对于按1~n顺序执行的某种调度方案,f1表示在M1上执行完当前第i步的作业对应的总时间,f2数组表示在M2上执行完当前第i步的作业的总时间。
若第i步执行作业j,计算公式如下:
f1=f1+a[j];
f2[i]=max(f1,f2[i-1])+b[j]
代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
#define INF 999999
#define MAX 5
using namespace std;
//问题表示
int n=4; //作业数
int a[MAX]={0,5,10,9,7};//M1上的执行时间,不用下标0的元素
int b[MAX]={0,7,5,9,8};//M2上的执行时间,不用下标0的元素
//求解结果表示
int bestf=INF;//存放最优调度时间
int bestx[MAX];//存放当前作业最佳调度
int total=1;//结点个数累计
struct NodeType//队列结点类型
{
int no;//结点编号
int x[MAX];//x[i]表示第i步分配作业编号
int y[MAX];//y[i]=1表示编号为i的作业已经分配
int i;//步骤编号
int f1;//f1表示在M1上执行完当前第i步的作业对应的总时间
int f2;//f2表示在M2上执行完当前第i步的作业的总时间
int lb;//下界
bool operator<(const NodeType &s) const//重载<关系函数
{
return lb>s.lb;//lb越小越优先出队
}
};
void bound(NodeType &e)//求结点e的限界值
{
int sum=0;
for(int i=1;i<=n;i++)//扫描所有作业
{
if(e.y[i]==0) //编号为i的作业未分配
{
sum+=b[i];//仅累计e.x中还没有分配的作业的在M2上的执行时间
}
}
e.lb=e.f1+sum;
}
void bfs()//求解流水作业调度问题
{
NodeType e,e1; priority_queue<NodeType> qu;//定义优先队列
memset(e.x,0,sizeof(e.x));//初始化根结点的x
memset(e.y,0,sizeof(e.y));//初始化根结点的y
e.i=0;//根结点
e.f1=0;
e.f2=0;
bound(e);
e.no=total++;
qu.push(e);//根结点进队列
while(!qu.empty())
{
e=qu.top();
qu.pop(); //出队结点e
if(e.i==n) //达到叶子结点
{
if(e.f2<bestf) //比较求最优解
{
bestf=e.f2;
for(int j1=1;j1<=n;j1++)
{
bestx[j1]=e.x[j1];//在第j1步分配对应的作业
}
}
}
e1.i=e.i+1;//扩展分配下一个步骤的作业,对应结点e1
for(int j=1;j<=n;j++)//考虑所有的n个作业
{
if(e.y[j]==1)
{
continue;//作业j是否已分配,若已分配,跳过
}
//若作业j还未被分配:
for(int i1=1;i1<=n;i1++)//复制e.x得到e1.x
{
e1.x[i1]=e.x[i1];
}
for(int i2=1;i2<=n;i2++)//复制e.y得到e1.y
{
e1.y[i2]=e.y[i2];
}
e1.x[e1.i]=j;//为第i步分配作业j
e1.y[j]=1;//表示作业j已经分配
e1.f1=e.f1+a[j];//求f1=f1+a[j]
e1.f2=max(e.f2,e1.f1)+b[j];//求f[i+1]=max(f2[i],f1)+b[j]
bound(e1);
if(e1.f2<=bestf)//剪枝,剪去不可能得到更优解的结点
{
e1.no=total++;//结点编号增加1
qu.push(e1);
}
}
}
}
int main()
{
bfs();
cout<<"Optimal plan is :"<<endl;
for(int k=1;k<=n;k++)
{
cout<<"The "<<k<<" step is to execute the job is :"<<bestx[k]<<endl;
}
cout<<"The total time is :"<<bestf<<endl;
return 0;
}
学习引用-流水作业分支界限法
7.贪心法
7.0 贪心算法的理解
贪心算法并不从整体最优上加以考虑,所作出的仅是某种意义上的局部最优选择,要确定一个问题是否适合使用贪心算法解题,必须证明每一步所做的贪心选择最终导致问题的整体最优解
7.1 活动安排问题 (*)
由于输入的活动是以其完成时间升序排列的,所以每次总是选择具有最早完成时间的活动加入集合 selected 中
代码:
#include <stdio.h>
#define N 100
/*检验数据
11
1 4
3 5
0 6
5 7
3 8
5 9
6 10
8 11
8 12
2 13
11 14
*/
/*
n:活动个数
s:开始时间数组
t:结束时间数组
selected:活动选择数组
*/
void greedyselector(int n, int s[], int f[], int selected[])
{
int i;
int j = 1; //j记录最近一次加入到a中的活动
selected[1] = 1; //首先选择活动1
for (i = 2; i <= n; i ++)
if (s[i] >= f[j]) { //如果活动i与活动j兼容,则选择活动i
// 兼容性的判断:下一个活动的开始时间>=上一个活动的结束时间
selected[i] = 1;
j = i;
}
else
selected[i] = 0;
}
int main()
{
int s[N], f[N]; //s[i],f[i]存储活动 i的开始和结束时间
int selected[N]; //若活动 i被选择,则selected[i]置1,否则置0
int n,i;
printf("请输入活动个数:");
scanf("%d", &n);
printf("请输入各个活动的开始和结束时间(要求按结束时间升序输入):\n");
for (i = 1; i <= n; i ++) //从i=1开始扫描
scanf("%d%d", &s[i], &f[i]);
greedyselector(n, s, f, selected);
printf("如下活动被选择:\n");
for (i = 1; i <= n; i ++)
if (selected[i] == 1)
printf("%d ", i);
printf("\n");
return 0;
}
学习引用-活动安排贪心算法
8.动态规划法
8.0 什么是动态规划:
动态规划是一种解决多阶段决策问题的优化方法,把多阶段过程转化为一系列单阶段问题
8.1 0/1背包问题 (*)
这个问题是有个前提条件:就是每个物品你最多只能拿一次(也就是说一个物品你要吗不拿就是拿0次,拿就只能拿1次,所以叫0/1问题)
递推树
状态转移方程
代码:
package com.ljh;
public class package01_DP {
/**
* 0-1背包
*
* @param val 价值
* @param weight 重量
* @param W 背包容量
* @return 最优解
*/
public static int MaxValueWithDP(int[] val, int[] weight, int W) {
int N = weight.length; //物品数
// 创建背包矩阵,矩阵的行数是物品数量+1;矩阵的列数是物品重量+1
int[][] V = new int[N + 1][W + 1];
//初始化矩阵第一行,背包容量为0
for (int col = 0; col <= W; col++) {
V[0][col] = 0;
}
//初始化矩阵第一列,背包容量为0
for (int row = 0; row <= N; row++) {
V[row][0] = 0;
}
for (int i = 1; i <= N; i++) { //一行一行填充值,i = 1从第二行开始填
for (int j = 1; j <= W; j++) { //一列一列填充值,j = 1从第二列开始填
if (weight[i - 1] <= j) { //如果当前物品重量小于等于背包中的当前重量 i为1是,weight[0]是第一个物品的重量
/*比较不加入该物品时该重量的最大价值(前一行)V[i - 1][j]
*与
*当前物品的价值val[i - 1]+没放该物品之前,背包已有重量的最大价值V[i - 1][j - weight[i - 1]]
*/
V[i][j] = Math.max(val[i - 1] + V[i - 1][j - weight[i - 1]], V[i - 1][j]);
} else { //如果当前物品重量大于背包中的当前重量
V[i][j] = V[i - 1][j]; //直接使用前一行的最优解
}
}
}
// 打印矩阵
for (int[] rows : V) {
for (int col : rows) {
System.out.format("%5d", col);
}
System.out.println();
}
return V[N][W];
}
public static void main(String[] args) {
int val[] = {3, 4, 5, 8}; //物品价值数组
int weight[] = {2, 3, 4, 5}; //物品重量数组
int W = 8; //背包重量
int MaxValue = MaxValueWithDP(val, weight, W);
System.out.println("当前背包的最大价值是:" + MaxValue);
}
}
根据代码做出动态转移表
文章来源:https://www.toymoban.com/news/detail-772376.html
学习引用-0/1背包问题动态规划法文章来源地址https://www.toymoban.com/news/detail-772376.html
到了这里,关于算法设计与分析-期末复习经典例题的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!