✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,
代码获取、论文复现及科研仿真合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
更多Matlab完整代码及仿真定制内容点击👇
智能优化算法 神经网络预测 雷达通信 无线传感器 电力系统
信号处理 图像处理 路径规划 元胞自动机 无人机
🔥 内容介绍
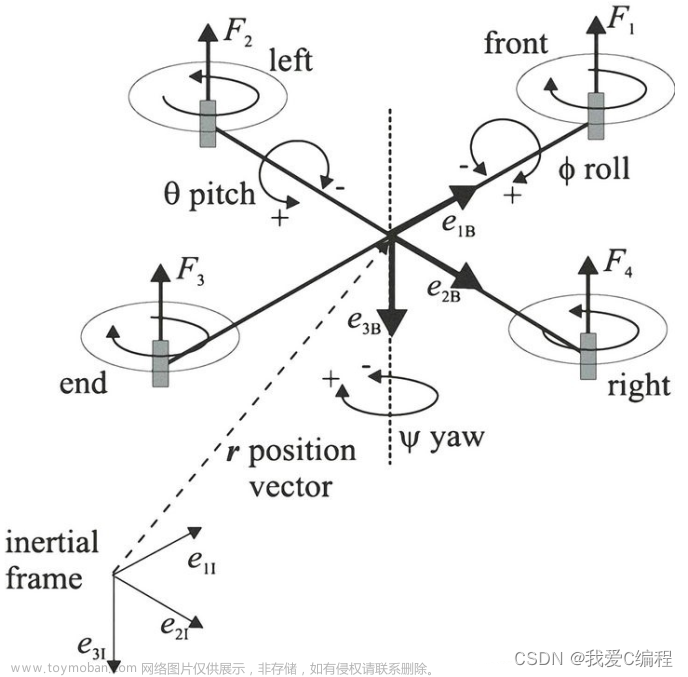
很高兴能够与大家分享关于使用ode45实现四旋翼无人机姿态仿真的内容。在本文中,我们将深入探讨无人机技术的发展以及如何利用ode45这一数值求解器来实现四旋翼无人机的姿态仿真。无人机技术近年来得到了迅猛发展,它在军事、民用、科研等领域都有着广泛的应用。无人机的姿态控制是其关键技术之一,通过仿真可以更好地理解和优化无人机的飞行性能。
首先,让我们来了解一下ode45数值求解器。ode45是MATLAB中用于求解常微分方程组的函数,它采用的是一种基于龙格-库塔法的显式Runge-Kutta方法。这种方法在数值计算中有着广泛的应用,能够有效地求解微分方程组,因此也适用于无人机姿态仿真的实现。
四旋翼无人机是一种常见的无人机类型,它由四个对称分布的螺旋桨提供动力,并通过调节螺旋桨的转速来实现飞行姿态的控制。在进行姿态仿真时,我们需要考虑无人机的动力学模型、姿态控制算法以及外部环境等因素。通过建立相应的数学模型,并利用ode45数值求解器进行仿真,我们可以模拟出无人机在不同飞行状态下的姿态变化,进而验证姿态控制算法的有效性。
在实际的仿真过程中,我们需要考虑无人机的动力学方程、姿态控制算法以及传感器等方面的模型。通过将这些模型整合在一起,并利用ode45进行数值求解,我们可以得到无人机在不同飞行条件下的姿态响应。这有助于我们更好地理解无人机的飞行特性,并为无人机的设计与控制提供重要的参考。
除了基于ode45的数值仿真方法,近年来还出现了许多其他无人机姿态仿真的研究成果。例如,基于飞行器动力学模型的仿真研究、基于控制算法的仿真优化等方面的工作。这些研究成果为无人机技术的发展提供了重要的支持,也为无人机在军事、民用等领域的应用提供了更加可靠的技术支持。
总的来说,无人机技术的发展离不开对其姿态控制技术的深入研究和实践。通过利用ode45数值求解器进行四旋翼无人机姿态仿真,我们可以更好地理解无人机的飞行特性,进而为无人机的设计与控制提供重要的参考。希望本文能够对无人机技术的研究与应用有所帮助,也期待未来能够看到更多关于无人机姿态仿真方面的深入研究成果。
📣 部分代码
function [t_out, s_out] = simulation_2d(controlhandle, trajhandle)video = true;params = sys_params;% real-timereal_time = true;%% **************************** FIGURES *****************************disp('Initializing figures...')if videovideo_writer = VideoWriter('test_control_2d.avi', 'Uncompressed AVI');open(video_writer);endh_fig = figure;sz = [790 607]; % figure sizescreensize = get(0,'ScreenSize');xpos = ceil((screensize(3)-sz(1))/2); % center the figure on the screen horizontallyypos = ceil((screensize(4)-sz(2))/2); % center the figure on the screen verticallyset(h_fig, 'Position', [xpos ypos sz])h_3d = subplot(3,3,[1,2,4,5,7,8]);axis equalgrid onview(90,0);ylabel('y [m]'); zlabel('z [m]');quadcolors = lines(1);set(gcf,'Renderer','OpenGL')%% *********************** INITIAL CONDITIONS ***********************t_total = 5; % Total simulated timetstep = 0.01; % this determines the time step at which the solution is givencstep = 0.05; % image capture time intervalmax_iter = t_total/cstep; % max iterationnstep = cstep/tstep;time = 0; % current timeerr = []; % runtime errors% Get start and stop positiondes_start = trajhandle(0,[]);des_stop = trajhandle(inf,[]);% Get boundaryd_state = nan(max_iter,2);for iter = 1:max_iterdd = trajhandle(cstep*iter,[]);d_state(iter,:) = dd.pos(1:2)';endy_lim = [min(d_state(:,1)) - 0.1, max(d_state(:,1)) + 0.1];z_lim = [min(d_state(:,2)) - 0.1, max(d_state(:,2)) + 0.1];if(4*(z_lim(2) - z_lim(1)) < y_lim(2) - y_lim(1))z_lim(1) = z_lim(1) - (y_lim(2) - y_lim(1))/8;z_lim(2) = z_lim(2) + (y_lim(2) - y_lim(1))/8;endstop_pos = des_stop.pos;x0 = [des_start.pos; 0; des_start.vel; 0];xtraj = nan(max_iter*nstep, length(x0));ttraj = nan(max_iter*nstep, 1);x = x0; % statepos_tol = 0.01;vel_tol = 0.02;ang_tol = 0.05;%% ************************* RUN SIMULATION *************************disp('Simulation Running....')% Main loopfor iter = 1:max_itertimeint = time:tstep:time+cstep;tic;% Initialize quad plotif iter == 1subplot(3,3,[1,2,4,5,7,8]);quad_state = simStateToQuadState(x0);QP = QuadPlot(1, quad_state, params.arm_length, 0.05, quadcolors(1,:), max_iter, h_3d);ylim(y_lim); zlim(z_lim);quad_state = simStateToQuadState(x);QP.UpdateQuadPlot(quad_state, time);h_title = title(h_3d, sprintf('iteration: %d, time: %4.2f', iter, time));end% Run simulation[tsave, xsave] = ode45(@(t,s) sys_eom(t, s, controlhandle, trajhandle, params), timeint, x);x = xsave(end, :)';% Save to trajxtraj((iter-1)*nstep+1:iter*nstep,:) = xsave(1:end-1,:);ttraj((iter-1)*nstep+1:iter*nstep) = tsave(1:end-1);% Update quad plotquad_state = simStateToQuadState(x);QP.UpdateQuadPlot(quad_state, time + cstep);subplot(3,3,[1,2,4,5,7,8]);ylim(y_lim); zlim(z_lim);set(h_title, 'String', sprintf('迭代: %d, 时间: %4.2f', iter, time + cstep))time = time + cstep; % Update simulation timeif videowriteVideo(video_writer, getframe(h_fig));endsubplot(3,3,3)plot(ttraj(1:iter*nstep), xtraj(1:iter*nstep,1));xlabel('t [s]'); ylabel('y [m]');grid on;subplot(3,3,6)plot(ttraj(1:iter*nstep), xtraj(1:iter*nstep,2));xlabel('t [s]'); ylabel('z [m]');grid on;subplot(3,3,9)plot(ttraj(1:iter*nstep), 180/pi*xtraj(1:iter*nstep,3));grid on;xlabel('t [s]'); ylabel('\phi [deg]');t = toc;% Check to make sure ode45 is not timing outif(t > cstep*50)err = 'Ode45 Unstable';break;end% Pause to make real-timeif real_time && (t < cstep)pause(cstep - t);end% Check termination criteriaif norm(x(1:2) - stop_pos) < pos_tol && norm(x(4:5)) < vel_tol && abs(x(3)) < ang_tolerr = [];breakenderr = 'Did not reach goal';enddisp('Simulation done');if videoclose(video_writer);endif ~isempty(err)disp(['Error: ', err]);elsedisp(['Final time: ', num2str(time), ' sec']);endt_out = ttraj(1:iter*nstep);s_out = xtraj(1:iter*nstep,:);end
⛳️ 运行结果
 文章来源:https://www.toymoban.com/news/detail-772946.html
文章来源:https://www.toymoban.com/news/detail-772946.html
🔗 参考文献
[1]赵祚喜,施垒,刘雄,等.基于Matlab的水田平地机运动学模型数值解求解[J].农业机械学报, 2015(S1):6.DOI:CNKI:SUN:NYJX.0.2015-S1-011.文章来源地址https://www.toymoban.com/news/detail-772946.html
🎈 部分理论引用网络文献,若有侵权联系博主删除
🎁 关注我领取海量matlab电子书和数学建模资料
👇 私信完整代码、论文复现、期刊合作、论文辅导及科研仿真定制
1 各类智能优化算法改进及应用
生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化
2 机器学习和深度学习方面
卷积神经网络(CNN)、LSTM、支持向量机(SVM)、最小二乘支持向量机(LSSVM)、极限学习机(ELM)、核极限学习机(KELM)、BP、RBF、宽度学习、DBN、RF、RBF、DELM、XGBOOST、TCN实现风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断
2.图像处理方面
图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知
3 路径规划方面
旅行商问题(TSP)、车辆路径问题(VRP、MVRP、CVRP、VRPTW等)、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、车辆协同无人机路径规划、天线线性阵列分布优化、车间布局优化
4 无人机应用方面
无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配、无人机安全通信轨迹在线优化
5 无线传感器定位及布局方面
传感器部署优化、通信协议优化、路由优化、目标定位优化、Dv-Hop定位优化、Leach协议优化、WSN覆盖优化、组播优化、RSSI定位优化
6 信号处理方面
信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化
7 电力系统方面
微电网优化、无功优化、配电网重构、储能配置
8 元胞自动机方面
交通流 人群疏散 病毒扩散 晶体生长
9 雷达方面
卡尔曼滤波跟踪、航迹关联、航迹融合
到了这里,关于【无人机】基于 ode45实现四旋翼无人机姿态仿真附Matlab代码的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!