目录
一.前言
二.算法实现思路
三.算法实现
(1)LSD基数排序
(2)MSD排序
四.算法性能分析和比较
一.前言
基数排序的关键是“多关键词排序
基数排序(Radix Sort)是一种非比较的排序算法,它根据元素的各个位上的值将元素进行排序。它可以分为最低有效位优先(LSD)和最高有效位优先(MSD)两种实现方式。
二.算法实现思路
当使用基数排序时,可以选择使用LSD(最低有效位优先)或MSD(最高有效位优先)算法。下面是它们的算法流程的简要介绍:
LSD(最低有效位优先)算法流程:
- 确定待排序元素的最大位数,假设为d。
- 从最低有效位(个位)开始,依次对元素进行稳定的计数排序(或桶排序),根据当前位的值将元素分配到对应的桶中。
- 按照计数排序的结果,重新排列元素顺序。
- 重复步骤2和3,直到处理完最高有效位(最高位)为止。
- 完成排序后,元素按照从低位到高位的顺序排列,得到有序序列。
MSD(最高有效位优先)算法流程:
- 确定待排序元素的最大位数,假设为d。
- 从最高有效位(最高位)开始,依次对元素进行排序。
- 将元素根据当前位的值分割成多个子序列(桶),每个子序列中的元素具有相同的当前位值。可以使用计数排序、桶排序或递归调用基数排序来对每个子序列进行排序。
- 递归对每个子序列重复步骤2和3,直到处理完最低有效位(最低位)为止。
- 合并所有子序列,得到有序序列。
三.算法实现
我们用java语言对两种排序进行实现
(1)LSD基数排序
从低位到高位排序,我们首先需要获得我们需要排序的位数digitstatic int getNumDigits(int[] num) {//获得最大的数的位数 int max = num[0];//最大的数 int digits = 0;//位数 for (int i = 0; i < num.length; i++) { if (num[i] > max) max = num[i]; } while (max / 10 != 0) { digits++; max = max / 10; } if (max % 10 != 0) { digits++; } return digits; }获得位数后我们从低位到到高位对数字进行分组排序,其中MyQueue为队列结构的类
public static void LSD(int[] num) { //对数字采用最低位优先法排序 MyQueue queue = new MyQueue(10, num.length);//分配10个队列 int digits = getNumDigits(num); int mode = 1; while (digits != 0) { for (int i = 0; i < num.length; i++) { queue.enqueue((num[i] / mode) % 10, num[i]); //按桶分配,(num[i]/mode)%10表示取的位数 } int k = 0; for (int j = 0; j < 10; j++) { while (!queue.isEmpty(j)) { num[k] = (int) queue.dequeue(j); k++; } }//出队 digits--;//位上移 mode = mode * 10; } }这里对于出队部分的代码做进一步的说明
queue.dequeue(j)返回的是一个Object类型的元素,而num数组是一个int类型的数组。因此,在将元素从队列中取出后,需要进行强制类型转换(int),以将其转换为int类型,以便正确地赋值给num数组。由于Java中的泛型不支持基本数据类型,因此在取出元素时,类型会被擦除为Object。出队时一次只会返回一个元素,通过while循环保证队列中所有的元素输出完毕
(输出结果在下面)
下面补充对于长度相等的简单字符串进行LSD排序的例子,对于更加复杂的字符串排序则需要我们针对长度大小/特殊字符的比较进一步判断public static void LSD(String[] str) { //对字符串采取最低位优先法 //对数字采用最低位优先法排序 MyQueue queue = new MyQueue(27, str.length);//分配27个队列 //27个桶,其中第27个桶用来存储除字母以外的其他字符,不区分大小写 int digits = str[0].length();//等长字符的长度 int mode = 1; while (digits != 0) { for (int i = 0; i < str.length; i++) { int index;//桶的下标 if (str[i].charAt(digits - 1) >= 'A' && str[i].charAt(digits - 1) <= 'Z') { index = str[i].charAt(digits - 1) - 'A'; } else if (str[i].charAt(digits - 1) >= 'a' && str[i].charAt(digits - 1) <= 'z') { index = str[i].charAt(digits - 1) - 'a'; } else { index = 26; }//不区分大小写 queue.enqueue(index, str[i]); //按桶分配 } int k = 0; for (int j = 0; j < 27; j++) { while (!queue.isEmpty(j)) { str[k] = (String) queue.dequeue(j); k++; } }//出队 digits--;//位上移 } }
上面代码实现了从低位到高位依次进行排序的代码逻辑,详细的排序过程为:
假设有以下一组整数:[170, 45, 75, 90, 802, 24, 2, 66],我们使用LSD基数排序按照个位数、十位数和百位数进行排序。
首先,按照个位数进行排序,得到:[802, 2, 24, 45, 66, 170, 75, 90]。
然后,按照十位数进行排序,得到:[2, 24, 45, 66, 75, 90, 802, 170]。
最后,按照百位数进行排序,得到:[2, 24, 45, 66, 75, 90, 170, 802]。通过上面的例子我们就可以清晰的看出LSD排序的具体流程
下面是测试函数和输出结果
public static void main(String[] args) { int[] num = {12, 32, 2, 231, 14, 23}; System.out.println("before sorting: " + Arrays.toString(num)); LSD(num); System.out.println("after sorting: " + Arrays.toString(num)); String[] strings = {"abc", "bde", "fad", "abd", "bef", "fdd ", "abe" }; System.out.println("before sorting: " + Arrays.toString(strings)); LSD(strings); System.out.println("after sorting: " + Arrays.toString(strings)); }输出结果为:
before sorting: [12, 32, 2, 231, 14, 23] after sorting: [2, 12, 14, 23, 32, 231] before sorting: [abc, bde, fad, abd, bef, fdd , abe] after sorting: [abc, abd, abe, bde, bef, fad, fdd ]
(2)MSD排序
MSD算法主要采用递归和原地排序的方法,对数组进行原地排序,为了更好的展示排序的不同思路,这里的代码没有采取“新建队列”的方式来表示不同的“桶”,而是直接在数组中划分出不同的区域,来表示不同的“桶”
public class MSD { public static void msdSort(int[] arr) { if (arr == null || arr.length <= 1) { return; } int maxDigit = getNumDigits(arr); // 获取最大位数 msdSort(arr, 0, arr.length - 1, maxDigit); } private static void msdSort(int[] arr, int left, int right, int digit) { if (left >= right || digit <= 0) { return; } int[] count = new int[10]; // 计数数组,用于统计每个桶中元素的个数 int[] temp = new int[right - left + 1]; // 临时数组,用于存储排序后的结果 int div = (int) Math.pow(10, digit - 1); // 用于获取当前位数上的数字 // 统计每个桶中的元素个数 for (int i = left; i <= right; i++) { int num = (arr[i] / div) % 10; count[num]++; } // 计算每个桶中元素在结果数组中的起始位置 int[] startIndex = new int[10]; int prevCount = 0; for (int i = 0; i < 10; i++) { startIndex[i] = prevCount; prevCount += count[i]; } // 将元素按照当前位数分配到对应的桶中 //手动分桶 for (int i = left; i <= right; i++) { int num = (arr[i] / div) % 10; temp[startIndex[num]] = arr[i]; startIndex[num]++; } // 将排序后的结果复制回原数组 System.arraycopy(temp, 0, arr, left, temp.length); // 对每个桶中的元素递归进行排序 for (int i = 0; i < 10; i++) { int bucketLeft = left + startIndex[i] - count[i]; int bucketRight = left + startIndex[i] - 1; msdSort(arr, bucketLeft, bucketRight, digit - 1); } } static int getNumDigits(int[] num) {//略} public static void main(String[] args) { int[] arr = {802, 2, 24, 45, 66, 170, 75, 90}; msdSort(arr); System.out.println(Arrays.toString(arr)); } }
以上是在对int类型进行排序时的代码实现, 将大小比较和Comparable类结合可以实现更多数据类型的排序
四.算法性能分析和比较
LSD VS MSD
1.效率:MSD基数排序在处理大量数据时具有较高的效率。它可以通过递归和分治的方式,对数据进行高效的排序。LSD直接对整个数组中的所有元素进行处理,相对而言效率比较低。
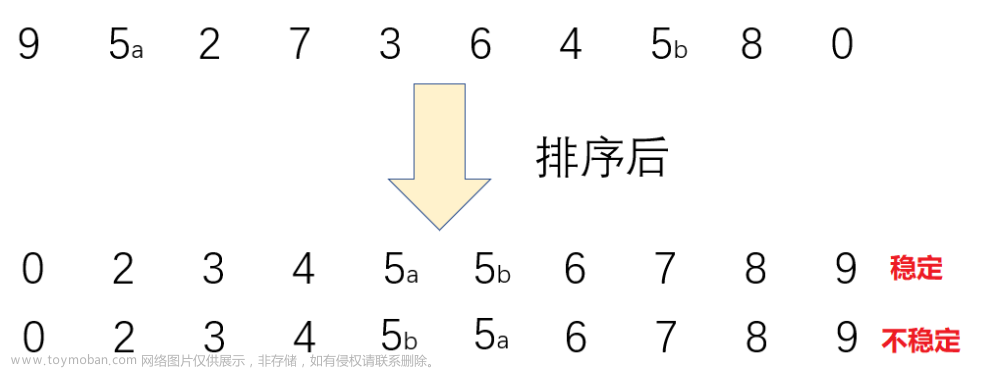
2.稳定性:LSD基数排序是一种稳定的排序算法,相同元素的相对顺序在排序后保持不变,而MSD基数排序在某些情况下可能会造成元素的相对顺序改变,因此它是一种不稳定的排序算法。
3.适用性:MSD:MSD基数排序适用于处理大范围的数据,特别是当数据具有不均匀分布的情况下。它在处理字符串排序时也很常用。LSD基数排序适用于处理数字范围较小且长度相同的数据,例如固定长度的整数。它在处理大量数字排序时具有较好的性能。文章来源:https://www.toymoban.com/news/detail-772955.html
对MSD的不稳定做进一步的说明,如果全程只是用MSD算法,那么算法是稳定的,但是在任务执行过程中,对于每个子桶中的递归和排序我们可能引入更加高效的算法来提升效率,在这个过程中可能会使用一些不稳定的算法。 文章来源地址https://www.toymoban.com/news/detail-772955.html
到了这里,关于基数排序MSD和LSD实现和比较的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!