【栈与队列】之栈的顺序存储（图文详细介绍！！）-Toy模板网

这篇具有很好参考价值的文章主要介绍了【栈与队列】之栈的顺序存储（图文详细介绍！！）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

前言：本章基于《大话数据结构》和王卓老师的视频内容，为刚接触数据结构的初学者提供一些帮助。

💕如果我的文章对你有帮助，点赞、收藏、留言都是对我最大的动力

4.1 栈的定义

4.2 栈的抽象数据类型

4.3 栈的顺序存储结构及实现

4.4 完整代码

4.1 栈的定义

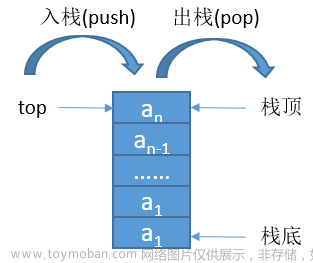
栈：是限定仅在表尾进行插入和删除操作的线性表

允许插入和删除的一端称为栈顶，另一端称为栈底。

空栈：不包含任何数据元素的栈称为空栈。

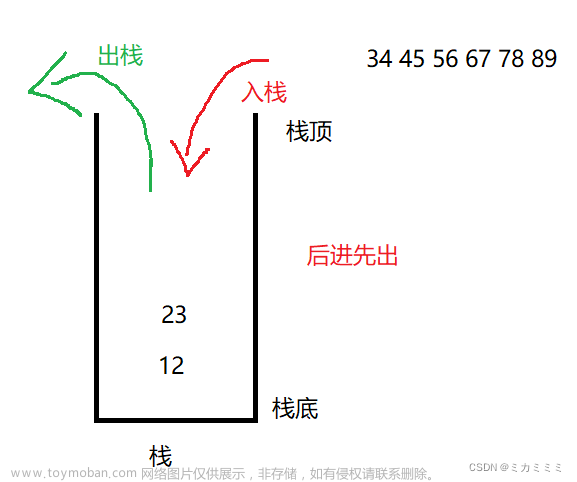
栈又称为后进先出的线性表，简称LIFO结构。

进栈（插入操作）：也称为压栈、入栈。

出栈（删除操作）：也叫做弹栈。

栈的入栈和出栈的顺序规律,第四章栈和队列,数据结构,链表

举例：有三个整数1、2、 3依次进栈，会出现几种出栈次序呢？

第一种：1、2、3进，再3 、2、 1出
第二种: 1进, 1出 ,2进, 2出, 3进，3出。也就是进一个就出一个,出栈为1、2、3。
第三种: 1进, 2进, 2出，1出, 3进，3出。出栈次序为2、1、3。
第四种:1进，1出，2进,3进，3出，2出。出栈次序为1、3、2。
第五种:1进, 2进, 2出，3进，3出,1出。出栈次序为2、3、1。

栈与一般线性表的异同：

	一般线性表	栈
逻辑结构	一对一	一对一
存储结构	顺序表、链表	顺序栈、链栈
运算规则	随机存取	后进先出

4.2 栈的抽象数据类型

ADT Stack{

数据对象：D={|属于Elemset,(i=1,2,3...,n,n0}

数据关系：R={<,>|,,属于D，（i=2,3,...,n）}

约定an端为栈顶，a1端为栈底。

基本操作：初始化、进栈、出栈、取栈顶元素等

}ADT Stack

4.3 栈的顺序存储结构及实现

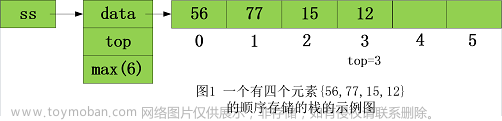
存储方式：同一般线性表的顺序存储结构完全相同，利用一组地址连续的存储单元依次存放自栈底到栈顶的数据元素。栈底一般在低地址端。

top指针，指示栈顶元素在顺序栈中的位置。 base指针，指示栈底元素在顺序栈中的位置。

stacksize表示栈可使用的最大容量。

栈的入栈和出栈的顺序规律,第四章栈和队列,数据结构,链表

栈的结构定义：

#define MAXSIZE 100
typedef struct{
    SElemType *base;//SElemType是自定义类型，base是栈底指针
    SElemType *top;//top是栈顶指针
    int stacksize;//栈可用最大容量
}SqStack;

顺序栈的初始化：

Status lnitStack(SqStack& S)//这里的S不是结构体指针所以下面可以不用S->
{
	S.base = (SElemType*)malloc(MAXSIZE*sizeof(SElemType));//动态分配
	//S.base = new SElemType[MAXSIZE];//C++的分配，这里其实是指向数组的首元素的地址
	
	if (!S.base)
		exit(OVERFLOW);//存储失败
	S.top = S.base;//栈顶指针等于栈底指针
	S.stacksize = MAXSIZE;
	return OK;
}

判断顺序栈是否为空：

算法分析：栈为空的话，top指针==base指针

栈的入栈和出栈的顺序规律,第四章栈和队列,数据结构,链表

Status StackEmpty(SqStack S)
{
	if (S.top = S.base)//如果栈顶和栈底相等，则为空
		return TRUE;
	else
		return FALSE;
}

求顺序栈的长度：

算法分析：S.stacksize=S.top-S.base

栈的入栈和出栈的顺序规律,第四章栈和队列,数据结构,链表

int StackLength(SqStack S)
{
	return S.top - S.base;
}

清空顺序栈：

Status ClearStack(SqStack S)
{
	if (S.base)S.top = S.base;//base存在这样一个地址，则top指针下移
	return OK;
}

销毁顺序栈：

Status DestroyStack(SqStack& S)
{
	if (S.base)
	{
		delete S.base;//我们在删除一个指针之后，编译器只会释放该指针所指向的内存空间，而不会删除这个指针本身。
		//free(S.base);
		S.stacksize = 0;
		S.base = S.top = NULL;//不设置为空，则成为野指针
	}
	return OK;
}

顺序栈的入栈：

算法分析：

判断是否栈满，若满则出错（上溢）
元素e压入栈顶
栈顶指针加1

栈的入栈和出栈的顺序规律,第四章栈和队列,数据结构,链表

Status Push(SqStack& S, SElemType e)
{
	if (S.top - S.base == S.stacksize)//栈满
		return ERROR;
	*S.top++ = e;//取值，然后给他赋值，然后S.top++
	return OK;
}

顺序栈的出栈：

算法分析：

判断是否栈空，若满则出错（上溢）
获取栈顶元素e
栈顶指针减1

栈的入栈和出栈的顺序规律,第四章栈和队列,数据结构,链表文章来源地址https://www.toymoban.com/news/detail-773338.html

Status Pop(SqStack& S, SElemType& e)//若栈不空，则删除S的栈顶元素，用e返回其值，并返回OK
{
	if (S.top == S.base)//等价于if(StackEmpty(S))
		return ERROR;
	e = *--S.top;//相当与--S.top; e=*S.top
	return OK;
}

4.4 完整代码

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>

#include <malloc.h>
#define MAXSIZE 100
#define OK 1
#define TRUE 1
#define FALSE 0
#define OVERFLOW -2
#define ERROR 0
typedef int  SElemType;
typedef int Status;

//顺序栈的初始化
typedef struct
{
	SElemType* base;//栈底指针
	SElemType* top;//栈顶指针
	int stacksize;//栈可用最大容量
}SqStack;
Status lnitStack(SqStack& S)//这里的S不是结构体指针所以下面可以不用S->
{
	S.base = (SElemType*)malloc(MAXSIZE*sizeof(SElemType));//动态分配
	//S.base = new SElemType[MAXSIZE];//C++的分配，这里其实是指向数组的首元素的地址
	
	if (!S.base)
		exit(OVERFLOW);//存储失败
	S.top = S.base;//栈顶指针等于栈底指针
	S.stacksize = MAXSIZE;
	return OK;
}
//顺序栈判断栈是否为空
Status StackEmpty(SqStack S)
{
	if (S.top = S.base)//如果栈顶和栈底相等，则为空
		return TRUE;
	else
		return FALSE;
}
//求顺序栈的长度
int StackLength(SqStack S)
{
	return S.top - S.base;
}
//清空顺序栈
Status ClearStack(SqStack& S)
{
	if (S.base)
		S.top = S.base;//base存在这样一个地址，则top指针下移
	return OK;
}
//销毁顺序栈
Status DestroyStack(SqStack& S)
{
	if (S.base)
	{
		delete S.base;//我们在删除一个指针之后，编译器只会释放该指针所指向的内存空间，而不会删除这个指针本身。
		//free(S.base);
		S.stacksize = 0;
		S.base = S.top = NULL;//不设置为空，则成为野指针
	}
	return OK;
}

//顺序栈的入栈
Status Push(SqStack& S, SElemType e)
{
	if (S.top - S.base == S.stacksize)//栈满
		return ERROR;
	*S.top++ = e;//取值，然后给他赋值，然后S.top++
	return OK;
}

//顺序栈的出栈
Status Pop(SqStack& S, SElemType& e)//若栈不空，则删除S的栈顶元素，用e返回其值，并返回OK
{
	if (S.top == S.base)//等价于if(StackEmpty(S))
		return ERROR;
	e = *--S.top;
	return OK;
}
//顺序栈的遍历
Status printList(SqStack S)
{
	SElemType* p;

	if (S.top == S.base) {
		printf("Stack is NULL.\n");
		return 0;
	}
	p = S.top;
	// 由栈顶依次向下遍历
	while (p > S.base) {
		p--;
		printf("%d ", *p);
	}
	printf("\n");
	return 1;

}
int main()
{
	SqStack S;
	SElemType e,n,i;
	lnitStack(S);//初始化
	printf("input the length of the Stack :\n");
	scanf("%d", &n);
	for (i = 1; i <= n; i++) {
		scanf("%d", &e);
		Push(S, e);//入栈
	}
	printList(S);//遍历
	printf("长度为：%d\n",StackLength(S));
	ClearStack(S);//清空栈
	printList(S);
	printf("长度为：%d\n", StackLength(S));
	DestroyStack(S);//销毁栈
	printList(S);
	printf("长度为：%d", StackLength(S));

}

到了这里，关于【栈与队列】之栈的顺序存储（图文详细介绍！！）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！