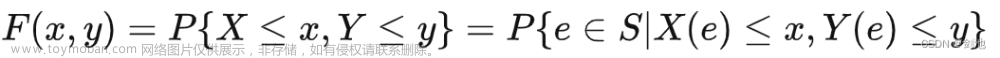深度学习-必备的数学知识-概率论3-Toy模板网

这篇具有很好参考价值的文章主要介绍了深度学习-必备的数学知识-概率论3。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

深度学习

必备的数学知识

概率论

我们将接着上一篇文章继续讲解。

条件概率

大家还记得上一篇文章的提到的联合概率分布吗？定义在一组变量的联合概率分布的子集上的概率分布被称为边缘概率分布（marginal probability distribution）。
对于离散型随机变量x和y，如果我们有 $P (x, y)$ ,则可以根据以下求和法则（sum rule）来计算 $P (x)$
$\forall x \in x,P(x=x)=\sum_{y}P(x=x,y=y)$
例如，假设我们有两个离散随机变量 $x$ 和 $y$ ，它们的可能值分别为 $x = {1, 2}$ 和 $y = {a, b}$ 。假设我们知道以下联合概率：

$P (x = 1, y = a) = 0.1$
$P (x = 1, y = b) = 0.2$
$P (x = 2, y = a) = 0.3$
$P (x = 2, y = b) = 0.4$
那么我们可以通过对所有可能的 $y$ 值求和来计算 $x$ 取特定值的概率：
$P (x = 1) = P (x = 1, y = a) + P (x = 1, y = b) = 0.1 + 0.2 = 0.3$
$P (x = 2) = P (x = 2, y = a) + P (x = 2, y = b) = 0.3 + 0.4 = 0.7$

这就是如何使用这个公式来计算概率的一个例子。
对于连续性随机变量，通过对联合概率求积分来计算 $P (x)$
$P(x)=\int P(x,y)dy$

条件概率

条件概率指的是某件事在给定的其他事件发生时出现的概率。我们将当x=x时，y=y发生的概率记作 $P (y = y ∣ x = x)$ 。条件概率可以通过以下公式计算
$P(y=y|x=x)=\frac{P(y=y,x=x)}{P(x=x)}$
需要注意的是，条件概率只有在 $P (x = x) > 0$ 时才有定义，也就是说，我们不能计算在某个肯定不会发生的事件的条件下另一事件发生的概率

注意条件概率说的不是某件事发生后会发生什么。假定一个人拿着车钥匙出门，那么他开车的概率很高，但是让一个人拿车钥匙他的出行方式不会改变。

条件概率的链式法则

概率的链式法则（chain rule）（也称为乘法法则）是一种用于计算多个随机变量的联合概率的方法。对于两个随机变量 $x$ 和 $y$ ，链式法则可以写作：

$\cdot P(y=y|x=x)$

这个公式表示 $x = x$ 和 $y = y$ 同时发生的概率等于 $x = x$ 发生的概率乘以在 $x = x$ 的条件下 $y = y$ 发生的概率。

相信大家已经看出来了，这是从关系概率的公式推导而来的。
$P(y=y|x=x)=\frac{P(y=y,x=x)}{P(x=x)}\\ P(x=x) \cdot P(y=y|x=x)=\frac{P(y=y,x=x)}{P(x=x)} \cdot P(x=x)\\ P(y=y,x=x)= P(x=x) \cdot P(y=y|x=x)$

链式法则可以扩展到更多的随机变量
$P(x^{(1)},x^{(2)},...,x^{(n)})=P(x^{1})\prod^{n}_{i}P(x^{(i)}|x^{1},...,x^{(i-1)})$

独立性和条件独立性

我们称两个随机变量相互独立的（independent），这意味着它的联合概率分布等于它们各自的概率分布的乘积,知道 $x$ 的值并不会改变 $y$ 的概率分布，反之亦然。
$\forall x \in x,y \in y P(x=x,y=y)=P(x=x) \cdot P(y=y)$

如果在给定随机变量z=z的条件下，随机变量x和y是独立的，我们就说x和y在z=z的条件下是条件独立的conditionally independent）。换句话说，对于x和y的条件概率分布对于z的每一个值都可以写成乘积的形式。用公式表示为：
$\forall x \in X, y \in Y, z \in Z, P(X=x, Y=y|Z=z) = P(X=x|Z=z) \cdot P(Y=y|Z=z)$ 文章来源地址https://www.toymoban.com/news/detail-773354.html