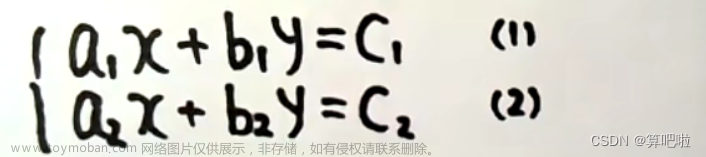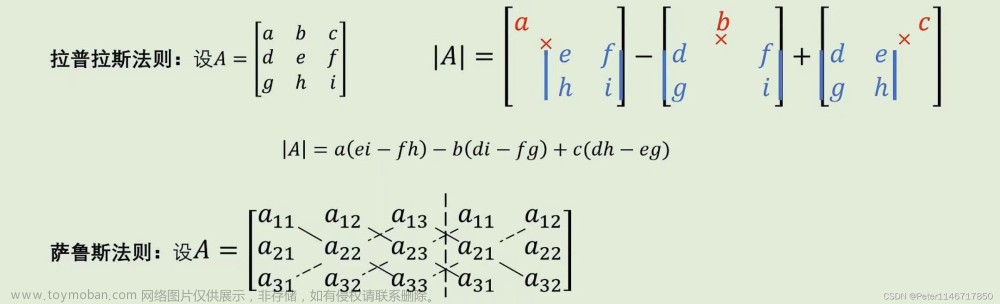计算机视觉一些算法中常会用到线性代数的一些知识,为了便于理解和快速回忆,博主这边对常用的一些知识点做下整理,主要来源于如下这本书籍。

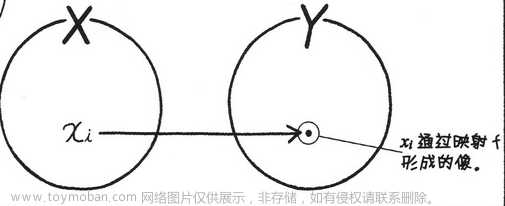
1. 矩阵不仅仅是数字排列而已,不然也不会有那么大精力研究它。其可以表示一种映射

关于映射,变换的一些帖子可以参考如下的
仿射变换(AffineTransform)与仿射矩阵-CSDN博客
图像的仿射变换 - 知乎
https://www.cnblogs.com/bnuvincent/p/6691189.html
2. 矩阵即是映射



3. 矩阵的运算



4.矩阵的逆

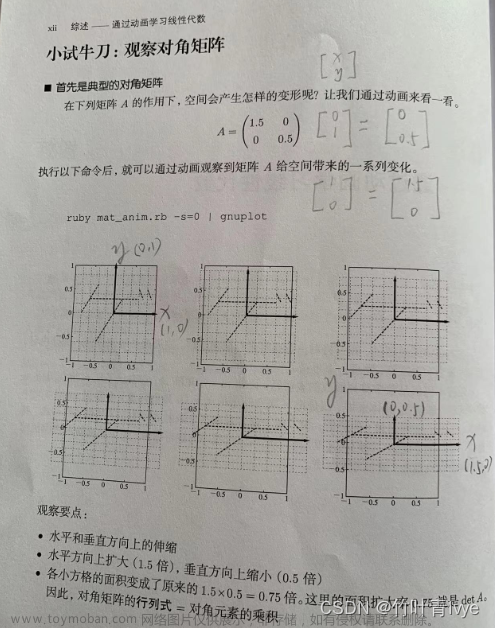
5.行列式



.
行列式计算也可参考其它帖子
行列式10种计算方法!几何及线代必考知识点梳理! - 知乎
线性代数行列式知识点总结


线代学习笔记(7)- 行列式 - 知乎
6. 逆矩阵的计算
求逆矩阵的三种方法
计算逆矩阵的三种方法_矩阵求逆公式-CSDN博客


7. 初等变换
矩阵的初等变换 - 知乎
百度安全验证

8. 线性方程组的解


高斯-若尔当消元法_百度百科

线性代数的学习和整理14: 线性方程组求解的3种方法,重点讲矩阵函数求解-CSDN博客
矩阵基础4-线性方程组详解 - 简书
齐次线性方程组_百度百科
https://jingyan.baidu.com/article/fec7a1e5cb631f1190b4e732.html
线代-3.非齐次线性方程组解法 - 知乎
齐次和非齐次线性方程组的解法(整理定稿)
9. 单射,满设,双射



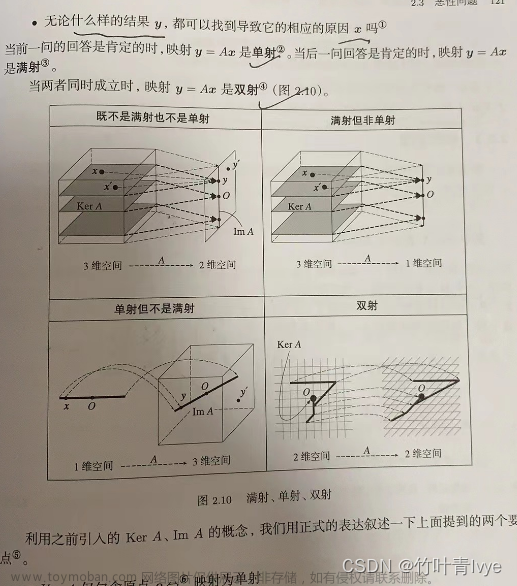
10. 矩阵的秩
一些关于矩阵秩的总结 - 知乎
DAY46|线代『矩阵』核心考点:矩阵的秩
如何理解矩阵的「秩」?
解的关系所确定的系数矩阵秩的关系 - 知乎
11.2 齐次线性方程组的基础解系和通解 - 知乎
11. 特征值和特征向量









线性代数的本质(10)-特征值与特征向量 - 知乎
11.3 求解特征值和特征向量(基础解系法) - 知乎
12. 矩阵对角化
12.2 对称矩阵的正交对角化 - 知乎
什么样的矩阵可以对角化? - 知乎
对角化_百度百科
13. 相似性矩阵
相似矩阵_百度百科
怎么证明两个矩阵相似? - 知乎
百度安全验证
如何证两矩阵相似 - 知乎
“拨开迷雾”,如何判定矩阵相似? - 知乎
线性代数(相似矩阵) - 知乎
14. Jordan标准型
矩阵分析:特征值,相似度对角化,Jordan标准形_jordan标准型和特征值的关系-CSDN博客
Jordan标准型_百度百科
15. 正定矩阵
浅谈「正定矩阵」和「半正定矩阵」
矩阵理论| 特殊矩阵:正定矩阵-CSDN博客
MIT—微分方程与线性代数笔记7.2 正定矩阵 - 知乎
·16.正交矩阵
14、范数、内积、归一、正交化、标准正交(Schmidt化) - 知乎
线性代数(正交矩阵) - 知乎
线性代数(正交矩阵) - 知乎
正交规范化、正交矩阵_矩阵正交规范化-CSDN博客
如何理解施密特(Schmidt)正交化 - 知乎
正交矩阵的几何意义是什么? - 知乎
17.矩阵和坐标系变换的关系
浅谈矩阵乘法与坐标系变换 - 知乎
一些关于矩阵秩的总结 - 知乎’
矩阵与坐标系的映射关系_矩阵坐标-CSDN博客
矩阵变换坐标系 深入理解 - 知乎
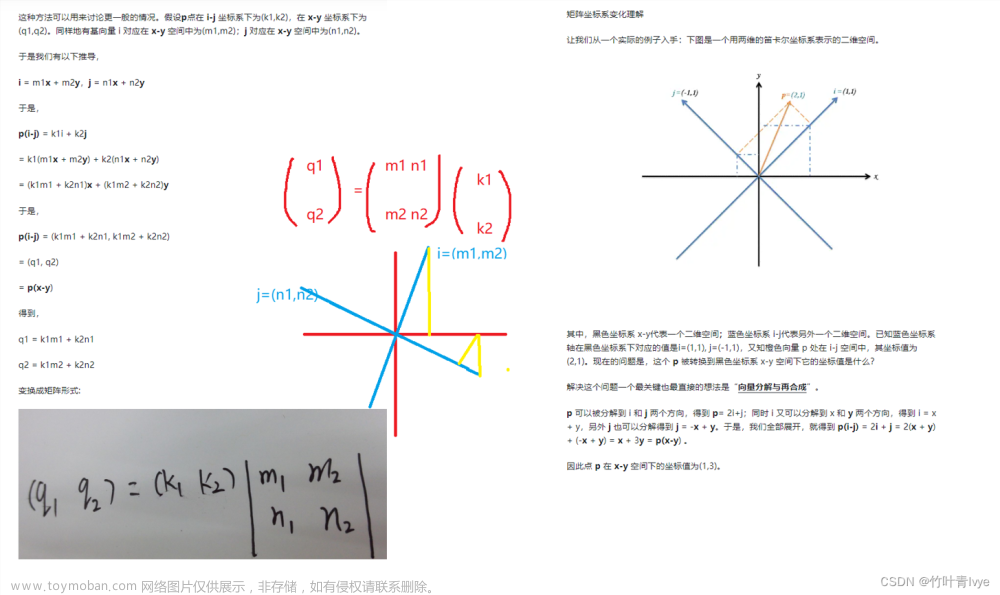
(m1,n1) 可以表示x轴在i-j坐标系下的坐标;(m2,n2)可以表示y轴在i-j坐标系下的坐标。然后又知道点在i-j下的坐标,便可以直接投影。
补充:已知一个点p的坐标(在A坐标系),去求此点在另一个坐标系B中的坐标q,博主推断出了一种方法:
1. 求坐标系B的两个轴在A坐标系下的坐标向量表示。
2. 然后将点p坐标向量和上面的两个坐标向量各做内积,就能得到新坐标系下的坐标q位置。下图中是构造了一个矩阵,矩阵之前也提到过,矩阵乘积可看成是在做变换,也可以看成是点在此矩阵的每一行所构造的轴上的投影。


线性代数(三):坐标变换 - 知乎
18.奇异值分解
SVD-矩阵奇异值分解 —— 原理与几何意义 - 知乎
百度安全验证
奇异值分解(SVD)原理总结
《统计学习方法》之SVD - 知乎
基础算法-奇异值分解SVD_右奇异向量-CSDN博客
线性代数的本质(10)-特征值与特征向量 - 知乎
19.常见矩阵
线性代数导学(八): 那些常见且特殊的矩阵与其目的 - 知乎
20.LU分解
LU分解 - 知乎
lu分解有什么意义啊? - 知乎
补充知识点:
21. 微分方程
微分方程的求解方法_微分方程求解方法总结-CSDN博客
求解微分方程
常(偏)微分方程的数值求解(欧拉法、改进欧拉法、龙格-库塔法、亚当姆斯法) - 知乎
总归想办法两边换成dy,dx各自积分的形式
高数技巧 | 重要的一元积分公式总结 - 知乎
高等数学 | 考研数学 | 微分方程总结 - 知乎
百度安全验证
22. 左手和右手坐标系
左手坐标系和右手坐标系_左手坐标系和右手坐标系的区别-CSDN博客
左手坐标系 右手坐标系 区别 - 知乎
23. roll, pitch, yaw文章来源:https://www.toymoban.com/news/detail-773672.html
pitch yaw roll是什么_yaw pitch roll-CSDN博客文章来源地址https://www.toymoban.com/news/detail-773672.html
到了这里,关于线性代数基础知识的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!