图(Graph)G由两个集合V和E组成,记为G=(V, E),其中V是顶点的有穷非空集合,E是V中顶点偶对的有穷集合,这些顶点偶对称为边。V(G)和E(G)通常分别表示图G的顶点集合和边集合,E(G)可以为空集。若EG)为空,则图G只有顶点而没有边。
子图:假设有两个图G=(V,E)和G1=(V1,E1);如果V1V,E1E,则称G1为G的子图。
完全图:任意两个顶点都有一条边相连。(指的是无向图)
无向完全图和有向完全图:对于无向图,若具有n(n-1)/2条边,则称为无向完全图;对于有向图,若具有n(n-1)条弧,则称为有向完全图。
稀疏图和稠密图:有很少条边或弧(如e<nlogn)的图称为稀疏图,反之称为稠密图
权和网:在实际应用中,每条边可以标上具有某种含义的数值,该数值称为该边上的权,这些权可以表示从一个顶点到另一个顶点的距离或耗费。这种带权的图通常称为网。
邻接点:对于无向图G,如果图的边(v, v1)E,则称顶点v和v1互为邻接点,即v和v1相邻接。
关联(依附):边/弧与顶点之间的关系;边(v, v')依附于顶点v和v1,或者说边(v, v1)与顶点v和v1相关联。
顶点的度:与该顶点相关联的边的数目,记为TD(v);在有向图中,顶点的度等于该顶点的入度与出度之和,顶点v的入度是以v为终点的有向边的条数,记作ID(v),顶点的出度是以v为始点的有向边的条数,记作OD(v)。
路径:接续的边构成的顶点序列
路径长度:路径上边或弧的数目/权值之和
回路(环):第一个顶点和最后一个顶点相同的路径
简单路径:除路径起点和终点可以相同外,其余顶点均不相同的路径
简单回路(简单环):除路径起点和终点相同外,其余顶点均不相同的路径。
连通:两个顶点之间有路径,则称这两个顶点是连通的。
连通图:对于图中任意两个顶点都是连通的,则称该图是连通图
强连通图:在有向图中对于任意两个顶点是连通的,则称该图是强连通图。
连通分量:指的是无向图中的极大连通子图(极大连通子图意思为该子图是G的连通子图,将G的任何不在该子图中的顶点加入,子图不再连通)
强连通分量:有向图的极大强连通子图
极小连通子图:该子图是G的连通子图,在该子图中删除任何一条边子图不再连通
连通图的生成树:包含无向图所有顶点的极小连通子图
有向树:有一个顶点的入度为0,其余顶点的入度均为1的有向图称为有向树
生成森林:对于非连通图,由各个连通分量的生成树的集合
图的基本概念:
1、有向图
若E是有向边(也称弧)的有限集合时,则图G为有向图。弧是顶点的有序对,记为<v, w>,其中v,w是顶点,v称为弧尾,w称为弧头,<v,w>称为从顶点v到顶点w的弧,也称v邻接到w,或w邻接自v。

图(a)所示的有向图G可表示为:

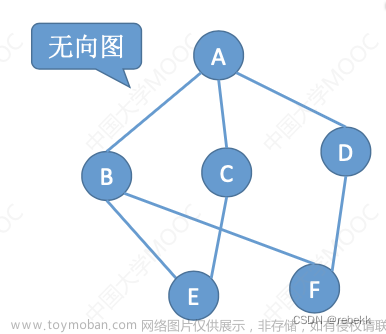
2、无向图
若E是无向边(简称边)的有限集合时,则图G为无向图。边是顶点的无序对,记为(v, w)或(w,v),因为(v,w)=(w,v), 其中v,w是顶点。可以说顶点w和顶点v互为邻接点。边(v, w)依附于顶点w和v,或者说边(v, w)和顶点v, w相关联。
图(b)所示的无向图G2可表示为:
无向图是对称的
3、完全图(也称简单完全图)
对于无向图,∣E∣的取值范围是0 到n ( n − 1 ) / 2 ,有n ( n − 1 ) / 2 条边的无向图称为完全图,在完全图中任意两个顶点之间都存在边。对于有向图,∣E∣的取值范围是0 到n ( n − 1 ) ,有n ( n − 1 ) 条弧的有向图称为有向完全图,在有向完全图中任意两个顶点之间都存在方向相反的两条弧。
4、稠密图、稀疏图
边数很少的图称为稀疏图,反之称为稠密图。稀疏和稠密本身是模糊的概念,稀疏图和稠密图常常是相对而言的。一般当图G满足∣ E ∣ < ∣ V ∣ l o g ∣ V时,可以将G 视为稀疏图。
5、子图
设有两个图G = ( V , E ) 和G ′ = ( V ′ , E ′ ) ,若V '是V 的子集,且E ′ 是E 的子集,则称G ′ G的子图。
6、出度、入度
出度:以尾为弧
入度:以头为弧
对于无向图,顶点v的度是指依附于该顶点的边的条数,记为T D ( v )。在具有n 个顶点、e 条边的无向图中,
7、回路或环
第一个顶点和最后一个顶点相同
8、连通图
图中任意两顶点连通,则这个图为连通图(它是无向图)
9、非连通图
如果一个图有n个顶点和小于n-1条边,就是非连通图
10、生成树
连通图的生成树是包含图中全部顶点的一个极小连通子图。若图中顶点数为n ,则它的生成树含有n − 1 条边(无向图)
11、生成森林
一个有向图恰有一个顶点的入度为0,其余顶点的入度均为1,则是一颗有向树。生成森林由多个有向树组成。
图的存储结构:
数组表示法:
用两个数组分别存储数据元素(顶点)的信息和数据元素之间的关系(边或弧)
其中图用0或1来表示,网用权或者∞来表示
网的邻接矩阵:
定义:
若<>或()
∞ 反之
图的邻接表特点:有e条边就会有2e个1对称,即:
邻接表:
邻接表是一种常用的图的数据结构,用于表示图中顶点之间的关系。它通过使用链表来存储每个顶点的邻接点。
在邻接表中,图的顶点被表示为一个数组,数组的每个元素都是一个链表。链表中的每个节点表示一个邻接点,节点中存储了与该顶点相邻的顶点的信息。
连接点域:指示与定点邻接的点在图中位置(下标)
链域:下一条边或弧的结点
数据域:数据域存储和边或弧相关的信息,如权值
头结点
| data数据 | firstarc(指针) |
表结点
| adjvex | nextarc | info |
若无向图中有n个顶点,e条边,则它的邻接表需n个头结点和2e个表结点
若有向图中有n个顶点,e条边,则它的邻接表需n个头结点和e个表结点
图的遍历(相当于树):
深度优先搜索类似于树的先序遍历(广度=层次)。如其名称中所暗含的意思一样,这种搜索算法所遵循的搜索策略是尽可能“深”地搜索一个图。它的基本思想如下:首先访问图中某一起始顶点v,然后由v出发,访问与v邻接且未被访问的任一顶点再访问与邻接且未被访问的任一顶点…重复上述过程。当不能再继续向下访问时,依次退回到最近被访问的顶点,若它还有邻接顶点未被访问过,则从该点开始继续上述搜索过程,直至图中所有顶点均被访问过为止。
图的连通性:
最小生成树:
一颗生成树就的代价就是树上各代价之和。对于一个带权连通无向图G = ( V , E ) ,生成树不同,其中边的权值之和最小的那棵生成树(构造连通网的最小代价生成树),称为G的最小生成树。
克鲁斯卡尔算法:
构造最小生成树的过程如下图所示。初始时为只有n个顶点而无边的非连通图T = V ,每个顶点自成一个连通分量,然后按照边的权值由小到大的顺序,不断选取当前未被选取过且权值最小的边,若该边依附的顶点落在T中不同的连通分量上,则将此边加入T ,否则舍弃此边而选择下一条权值最小的边。以此类推,直至T 中所有顶点都在一个连通分量上。

我们将下面左图的邻接矩阵通过程序转化为右图的边集数组,并且对它们按权值从小到大排序

拓扑排序
对一个AOV网进行拓扑排序的算法有很多,下面介绍比较常用的一种方法的步骤:文章来源:https://www.toymoban.com/news/detail-773754.html
①从AOV网中选择一个没有前驱的顶点并输出。
②从网中删除该顶点和所有以它为起点的有向边。
③重复①和②直到当前的AOV网为空或当前网中不存在无前驱的顶点为止。如果输出顶点数少了,哪怕是少了一个,也说明这个网存在环(回路),不是AOV网。 文章来源地址https://www.toymoban.com/news/detail-773754.html
文章来源地址https://www.toymoban.com/news/detail-773754.html
到了这里,关于数据结构第七章的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!




![[JavaScript] 第七章 对象](https://imgs.yssmx.com/Uploads/2024/02/785560-1.jpeg)