这篇具有很好参考价值的文章主要介绍了鞍点的判断（黑森矩阵/黑塞矩阵）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。
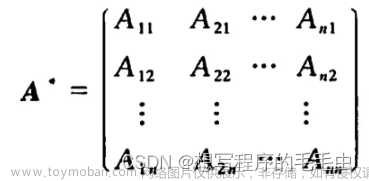
判断鞍点的一个充分条件是：函数在一阶导数为零处（驻点）的黑塞矩阵为不定矩阵。
半正定矩阵： 所有特征值为非负。
半负定矩阵：所有特征值为非正。
不定矩阵：特征值有正有负。
容易解出特征值一个为2,一个为-2（有正有负），显然是不定矩阵，
注意：函数在一阶导数为零处（驻点）的黑塞矩阵为不定矩阵只是判断该点是否为鞍点的充分条件，也就是说函数在一阶导数为零处（驻点）的黑塞矩阵不满足不定矩阵的定义，也不一定能够说明它不是鞍点。
比如在 z=x^4−y^4 点 (0,0)处的 Hessian 矩阵是一个 0 矩阵,并不满足是不定矩阵，但是它是一个鞍点文章来源：https://www.toymoban.com/news/detail-774027.html
所以该点是鞍点！文章来源地址https://www.toymoban.com/news/detail-774027.html
到了这里，关于鞍点的判断（黑森矩阵/黑塞矩阵）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！
雅可比矩阵，Jacobi matrix 或者 Jacobian，是 向量值函数 （ f : R n → R m f:mathbb{R}^n to mathbb{R}^m f : R n → R m ）的一阶偏导数按行排列所得的矩阵。 黑塞矩阵，又叫海森矩阵，Hesse matrix，是 多元函数 （ f : R n → R f:mathbb{R}^n to mathbb{R} f : R n → R ）的二阶偏导数组成的方阵。
1 同济大学高等数学定义 2 国际上的定义 3 黑塞矩阵 我们从几何上看到，在有的曲线弧上，如果任取两点，则联结这两点间的弦总位于这两点间的弧段的上方，如图3-8（a）；而有的曲线弧，则正好相反，如图 3-8（b）。曲线的这种性质就是曲线的凹凸性。 因此曲线的凹凸性可
最近看论文，发现论文中有通过黑塞(Hessian)矩阵提高电驱系统稳定性的应用。所以本篇主要从Hessian矩阵的性质出发，对其中正定矩阵的判定所引发的想法进行记录。 (其实看论文出现黑塞很惊奇，因为前不久刚读了作家黑塞的《德米安：彷徨少年时》，所以在这一领域的黑塞
雅可比矩阵和行列式（Jacobian）_雅可比行列式_JasonKQLin的博客-CSDN博客 在牛顿迭代法、L-M中求解非线性方程组，都会用到雅可比(一阶偏导数) 和黑塞矩阵（2阶偏导数）矩阵。 雅可比矩阵 是一阶偏导数以一定方式排列成的矩阵, 其行列式称为雅可比行列式。 是一个从欧
给定一个 n×m 的整数矩阵，行的编号为 1∼n，列的编号为 1∼m，求矩阵中的所有鞍点。 鞍点，即该位置上的元素在该行上最大，在该列上最小。 有可能有多个鞍点，也可能没有鞍点。 输入格式 第一行包含两个整数 n,m。 接下来 n行，每行包含 m 个整数。 输出格式 输出
输入样例： 输出样例：
遍历数组，将数组内的元素与ma x进行对比并储存最大值和坐标值。 列的实现与行的类似 打印鞍点及其坐标
找鞍点 分数 14 作者 C课程组 单位 浙江大学 一个矩阵元素的“鞍点”是指该位置上的元素值在该行上最大、在该列上最小。 本题要求编写程序，求一个给定的n阶方阵的鞍点。 输入格式： 输入第一行给出一个正整数n（1≤n≤6）。随后n行，每行给出n个整
1. 平移 （Translation） 在2D空间中，我们经常需要将一个点平移到另一个位置。假设空间中的一点 P ( x , y ) P(x,y) P ( x , y ) ；将其向 x , y x, y x , y 方向分别平移 t x t_x t x ， t y t_y t y , 假设平移后点的坐标为 ( x ′ , y ′ ) (x\\\',y\\\') ( x ′ , y ′ ) ,则上述点的平移操作可以归纳为
A 为一个n阶矩阵，行列式 | A | 的每个元素a ij 的代数余子式Aij组成的矩阵叫做伴随矩阵，记作 A* ； a. 如果 A 矩阵可逆，A* = | A | A^-1 b. | A | = | A |^(n-1) c. ( kA )* = k^(n-1) A* a. 若矩阵的行列式结果值不等于 0 ，那么这个矩阵就是
