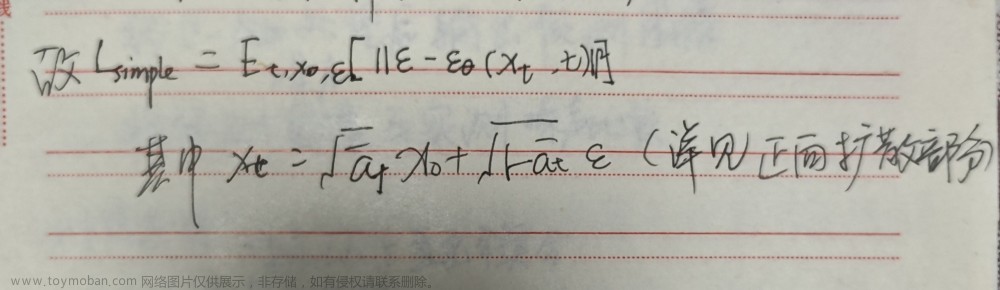Diffusion&Stable Diffusion扩散模型与稳定扩散模型
摘要
本篇文章为阅读笔记，，主要内容围绕扩散模型和稳定扩散模型展开，介绍了kl loss、vae模型的损失函数以及变分下限作为扩展部分。扩散模型是一种生成模型，定义了一个逐渐扩散的马尔科夫链，逐渐项数据添加噪声，然后学习逆扩散过程，从噪声中构建所需的数据样本。稳定扩散模型在其基础上添加了编码器用以降维训练数据、降低训练成本，该模型亦添加了额外的文本嵌入向量，通过该向量模型得以根据文本生成图片。
主要内容参考deephub,“Diffusion 和Stable Diffusion的数学和工作原理详细解释”,https://zhuanlan.zhihu.com/p/597924053
Abstract
This article is a reading note, the main content is around the diffusion model and stable diffusion model, and introduces the loss function of VAE model, KL loss and the variational lower bound as an extended part. Diffusion model is a generative model that defines a progressively diffused Markov chain, gradually adding noise to the data, and then learning the reverse diffusion process to construct the required data samples from the noise. On the basis of this, an encoder is added to the stable diffusion model to reduce the dimensionality of the training data data and reduce the training cost. The model also adds an additional text embedding vector, through which images can be generated from the text.
Diffusion Model扩散模型
训练
- 正向扩散 → \rightarrow →在图中添加噪声
- 反向扩散 → \rightarrow →去除图中噪声
Forward Diffusion Process正向扩散过程
噪声图像的分布
q ( x t ∣ x t − 1 ) = N ( x t ; 1 − β t x t − 1 , β t I ) q(x_{t}|x_{t-1})=N(x_{t};\sqrt{1-\beta_{t}}x_{t-1},\beta_{t}I) q(xt∣xt−1)=N(xt;1−βtxt−1,βtI)
- t：time step时间步长
- x 0 x_{0} x0:真实数据分布中抽取的样本数据
- β t \beta_{t} βt:方差进度刻( 0 ≤ β t ≤ 1 0\leq\beta_{t}\leq1 0≤βt≤1, β 0 \beta_{0} β0小 → β T \rightarrow\beta_{T} →βT大)
- I I I:单位阵
- x t x_{t} xt:输出output，亦是经过t次添加噪声的数据
- 1 − β t x t − 1 \sqrt{1-\beta_{t}}x_{t-1} 1−βtxt−1:均值mean
- β t I \beta_{t}I βtI:方差variance
- 注：在正态分布中，各项参数依次是输出、均值、方差
逐步向图像中添加高斯噪声，从而迭代的产生样本 x 1 , . . . , x T x_{1},...,x_{T} x1,...,xT
当 T → ∞ T\rightarrow\infty T→∞，将有完全高斯噪声图像
采样方法：可使用一个封闭公式在特定时间步长对图像直接取样
封闭公式
可通过重新参数化技巧得到
若z时高斯分布 N ( μ , σ 2 ) N(\mu,\sigma^{2}) N(μ,σ2)的取样，则 z = μ + σ ϵ z=\mu+\sigma\epsilon z=μ+σϵ
- e p s i l o n epsilon epsilon是 N ( 0 , 1 ) N(0,1) N(0,1)的取样
又 μ = 1 − β t x t − 1 , σ 2 = β t I \mu=\sqrt{1-\beta_{t}}x_{t-1}, \sigma^{2}=\beta_{t}I μ=1−βtxt−1,σ2=βtI
令 α t = 1 − β t , α ‾ t = ∏ i − 1 t α i , ϵ i ∼ N ( 0 , I ) , ϵ ‾ i ∼ N ( 0 , 1 ) \alpha_{t}=1-\beta_{t},\overline{\alpha}_{t=\prod_{i-1}^t}\alpha_{i},\epsilon_{i}\sim N(0,I),\overline{\epsilon}_{i}\sim N(0,1) αt=1−βt,αt=∏i−1tαi,ϵi∼N(0,I),ϵi∼N(0,1)
x t = 1 − β t x t − 1 + β t ϵ t − 1 = α t ( α t − 1 x t − 2 + 1 − α t − 1 ϵ t − 2 ) + 1 − α t ϵ t − 1 = α t α t − 1 x t − 2 + ( 1 − α t − 1 ) α t ϵ t − 2 + 1 − α t ϵ t − 1 \begin{aligned}x_{t}&=\sqrt{1-\beta_{t}}x_{t-1}+\sqrt{\beta_{t}}\epsilon_{t-1}\\&=\sqrt{\alpha_{t}}(\sqrt{\alpha_{t-1}}x_{t-2}+\sqrt{1-\alpha_{t-1}}\epsilon_{t-2})+\sqrt{1-\alpha_{t}}\epsilon_{t-1}\\&=\sqrt{\alpha_{t}\alpha_{t-1}}x_{t-2}+\sqrt{(1-\alpha_{t-1})\alpha_{t}}\epsilon_{t-2}+\sqrt{1-\alpha_{t}}\epsilon_{t-1}\end{aligned} xt=1−βtxt−1+βtϵt−1=αt(αt−1xt−2+1−αt−1ϵt−2)+1−αtϵt−1=αtαt−1xt−2+(1−αt−1)αtϵt−2+1−αtϵt−1
X = ( 1 − α t − 1 ) α t ϵ t − 2 , Y = 1 − α t ϵ t − 1 X=\sqrt{(1-\alpha_{t-1})\alpha_{t}}\epsilon_{t-2}, Y=\sqrt{1-\alpha_{t}}\epsilon_{t-1} X=(1−αt−1)αtϵt−2,Y=1−αtϵt−1
∵ ϵ t − 2 , ϵ t − 1 ∼ N ( 0 , 1 ) \because \epsilon_{t-2}, \epsilon_{t-1} \sim N(0,1) ∵ϵt−2,ϵt−1∼N(0,1)
∴ α t ( 1 − α t − 1 ) ϵ t − 2 → X ∼ N ( 0 , α t ( 1 − α t − 1 ) I , 1 − α t − 1 ϵ t − 1 → Y ∼ N ( 0 , 1 − α t I ) \therefore \sqrt{\alpha_{t}(1-\alpha_{t-1})}\epsilon_{t-2}\rightarrow X \sim N(0,\alpha_{t}(1-\alpha_{t-1})I,\;\sqrt{1-\alpha_{t-1}}\epsilon_{t-1} \rightarrow Y \sim N(0,\sqrt{1-\alpha_{t}}I) ∴αt(1−αt−1)ϵt−2→X∼N(0,αt(1−αt−1)I,1−αt−1ϵt−1→Y∼N(0,1−αtI)
令 Z = X + Y Z=X+Y Z=X+Y，则有 Z ∼ N ( 0 , ( 1 − α t α t − 1 ) I ) Z \sim N(0,(1-\alpha_{t}\alpha_{t-1})I) Z∼N(0,(1−αtαt−1)I)
X + Y = 1 − α t α t − 1 ϵ ‾ t − 2 , ϵ ‾ t − 2 ∼ N ( 0 , 1 ) X+Y=\sqrt{1-\alpha_{t}\alpha_{t-1}}\overline{\epsilon}_{t-2},\;\overline{\epsilon}_{t-2} \sim N(0,1) X+Y=1−αtαt−1ϵt−2,ϵt−2∼N(0,1)
x t = α t α t − 1 x t − 2 + ( 1 − α t − 1 ) α t ϵ t − 2 + 1 − α t ϵ t − 1 = α t α t − 1 x t − 2 + X + Y = α t α t − 1 x t − 2 + 1 − α t α t − 1 ϵ ‾ t − 2 = α t α t − 1 … α 1 x 0 + 1 − α t α t − 1 … α 1 ϵ = α ‾ t x 0 + 1 − α ‾ t ϵ \begin{aligned}x_{t}&=\sqrt{\alpha_{t}\alpha_{t-1}}x_{t-2}+\sqrt{(1-\alpha_{t-1})\alpha_{t}}\epsilon_{t-2}+\sqrt{1-\alpha_{t}}\epsilon_{t-1}\\&=\sqrt{\alpha_{t}\alpha_{t-1}}x_{t-2}+X+Y\\&=\sqrt{\alpha_{t}\alpha_{t-1}}x_{t-2}+\sqrt{1-\alpha_{t}\alpha_{t-1}}\overline{\epsilon}_{t-2}\\&=\sqrt{\alpha_{t}\alpha_{t-1}\dots\alpha_{1}}x_{0}+\sqrt{1-\alpha_{t}\alpha_{t-1}\dots\alpha_{1}}\epsilon\\&=\sqrt{\overline{\alpha}_{t}x_{0}}+\sqrt{1-\overline{\alpha}_{t}}\epsilon\end{aligned} xt=αtαt−1xt−2+(1−αt−1)αtϵt−2+1−αtϵt−1=αtαt−1xt−2+X+Y=αtαt−1xt−2+1−αtαt−1ϵt−2=αtαt−1…α1x0+1−αtαt−1…α1ϵ=αtx0+1−αtϵ
令 ∏ i = 1 t α i = α ‾ t \prod^{t}_{i=1}\alpha_{i}=\overline{\alpha}_{t} ∏i=1tαi=αt，则有①式 x t = α ‾ t x 0 + 1 − α ‾ t ϵ x_{t}=\sqrt{\overline{\alpha}_{t}}x_{0}+\sqrt{1-\overline{\alpha}_{t}}\epsilon xt=αtx0+1−αtϵ
注：各 ϵ \epsilon ϵ是相互独立但取自相同分布的标准正态随机变量
①式可用于在任何时间步骤直接对 x t x_{t} xt采样
Reverse Diffusion Process反向扩散过程
该过程无法通过反转噪声实现，而需要训练神经网络approximated distribution p θ ( x t − 1 ∣ x t ) p_{\theta}(x_{t-1}|x_{t}) pθ(xt−1∣xt)来近似target distribution q ( x t − 1 ∣ x t ) q(x_{t-1}|x_{t}) q(xt−1∣xt)，其服从正态分布
目标分布target distribution： q ( x t − 1 ∣ x t ) = N ( x t − 1 ; μ ‾ ( x t , x 0 ) , β ‾ t I ) q(x_{t-1}|x_{t})=N(x_{t-1};\overline{\mu}(x_{t},x_{0}),\overline{\beta}_{t}I) q(xt−1∣xt)=N(xt−1;μ(xt,x0),βtI)
近似分布approximated distribution： p θ ( x t − 1 ∣ x t ) = N ( x t − 1 ; μ θ ( x t , t ) , ∑ θ ( x t , t ) ) p_{\theta}(x_{t-1}|x_{t})=N(x_{t-1};\mu_{\theta}(x_{t},t),\sum_{\theta}(x_{t},t)) pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),∑θ(xt,t))
{ μ ( x t , t ) : = μ ‾ t ( x t , x 0 ) ∑ θ ( x t , t ) : = β t I \begin{cases}\mu(x_{t},t):=\overline{\mu}_t(x_{t},x_{0})\\\sum_{\theta}(x_{t},t):=\beta_{t}I\end{cases} {μ(xt,t):=μt(xt,x0)∑θ(xt,t):=βtI
loss function损失函数
L O S S = − log ( p θ ( x 0 ) ) LOSS=-\log{(p_{\theta}(x_0))} LOSS=−log(pθ(x0))
其中 p θ ( x 0 ) p_{\theta}(x_{0}) pθ(x0)取决于 x 1 , x 2 , … , x T x_{1},x_{2},\dots,x_{T} x1,x2,…,xT，较为棘手，因此采用与VAE中的类似的方法，通过优化下阶，简介优化不可处理的损失函数，关于KL LOSS与VAE loss function详见VAE模型中的损失函数
Loss Function of VAE model VAE模型的损失函数
L O S S = M S E ( X , X ′ ) + K L ( N ( μ , σ 2 ) , N ( 0 , 1 ) ) LOSS=MSE(X,X')+KL(N(\mu,\sigma^{2}),N(0,1)) LOSS=MSE(X,X′)+KL(N(μ,σ2),N(0,1))
首项 M S E ( X , X ′ ) MSE(X,X') MSE(X,X′)称reconstruct loss 重构损失，反应生成结果与输入之间的差异
次项 K L ( N ( μ , σ 2 ) , N ( 0 , 1 ) ) KL(N(\mu,\sigma^{2}),N(0,1)) KL(N(μ,σ2),N(0,1))称KL lossKL散度正则项：在去除reconstruct loss的vae中其编码空间会呈现标准正态分布，故称其作用：使得编码器生成的隐藏变量尽可能符合标准正态分布
已知kl loss非负，故
− log p θ ( x 0 ) ≤ − log p θ ( x 0 ) + D K L ( q ( x 1 : T ∣ x 0 ) ∣ ∣ p θ ( x 1 : T ∣ x 0 ) ) -\log{p_{\theta}(x_{0})}\le-\log{p_{\theta}(x_0)}+D_{KL}(q(x_{1:T}|x_0)||p_\theta(x_{1:T}|x_0)) −logpθ(x0)≤−logpθ(x0)+DKL(q(x1:T∣x0)∣∣pθ(x1:T∣x0))
− log p θ ( x 0 ) ≤ E q [ log q ( x 1 : T ∣ x 0 ) p θ ( x 1 : T ) ] -\log{p_\theta(x_0)}\le E_q[\frac{\log{q(x_{1:T}|x_0)}}{p_\theta(x_{1:T})}] −logpθ(x0)≤Eq[pθ(x1:T)logq(x1:T∣x0)]tip:此处引入变分下界，详见变分推断
展开有 − log p θ ( x 0 ) ≤ E q [ D K L ( q ( x T ∣ x 0 ) ∣ ∣ p θ ( x T ) ) + ∑ t = 2 T D K L ( q ( x t − 1 ∣ x t , x 0 ) ∣ ∣ p θ ( x t − 1 ∣ x t ) ) ] − log p θ ( x 0 ∣ x 1 ) -\log{p_{\theta}(x_{0})}\le E_q[D_{KL}(q(x_T|x_0)||p_\theta(x_T))+\sum_{t=2}^TD_{KL}(q(x_{t-1}|x_t,x_0)||p_\theta(x_{t-1}|x_t))]-\log{p_\theta(x_0|x_1)} −logpθ(x0)≤Eq[DKL(q(xT∣x0)∣∣pθ(xT))+∑t=2TDKL(q(xt−1∣xt,x0)∣∣pθ(xt−1∣xt))]−logpθ(x0∣x1)
- 常数项 E q [ D K L ( q ( x T ∣ x 0 ) ∣ ∣ p θ ( x T ) ) E_q[D_{KL}(q(x_T|x_0)||p_\theta(x_T)) Eq[DKL(q(xT∣x0)∣∣pθ(xT))：q无可学习参数，q为高斯噪声概率，故本项为可忽略的常数项
- 逐步去噪项
∑
t
=
2
T
D
K
L
(
q
(
x
t
−
1
∣
x
t
,
x
0
)
∣
∣
p
θ
(
x
t
−
1
∣
x
t
)
)
]
\sum_{t=2}^TD_{KL}(q(x_{t-1}|x_t,x_0)||p_\theta(x_{t-1}|x_t))]
∑t=2TDKL(q(xt−1∣xt,x0)∣∣pθ(xt−1∣xt))]
- 真实分布
q
(
x
t
−
1
∣
x
t
,
x
0
)
=
N
(
x
t
−
1
;
μ
~
(
x
t
,
x
0
)
,
β
‾
t
I
)
q(x_{t-1}|x_t,x_0)=N(x_{t-1};\tilde\mu(x_t,x_0),\overline\beta_tI)
q(xt−1∣xt,x0)=N(xt−1;μ~(xt,x0),βtI)
-
μ
~
t
(
x
t
,
x
0
)
=
α
t
(
1
−
α
‾
t
−
1
)
1
−
α
‾
t
x
t
+
α
‾
t
−
1
β
t
1
−
α
‾
t
x
0
\tilde\mu_t(x_t,x_0)=\frac{\sqrt{\alpha_t}(1-\overline\alpha_{t-1})}{1-\overline\alpha_t}x_t+\frac{\sqrt{\overline\alpha_{t-1}}\beta_t}{1-\overline\alpha_t}x_0
μ~t(xt,x0)=1−αtαt(1−αt−1)xt+1−αtαt−1βtx0
- 又 x 0 = 1 α ‾ t ( x t − 1 − α ‾ ) t ϵ t ) x_0=\frac1{\sqrt{\overline\alpha_t}}(x_t-\sqrt{1-\overline\alpha)t}\epsilon_t) x0=αt1(xt−1−α)tϵt)
- 故 μ ~ t ( x t ) = 1 α t ( x t − 1 − α t 1 − α ‾ t ϵ t ) \tilde\mu_t(x_t)=\frac1{\sqrt{\alpha_t}}(x_t-\frac{1-\alpha_t}{\sqrt{1-\overline\alpha_t}}\epsilon_t) μ~t(xt)=αt1(xt−1−αt1−αtϵt)
- β ‾ t = 1 − α ‾ t − 1 1 − α ‾ t β ) t \overline\beta_t=\frac{1-\overline\alpha_{t-1}}{1-\overline\alpha_t}\beta)t βt=1−αt1−αt−1β)t
-
μ
~
t
(
x
t
,
x
0
)
=
α
t
(
1
−
α
‾
t
−
1
)
1
−
α
‾
t
x
t
+
α
‾
t
−
1
β
t
1
−
α
‾
t
x
0
\tilde\mu_t(x_t,x_0)=\frac{\sqrt{\alpha_t}(1-\overline\alpha_{t-1})}{1-\overline\alpha_t}x_t+\frac{\sqrt{\overline\alpha_{t-1}}\beta_t}{1-\overline\alpha_t}x_0
μ~t(xt,x0)=1−αtαt(1−αt−1)xt+1−αtαt−1βtx0
- 预测分布
p
θ
(
x
t
−
1
∣
x
t
)
)
=
N
(
x
t
−
1
;
μ
θ
(
x
t
,
t
)
,
β
t
I
)
p_\theta(x_{t-1}|x_t))=N(x_{t-1};\mu_\theta(x_t,t),\beta_tI)
pθ(xt−1∣xt))=N(xt−1;μθ(xt,t),βtI)
- μ θ ( x t , t ) \mu_\theta(x_t,t) μθ(xt,t)是由神经网络训练的部分
- 近似均值
μ
θ
\mu_\theta
μθ设置为与真实分布的均值
μ
‾
t
\overline\mu_t
μt（即目标均值）相同的形式
- target mean μ ‾ t ( x t ) = 1 α t ( x t − 1 − α t 1 − α ‾ t ϵ t ) \overline\mu_t(x_t)=\frac1{\sqrt{\alpha_t}}(x_t-\frac{1-\alpha_t}{\sqrt{1-\overline\alpha_t}}\epsilon_t) μt(xt)=αt1(xt−1−αt1−αtϵt)
- approximated mean μ θ ( x t , t ) = 1 α t ( x t − 1 − α t 1 − α ‾ t ϵ θ ( x t , t ) ) \mu_\theta(x_t,t)=\frac1{\sqrt{\alpha_t}}(x_t-\frac{1-\alpha_t}{\sqrt{1-\overline\alpha_t}}\epsilon_\theta(x_t,t)) μθ(xt,t)=αt1(xt−1−αt1−αtϵθ(xt,t))
- 二者的比较可以使用MSE进行
- 真实分布
q
(
x
t
−
1
∣
x
t
,
x
0
)
=
N
(
x
t
−
1
;
μ
~
(
x
t
,
x
0
)
,
β
‾
t
I
)
q(x_{t-1}|x_t,x_0)=N(x_{t-1};\tilde\mu(x_t,x_0),\overline\beta_tI)
q(xt−1∣xt,x0)=N(xt−1;μ~(xt,x0),βtI)
- 重构项
log
p
θ
(
x
0
∣
x
1
)
\log{p_\theta(x_0|x_1)}
logpθ(x0∣x1)
- 本项可以忽略，由于可用
L
t
−
1
L_{t-1}
Lt−1中相同神经网络进行拟合，且忽略使得样本质量更好实施
- 本项可以忽略，由于可用
L
t
−
1
L_{t-1}
Lt−1中相同神经网络进行拟合，且忽略使得样本质量更好实施
kl loss KL散度正则项
关于KL散度的解释
- 离散的kl loss
- D K L ( P ∣ ∣ Q ) = ∑ i = 1 N [ p ( x i ) log p ( x i ) − p ( x i ) log q ( x i ) ] D_{KL}(P||Q)=\sum_{i=1}^{N}[p(x_{i})\log{p(x_{i})}-p(x_{i})\log{q(x_{i})}] DKL(P∣∣Q)=∑i=1N[p(xi)logp(xi)−p(xi)logq(xi)]
- P为真实时间的概率分布，Q为理论拟合出的该事件的概率分布
- 两个概率分布之间的KL散度可以表达两个分布的相似性，例子如下
- 连续的kl loss
- D K L ( P ∣ ∣ Q ) = ∫ − ∞ + ∞ p ( x ) log ( p ( x ) q ( x ) ) d x D_{KL}(P||Q)=\int_{-\infty}^{+\infty}p(x)\log{(\frac{p(x)}{q(x)})}dx DKL(P∣∣Q)=∫−∞+∞p(x)log(q(x)p(x))dx
- 基本性质：非负、仿射变换不变性、非对易性、一定条件下
D
K
L
(
P
∣
∣
Q
)
D_{KL}(P||Q)
DKL(P∣∣Q)
- 仿射变换不变性
- ∵ y = a x + b ∴ D K L ( P ( x ) ∣ ∣ Q ( x ) ) = D K L ( P ( x ) ∣ ∣ Q ( y ) ) \because y=ax+b\therefore D_{KL}(P(x)||Q(x))=D_{KL}(P(x)||Q(y)) ∵y=ax+b∴DKL(P(x)∣∣Q(x))=DKL(P(x)∣∣Q(y))
- 多元正态分布的kl loss
- 设 P 1 ( x ) = N ( μ 1 , σ 1 2 ) , P 2 ( x ) = N ( μ 2 , σ 2 2 ) P_{1}(x)=N(\mu_{1},\sigma_{1}^{2}),P_{2}(x)=N(\mu_{2},\sigma^{2}_2) P1(x)=N(μ1,σ12),P2(x)=N(μ2,σ22)
- 则有 K L ( N ( μ , σ 1 2 ) , N ( μ 2 , σ 2 2 ) ) = − 1 2 + log ( σ 2 σ 1 ) + σ 1 2 + ( μ 1 − μ 2 ) 2 2 σ 2 2 KL(N(\mu,\sigma_{1}^{2}),N(\mu_{2},\sigma^{2}_2))=-\frac{1}{2}+\log{(\frac{\sigma_{2}}{\sigma_{1}})}+\frac{\sigma_{1}^{2}+(\mu_1-\mu_2)^2}{2\sigma_{2}^{2}} KL(N(μ,σ12),N(μ2,σ22))=−21+log(σ1σ2)+2σ22σ12+(μ1−μ2)2
- 若修改P2为 P 2 ( x ) = N ( 0 , 1 ) P_{2}(x)=N(0,1) P2(x)=N(0,1)，则有 K L ( N ( μ , σ 1 2 ) , N ( 0 , 1 ) ) = − 1 2 ( μ 1 2 + σ 1 2 − 2 log ( σ 1 ) − 1 ) KL(N(\mu,\sigma_{1}^{2}),N(0,1))=-\frac{1}{2}(\mu^{2}_{1}+\sigma_{1}^{2}-2\log{(\sigma_{1})}-1) KL(N(μ,σ12),N(0,1))=−21(μ12+σ12−2log(σ1)−1)
Variational Lower Bound变分下界
this part is mainly about variational inference.
变分推断可以针对贝叶斯统计中对于后验概率的计算，MCMC马尔科夫链蒙特卡洛方法对于大量数据计算较慢，而变分推断提供了更快更简单的近似推断方法
假定观测量 x ⃗ = x 1 : n \vec{x}=x_{1:n} x=x1:n，隐藏变量 z ⃗ = z 1 : m \vec{z}=z_{1:m} z=z1:m，推断问题需要推测后验条件概率分布 p ( z ⃗ ∣ x ⃗ ) p(\vec{z}|\vec{x}) p(z∣x)。变分法的基本思想是将该问题转化为优化问题。首先引入一族关于隐藏变量的近似概率分布Q，需要从中寻找一个与真实分布的KL Divergence的最小的分布，即 q ∗ ( z ⃗ ) = a r g m i n q ( z ⃗ ∈ Q ) K L ( q ( z ⃗ ) ∣ ∣ p ( z ⃗ ∣ x ⃗ ) ) q^{*}(\vec{z})=argmin_{q(\vec{z}\in Q)}KL(q(\vec{z})||p(\vec{z}|\vec{x})) q∗(z)=argminq(z∈Q)KL(q(z)∣∣p(z∣x))。可用 q ∗ ( z ⃗ ) q^{*}(\vec{z}) q∗(z)近似代替真实后验分布。将变分推断转换为求极值，可通过选择更合适的Q使得密度分布足够灵活，同时足够简单适于优化
注：
- 信息熵公式
H
(
x
)
=
−
∑
i
=
1
n
p
(
x
i
)
log
(
p
(
x
i
)
)
H(x)=-\sum^{n}_{i=1}p(x_{i})\log{(p(x_{i}))}
H(x)=−∑i=1np(xi)log(p(xi))
- 其中 p ( x i ) p(x_{i}) p(xi)代表随机事件的概率
- 对于同一个随机变量的两种不同分布P(x)和Q(x)可以使用KL Divergence来描述差异
- D K L ( P ∣ ∣ Q ) = E x P [ log P ( x ) Q ( x ) ] = E x P [ log P ( x ) − log Q ( x ) ] D_{KL}(P||Q)=E_{x~P}[\log{\frac{P(x)}{Q(x)}}]=E_{x~P}[\log{P(x)}-\log{Q(x)}] DKL(P∣∣Q)=Ex P[logQ(x)P(x)]=Ex P[logP(x)−logQ(x)]
变分推断详述
- from KL to ELBO
- K L ( q ( z ⃗ ) ∣ ∣ p ( z ⃗ ∣ x ⃗ ) ) = E [ log q ( z ⃗ ) ] − E [ log q ( z ⃗ ∣ x ⃗ ) ] = E [ log q ( z ⃗ ) ] − E [ log p ( z ⃗ , x ⃗ ) ] + log p ( x ⃗ ) \begin{aligned}KL(q(\vec{z})||p(\vec{z}|\vec{x})) &=E[\log{q(\vec{z})}]-E[\log{q(\vec{z}|\vec{x})}]\\&=E[\log{q(\vec{z})}]-E[\log{p(\vec{z},\vec{x})}]+\log{p(\vec{x})}\end{aligned} KL(q(z)∣∣p(z∣x))=E[logq(z)]−E[logq(z∣x)]=E[logq(z)]−E[logp(z,x)]+logp(x)
- 最后一项为 log p ( x ⃗ ) \log{p(\vec{x})} logp(x)，属于边缘分布问题难以求解。由于无法直接计算kl，所以改变优化目标维与KL前两项相关量ELBO(evidence lower bound)
- KaTeX parse error: Expected 'EOF', got '&' at position 8: ELBO(q)&̲=E[\log{p(\vec{…
- 上式为ELBO的公式，可以看作 log p ( z ⃗ ) − K L \log{p(\vec{z})}-KL logp(z)−KL
- ELBO各项直观解释
- E L B O ( q ) = E [ log ( z ⃗ ) ] + E [ log p ( x ⃗ ∣ z ⃗ ) ] − E [ log q ( z ⃗ ) ] = E [ log p ( x ⃗ ∣ z ⃗ ) ] − K L ( q ( z ⃗ ) ∣ ∣ p ( z ⃗ ) ) \begin{aligned}ELBO(q)&=E[\log{(\vec{z})}]+E[\log{p(\vec{x}|\vec{z})}]-E[\log{q(\vec{z})}]\\&=E[\log{p(\vec{x}|\vec{z})}]-KL(q(\vec{z})||p(\vec{z}))\end{aligned} ELBO(q)=E[log(z)]+E[logp(x∣z)]−E[logq(z)]=E[logp(x∣z)]−KL(q(z)∣∣p(z))
- 可将ELBO展开为首行的形式，根据首行可以转换为次行的形式
- 通过次行可以更直观的理解ELBO的作用。
- 首项为期望项，促使模型将隐藏变量集中于可解释的观察量配置上
- 次项为隐藏变量变分分布与先验分布的KL divergence的相反数，促使变分分布接近于先验分布
- ELBO名称来源
- ∵ E L B O ( q ) = log p ( x ⃗ ) − K L ( q ( z ⃗ ) ∣ ∣ p ( z ⃗ ∣ x ⃗ ) ) \because ELBO(q)=\log{p(\vec{x})}-KL(q(\vec{z})||p(\vec{z}|\vec{x})) ∵ELBO(q)=logp(x)−KL(q(z)∣∣p(z∣x))
- ∴ log p ( x ⃗ ) = K L ( q ( z ⃗ ) ∣ ∣ p ( z ⃗ ∣ x ⃗ ) ) + E L B O ( q ) \therefore \log{p(\vec{x})}=KL(q(\vec{z})||p(\vec{z}|\vec{x}))+ELBO(q) ∴logp(x)=KL(q(z)∣∣p(z∣x))+ELBO(q)
- ∵ K L ( q ( z ⃗ ) ∣ ∣ p ( z ⃗ ∣ x ⃗ ) ) ≥ 0 \because KL(q(\vec{z})||p(\vec{z}|\vec{x})) \geq 0 ∵KL(q(z)∣∣p(z∣x))≥0
- ∴ log p ( x ⃗ ) ≥ E L B O ( q ) \therefore \log{p(\vec{x})} \geq ELBO(q) ∴logp(x)≥ELBO(q)
- ELBO提供了 log p ( x ⃗ ) \log{p(\vec{x})} logp(x)的下限。当 q ( z ⃗ ) = p ( z ⃗ ∣ x ⃗ ) q(\vec{z})=p(\vec{z}|\vec{x}) q(z)=p(z∣x)时，有 log p ( x ⃗ ) = E L B O ( q ) \log{p(\vec{x})} = ELBO(q) logp(x)=ELBO(q)
近似概率分布的选择
- 可以选择平均场变分族，其假设隐藏变量间相互独立
- q ( z ⃗ ) = ∏ j = 1 m q j ( z j ) q(\vec{z})=\prod^{m}_{j=1}q_{j}(z_{j}) q(z)=∏j=1mqj(zj)
根据ELBO及平均场假设，可用coordinate ascent variational inference（坐标上升变分推断CAVI）
利用条件概率分布的链式法则有 p ( z 1 : m , x 1 : n ) = p ( x 1 : n ) ∏ j = 1 m p ( z j ∣ z 1 : ( j − 1 ) , x 1 : n ) p(z_{1:m},x_{1:n})=p(x_{1:n})\prod_{j=1}^{m}p(z_{j}|z_{1:(j-1)},x_{1:n}) p(z1:m,x1:n)=p(x1:n)∏j=1mp(zj∣z1:(j−1),x1:n)
变分分布的期望为 E [ log q ( z 1 : m ) ] = ∑ j = 1 m E j [ log q ( z j ) ] E[\log{q(z_{1:m})}] = \sum_{j=1}^{m}E_{j}[\log{q(z_{j})}] E[logq(z1:m)]=∑j=1mEj[logq(zj)]
此时，代入ELBO有
E L B O = E [ log ( z ⃗ ) ] + E [ log p ( x ⃗ ∣ z ⃗ ) ] − E [ log q ( z ⃗ ) ] = log p ( x 1 : n ) + ∑ j = 1 m E j [ log q ( z j ) ] − E j [ log q ( z j ) ] \begin{aligned}ELBO&=E[\log{(\vec{z})}]+E[\log{p(\vec{x}|\vec{z})}]-E[\log{q(\vec{z})}]\\&=\log{p(x_{1:n})}+\sum_{j=1}^{m}E_{j}[\log{q(z_{j})}]-E_{j}[\log{q(z_{j})}]\end{aligned} ELBO=E[log(z)]+E[logp(x∣z)]−E[logq(z)]=logp(x1:n)+j=1∑mEj[logq(zj)]−Ej[logq(zj)]
对 z k z_{k} zk求导并令其为零有 d E L B O d q ( z k ) = E − k [ log p ( z k ∣ z − k , x ) ] − log q ( z k ) − 1 = 0 \frac{dELBO}{dq(z_{k})}=E_{-k}[\log{p(z_{k}|z_{-k},x)}]-\log{q(z_{k})}-1=0 dq(zk)dELBO=E−k[logp(zk∣z−k,x)]−logq(zk)−1=0
由CAVI有更新形式 q ∗ ( z k ) q^{*}(z_{k}) q∗(zk) ∝ E [ log ( c o n d i t i o n a l ) ] E[\log{(conditional)}] E[log(conditional)]
UNet
每个训练轮次中各样本随机取步长t，各步长组合为嵌入向量，噪声依据步长生成
训练步骤
- 随机选取一个步长样本并编码
- 根据步长合成原图与高斯噪声为噪声图像
- 输入噪声图像和嵌入向量，经UNet处理后输出预测图像，将预测噪声与实际噪声比较
训练过程
- 重复以下直至契合
- x0为原始数据
- t为从1-T中抽取的一个数字
- ϵ \epsilon ϵ为正态分布N(0,1)
- 做梯度下降，对象为预测值与实际值方差
反向扩散过程
- xT为由N(0,1)生成噪声图像
- for t from T to 1:
- z由N(0,1)生成
- 若t>1，否则z置零
-
x
t
−
1
=
1
α
t
(
x
t
−
1
−
α
t
1
−
α
‾
t
ϵ
θ
(
x
t
,
t
)
)
+
σ
t
z
x_{t-1}=\frac1{\sqrt{\alpha_t}}(x_t-\frac{1-\alpha_t}{\sqrt{1-\overline\alpha_t}}\epsilon_\theta(x_t,t))+\sigma_tz
xt−1=αt1(xt−1−αt1−αtϵθ(xt,t))+σtz
- 处理前图像减去噪声图像生成去噪图像
- x t − 1 x_{t-1} xt−1去噪图像
- x t x_t xt处理前图像
- ϵ θ ( x t , t ) \epsilon_\theta(x_t,t) ϵθ(xt,t)噪声图像
- 返回x0
- x0:根据学习的均值 μ θ ( x , 1 ) \mu_\theta(x,1) μθ(x,1)生成的预测去噪图像
扩散模型的速度问题
扩散采样会迭代的项UNet提供完整尺寸图象获得结果，总扩散步数T和图像尺寸较大时较慢，由此引入稳定扩散stable diffusion
Stable Diffusion稳定扩散
潜在空间
训练自编码器E，学习将图像数据降维成潜在数据，然后用解码器D，将潜在数据解码成图像。降噪过程将对潜在空间进行
相当于由处理三维空间，转换为处理三维空间的照片
潜在空间的扩散
正向扩散、反向扩散过程的操作内容同扩散模型
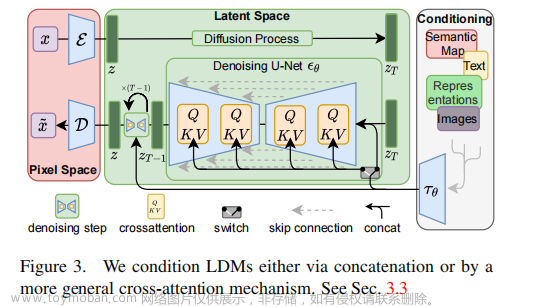
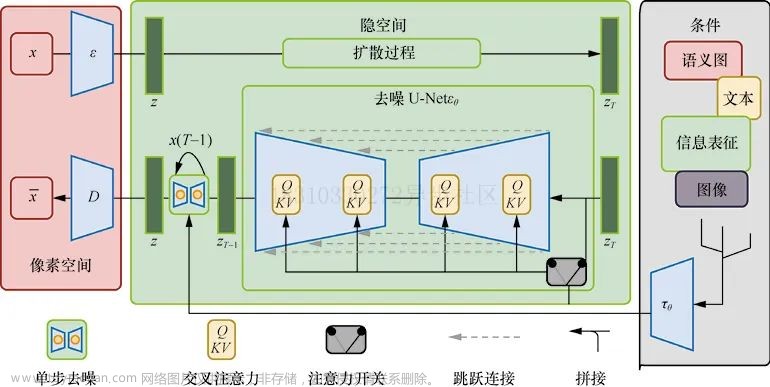
条件作用/调节
该模型在训练后可将文字编码后作为嵌入文本向量（额外输入），再输入随机潜在图像和步长嵌入向量，经扩散后解码成与文本有关的图像
通过使用交叉注意机制增强其去噪UNet，将内部扩散器转变为适应性(condition)图像生成器，通过开关调节输入，控制功能切换
- 非空间对齐输入（文本）：用语言模型转换为嵌入向量，然后映射至UNet
- 空间对齐输入：使用concat链接
训练
L L D M = E t , z 0 , ϵ , y [ ∣ ∣ ϵ − ϵ θ ( z t , t , τ θ ( y ) ) ∣ ∣ 2 ] L_{LDM}=E_{t,z_{0},\epsilon,y}[||\epsilon-\epsilon_\theta(z_t,t,\tau_\theta(y))||^2] LLDM=Et,z0,ϵ,y[∣∣ϵ−ϵθ(zt,t,τθ(y))∣∣2]
- τ θ ( y ) \tau_\theta(y) τθ(y)，适应性输入
-
z
t
=
(
α
‾
t
)
z
0
+
(
1
−
α
‾
t
)
ϵ
z_t=\sqrt(\overline\alpha_t)z_0+\sqrt(1-\overline\alpha_t)\epsilon
zt=(αt)z0+(1−αt)ϵ
- z 0 = E ( x 0 ) z_0=E(x_0) z0=E(x0)
架构比较
扩散模型框架
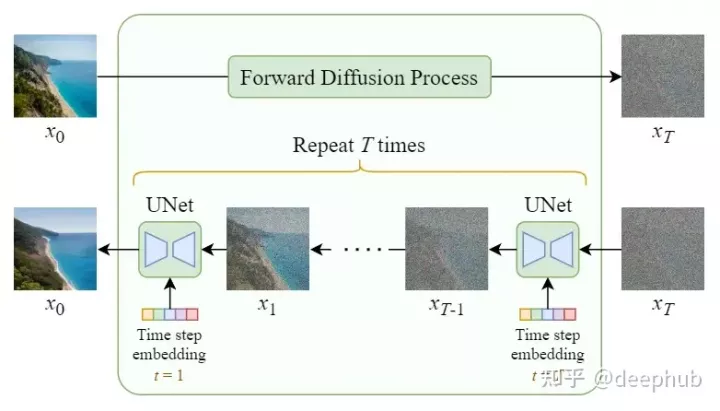
稳定扩散模型框架
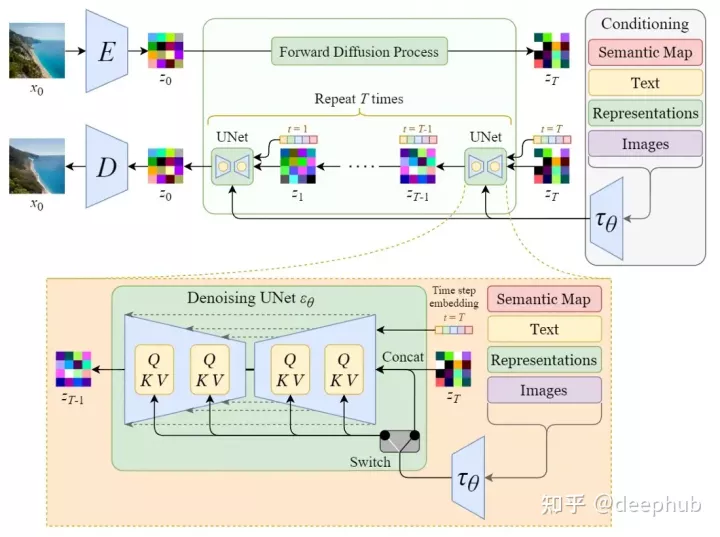文章来源：https://www.toymoban.com/news/detail-774283.html
与扩散模型相比，文章来源地址https://www.toymoban.com/news/detail-774283.html
- 输入为潜在数据，而采用潜在数据进行训练，训练速度更快
- 增加适应性输入，更富功能性
参考文章
- deephub,“Diffusion 和Stable Diffusion的数学和工作原理详细解释”,https://zhuanlan.zhihu.com/p/597924053
- 川陀学者,“变分推断——深度学习第十九章”,https://zhuanlan.zhihu.com/p/49401976
- David M. Blei, Alp Kucukelbir, Jon D. McAuliffe,“Variational Inference: A Review for Statisticians”，arXiv:1601.00670
- 捡到一束光,“关于KL散度（Kullback-Leibler Divergence）的笔记”,https://zhuanlan.zhihu.com/p/438129018
- 哇哦,“VAE模型解析（loss函数，调参…）”,https://zhuanlan.zhihu.com/p/578619659
到了这里，关于番外篇Diffusion&Stable Diffusion扩散模型与稳定扩散模型的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
