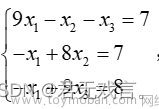1 背景简介
迭代法就是用某种极限过程去逐步逼近线性方程精确解的方法。迭代法具有需要计算机的存储单元较少、程序设计简单、原始系数矩阵在计算过程中始终不变等优点，但存在收敛性及收敛速度问题。
2 案例设计
3 数学模型
3.1 雅可比迭代法
3.1.1 算法过程
3.1.2 代码
function [xk,k] = Jacobi(A,b,x0)
D=diag(diag(A));
U=triu(A,1);
L=tril(A,-1);
BJ=-D\(L+U);
fJ=D\b;
xk=BJ*x0+fJ;
k=1;
while korm(xk-x0)>=1.0e-5
x0=xk;
xk=BJ*x0+fJ;
k=k+1;
end
end
%% 输入参数
% 输入系数矩阵
A = [5 2 1;-1 4 2;2 -3 10];
% 输入右端向量
b = [-12;20;3];
% 输入初始解
x0 = [1;1;1];
%% 用Jacobi迭代法解线性方程组
[xk,k] = Jacobi(A,b,x0)
3.1.3 计算结果
3.2 高斯-赛德尔迭代法
3.2.1 算法过程
3.2.2 代码
function [xk,k] = Seidel(A,b,x0)
D=diag(diag(A));
U=triu(A,1);
L=tril(A,-1);
BG=-(D+L)\U;
fG=(D+L)\b;
xk=BG*x0+fG;
k=1;
while norm(xk-x0)>=1.0e-5
x0=xk;
xk=BG*x0+fG;
k=k+1;
end
end
%% 输入参数
% 输入系数矩阵
A = [5 2 1;-1 4 2;2 -3 10];
% 输入右端向量
b = [-12;20;3];
% 输入初始解
x0 = [1;1;1];
%% 用Seidel迭代法解线性方程组
[xk,k] = Seidel(A,b,x0)
3.2.3 计算结果
3.3 超松弛迭代法
3.3.1 算法过程
3.3.2 代码
function [xk,k] = Sor(A,b,w,x0)
D=diag(diag(A));
U=-triu(A,1);
L=-tril(A,-1);
lw=(D-w*L)\((1-w)*D+w*U);
f=(D-w*L)\b*w;
xk=lw*x0+f;
k=1;
while norm(xk-x0)>=1.0e-5
x0=xk;
xk=lw*x0+f;
k=k+1;
end
end
%% 输入参数
% 输入系数矩阵
A = [5 2 1;-1 4 2;2 -3 10];
% 输入右端向量
b = [-12;20;3];
% 输入初始解
x0 = [0;0;0];
% 输入松弛参数
w = 0.7;
%% 用SOR迭代法解线性方程组
[xk,k] = Sor(A,b,w,x0)
3.3.3 计算结果
文章来源：https://www.toymoban.com/news/detail-774285.html
4 分析与讨论
雅可比迭代法、高斯-赛德尔迭代法、超松弛迭代法具有存储空间小、程序简单等特点，是解大型稀疏线性方程组的有效方法。从计算结果看，高斯-赛德尔迭代法比雅可比迭代法收敛得快，这与高斯-赛德尔迭代法不断利用最新算出来的近似解的分量有关。而松弛参数的选取对于超松弛迭代法的计算量影响很大，要选出最优松弛参数也是比较困难的。在最优松弛参数的情况下，超松弛迭代法的收敛速度将快于雅可比迭代法和高斯-赛德尔迭代法。文章来源地址https://www.toymoban.com/news/detail-774285.html
到了这里，关于【数值分析实验】（五）线性方程组的迭代解法（含matlab代码）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
