目录
一、引言
二、图的基本概念
三、图的存储方式
1. 邻接矩阵
2. 邻接表
3. 十字链表
4. 邻接多重表
四、邻接表的实现
1. 邻接表的定义
2. 邻接表的构建
3. 邻接表的遍历
五、邻接表的优缺点
六、总结
一、引言
在计算机科学中,图是一种非常重要的数据结构,它是由节点和边组成的一种数据结构,可以用来表示各种实际问题,如社交网络、路线规划等。在图的存储方式中,邻接表是一种常用的方式,它可以有效地表示图的结构,并且具有较高的效率。本文将介绍图的基本概念、存储方式以及邻接表的实现方法,希望能够帮助读者更好地理解和应用图的相关知识。
二、图的基本概念
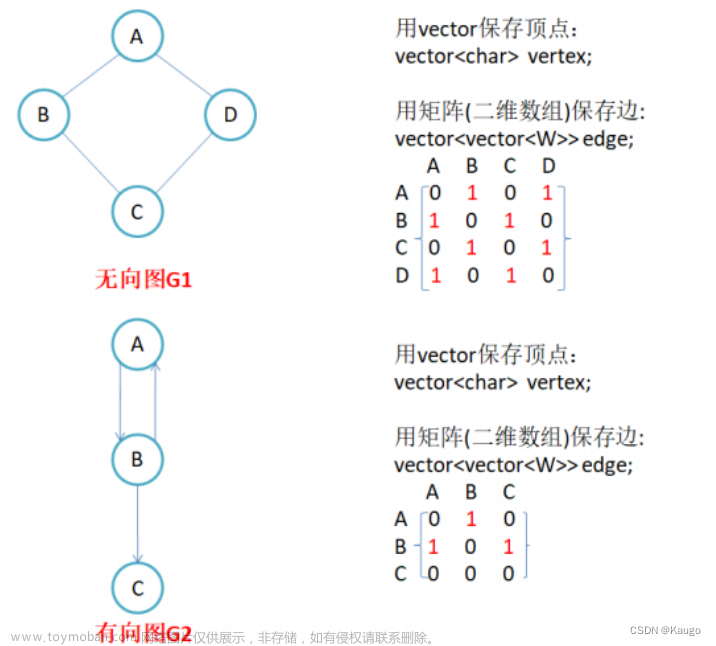
在图的定义中,有两个基本概念:节点和边。节点也称为顶点,是图中的基本元素,通常用一个圆圈或方框表示。边是节点之间的连接关系,通常用一条线段表示。图可以分为有向图和无向图两种类型,有向图中的边是有方向的,而无向图中的边是无方向的。
图的表示方法有多种,其中最常用的是邻接矩阵和邻接表。邻接矩阵是一个二维数组,其中每个元素表示两个节点之间是否有边相连。如果节点i和节点j之间有边相连,则邻接矩阵中第i行第j列的元素为1,否则为0。邻接矩阵的缺点是空间复杂度较高,当图的节点数较大时,会占用大量的内存空间。
三、图的存储方式
1. 邻接矩阵
邻接矩阵是一种常用的图的存储方式,它可以用一个二维数组表示图的结构。在邻接矩阵中,每个元素表示两个节点之间是否有边相连。如果节点i和节点j之间有边相连,则邻接矩阵中第i行第j列的元素为1,否则为0。
邻接矩阵的优点是可以快速地判断两个节点之间是否有边相连,时间复杂度为O(1)。但是邻接矩阵的缺点是空间复杂度较高,当图的节点数较大时,会占用大量的内存空间。
以下是C++实现邻接矩阵的构造、析构、深度优先遍历、广度优先遍历的代码:
#include <iostream>
#include <queue>
using namespace std;
const int MAXN = 100; // 最大顶点数
const int INF = 0x3f3f3f3f; // 无穷大
class Graph {
private:
int n; // 顶点数
int e; // 边数
int **matrix; // 邻接矩阵
public:
Graph(int n, int e); // 构造函数
~Graph(); // 析构函数
void addEdge(int u, int v, int w); // 添加边
void dfs(int u, bool visited[]); // 深度优先遍历
void bfs(int u); // 广度优先遍历
};
Graph::Graph(int n, int e) {
this->n = n;
this->e = e;
matrix = new int*[n];
for (int i = 0; i < n; i++) {
matrix[i] = new int[n];
for (int j = 0; j < n; j++) {
matrix[i][j] = INF; // 初始化为无穷大
}
}
}
Graph::~Graph() {
for (int i = 0; i < n; i++) {
delete[] matrix[i];
}
delete[] matrix;
}
void Graph::addEdge(int u, int v, int w) {
matrix[u][v] = w;
matrix[v][u] = w; // 无向图需要反向也加一次
}
void Graph::dfs(int u, bool visited[]) {
visited[u] = true;
cout << u << " ";
for (int v = 0; v < n; v++) {
if (matrix[u][v] != INF && !visited[v]) {
dfs(v, visited);
}
}
}
void Graph::bfs(int u) {
bool visited[MAXN] = {false};
queue<int> q;
visited[u] = true;
q.push(u);
while (!q.empty()) {
int v = q.front();
q.pop();
cout << v << " ";
for (int w = 0; w < n; w++) {
if (matrix[v][w] != INF && !visited[w]) {
visited[w] = true;
q.push(w);
}
}
}
}
int main() {
int n = 5, e = 6;
Graph g(n, e);
g.addEdge(0, 1, 1);
g.addEdge(0, 2, 1);
g.addEdge(1, 3, 1);
g.addEdge(2, 3, 1);
g.addEdge(2, 4, 1);
g.addEdge(3, 4, 1);
bool visited[MAXN] = {false};
cout << "DFS: ";
g.dfs(0, visited);
cout << endl;
cout << "BFS: ";
g.bfs(0);
cout << endl;
return 0;
}其中,构造函数和析构函数分别用于创建和销毁邻接矩阵。addEdge函数用于添加边,其中u和v表示边的两个顶点,w表示边的权值。dfs函数用于深度优先遍历,其中u表示当前遍历的顶点,visited数组表示顶点是否被访问过。bfs函数用于广度优先遍历,其中u表示起始顶点。在主函数中,我们创建了一个5个顶点6条边的图,并分别进行了深度优先遍历和广度优先遍历。
2. 邻接表
邻接表是一种常用的图的存储方式,它可以用链表表示图的结构。在邻接表中,每个节点都对应一个链表,链表中存储了与该节点相连的所有节点。邻接表的优点是空间复杂度较低,当图的节点数较大时,占用的内存空间较小。
3. 十字链表
十字链表是一种常用的有向图的存储方式,它可以用链表表示图的结构。在十字链表中,每个节点都对应一个链表,链表中存储了该节点的入边和出边。十字链表的优点是可以快速地遍历图中的所有节点和边。
以下是C++实现的图十字链表,附带注释解释每个函数的作用:
#include <iostream>
#include <vector>
using namespace std;
// 十字链表节点
struct OLNode {
int row, col; // 行列坐标
int weight; // 权重
OLNode* right; // 右指针
OLNode* down; // 下指针
};
// 十字链表头结点
struct HeadNode {
int row, col; // 行列坐标
OLNode* right; // 右指针
HeadNode* down; // 下指针
};
// 图十字链表
class GraphOL {
public:
GraphOL(int n) {
// 初始化头结点数组
headNodes.resize(n);
for (int i = 0; i < n; i++) {
headNodes[i].row = i;
headNodes[i].right = nullptr;
headNodes[i].down = nullptr;
}
}
// 添加边
void addEdge(int from, int to, int weight) {
// 创建新节点
OLNode* node = new OLNode();
node->row = to;
node->col = from;
node->weight = weight;
node->right = nullptr;
node->down = nullptr;
// 找到from对应的头结点
HeadNode* head = &headNodes[from];
// 如果头结点的右指针为空,直接将新节点挂在右指针上
if (head->right == nullptr) {
head->right = node;
}
else {
// 否则,找到最后一个节点,将新节点挂在其右侧
OLNode* p = head->right;
while (p->right != nullptr) {
p = p->right;
}
p->right = node;
}
// 找到to对应的头结点
head = &headNodes[to];
// 如果头结点的下指针为空,直接将新节点挂在下指针上
if (head->down == nullptr) {
head->down = node;
}
else {
// 否则,找到最后一个节点,将新节点挂在其下侧
OLNode* p = head->down;
while (p->down != nullptr) {
p = p->down;
}
p->down = node;
}
}
// 打印图
void print() {
for (int i = 0; i < headNodes.size(); i++) {
HeadNode* head = &headNodes[i];
OLNode* p = head->right;
while (p != nullptr) {
cout << "(" << p->col << ", " << p->row << ", " << p->weight << ") ";
p = p->right;
}
cout << endl;
}
}
private:
vector<HeadNode> headNodes; // 头结点数组
};4. 邻接多重表
邻接多重表是一种基于邻接表的存储方式,它将每条边表示为一个结构体,结构体中包含了两个指针,分别指向这条边的两个顶点。这种存储方式可以有效地避免重复边的出现,同时也可以方便地实现图的遍历。
四、邻接表的实现
1. 邻接表的定义
邻接表是一种基于链表的存储方式,它将每个顶点的所有邻接点存储在一个链表中。具体来说,邻接表由一个顶点数组和一个边链表组成,顶点数组中的每个元素表示一个顶点,边链表中的每个结点表示一条边。
以下是C++中图的邻接表的定义:
#include <iostream>
#include <vector>
using namespace std;
// 邻接表中的边结构体
struct Edge {
int to; // 目标节点
int weight; // 权重
Edge(int t, int w) : to(t), weight(w) {}
};
// 邻接表中的节点结构体
struct Node {
int val; // 节点的值
vector<Edge> neighbors; // 邻居节点
Node(int v) : val(v) {}
};
// 图的邻接表结构体
struct Graph {
vector<Node> nodes; // 节点集合
Graph(int n) {
for (int i = 0; i < n; i++) {
nodes.push_back(Node(i));
}
}
};
int main() {
Graph g(5);
g.nodes[0].neighbors.push_back(Edge(1, 2));
g.nodes[0].neighbors.push_back(Edge(2, 3));
g.nodes[1].neighbors.push_back(Edge(2, 4));
g.nodes[2].neighbors.push_back(Edge(3, 5));
g.nodes[3].neighbors.push_back(Edge(4, 6));
return 0;
}邻接表是一种表示图的数据结构,它通过将每个节点的邻居节点列表存储在该节点的数据结构中来表示图。在邻接表中,每个节点都是一个包含邻居节点列表的结构体,邻居节点列表中存储了该节点与其它节点之间的边。邻接表的优点是可以快速访问每个节点的邻居节点,因此它在处理稀疏图时比邻接矩阵更有效。在邻接表中,每个节点的邻居节点列表通常是一个动态数组或链表。
2. 邻接表的构建
邻接表的构建需要遍历图中的所有顶点和边,将它们按照一定的规则存储在顶点数组和边链表中。具体来说,可以使用一个数组来存储顶点,数组中的每个元素包含了该顶点的信息和一个指针,指向该顶点的邻接点链表。邻接点链表中的每个结点包含了该邻接点的信息和一个指针,指向下一个邻接点。
邻接表是一种常用的图的存储方式,它通过链表的方式存储每个节点的邻居节点,可以有效地节省空间。下面是一个简单的C++实现:
#include <iostream>
#include <vector>
using namespace std;
// 邻接表节点
struct AdjListNode {
int dest; // 目标节点
AdjListNode* next; // 指向下一个邻居节点的指针
};
// 图类
class Graph {
private:
int V; // 图的顶点数
vector<AdjListNode*> adjList; // 邻接表
public:
Graph(int V) {
this->V = V;
adjList.resize(V, nullptr); // 初始化邻接表
}
// 添加边
void addEdge(int src, int dest) {
// 创建新的邻接表节点
AdjListNode* newNode = new AdjListNode;
newNode->dest = dest;
newNode->next = nullptr;
// 将新节点插入到源节点的邻接表中
if (adjList[src] == nullptr) {
adjList[src] = newNode;
} else {
AdjListNode* cur = adjList[src];
while (cur->next != nullptr) {
cur = cur->next;
}
cur->next = newNode;
}
// 由于是无向图,所以还需要将目标节点的邻接表中插入源节点
newNode = new AdjListNode;
newNode->dest = src;
newNode->next = nullptr;
if (adjList[dest] == nullptr) {
adjList[dest] = newNode;
} else {
AdjListNode* cur = adjList[dest];
while (cur->next != nullptr) {
cur = cur->next;
}
cur->next = newNode;
}
}
// 打印邻接表
void printAdjList() {
for (int i = 0; i < V; i++) {
cout << i << ": ";
AdjListNode* cur = adjList[i];
while (cur != nullptr) {
cout << cur->dest << " ";
cur = cur->next;
}
cout << endl;
}
}
};
int main() {
Graph g(5);
g.addEdge(0, 1);
g.addEdge(0, 4);
g.addEdge(1, 2);
g.addEdge(1, 3);
g.addEdge(1, 4);
g.addEdge(2, 3);
g.addEdge(3, 4);
g.printAdjList();
return 0;
}在这个实现中,我们使用了一个结构体`AdjListNode`来表示邻接表中的每个节点,其中`dest`表示目标节点的编号,`next`表示指向下一个邻居节点的指针。我们还定义了一个`Graph`类来表示整个图,其中`V`表示图的顶点数,`adjList`是一个`vector`,用来存储每个节点的邻接表。
在`addEdge`函数中,我们首先创建一个新的邻接表节点,并将其插入到源节点的邻接表中。如果源节点的邻接表为空,则直接将新节点作为邻接表的头节点;否则,我们需要遍历邻接表,找到最后一个节点,然后将新节点插入到其后面。由于是无向图,所以我们还需要将目标节点的邻接表中插入源节点。
最后,我们定义了一个`printAdjList`函数来打印整个邻接表。对于每个节点,我们遍历其邻接表中的所有节点,并打印出目标节点的编号。
以上就是一个简单的图的邻接表的构建的C++实现。
3. 邻接表的遍历
邻接表的遍历可以通过遍历顶点数组和边链表来实现。具体来说,可以使用深度优先搜索或广度优先搜索算法来遍历邻接表中的所有顶点和边。
以下是C++代码,实现了图的深度优先遍历和广度优先遍历,注释中有详细的解释:
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
// 定义图的邻接表结构体
struct Graph {
int V; // 顶点数
vector<vector<int>> adj; // 邻接表
};
// 初始化图
Graph initGraph(int V) {
Graph G;
G.V = V;
G.adj.resize(V);
return G;
}
// 添加边
void addEdge(Graph& G, int u, int v) {
G.adj[u].push_back(v);
G.adj[v].push_back(u);
}
// 深度优先遍历
void DFS(Graph& G, int v, vector<bool>& visited) {
visited[v] = true;
cout << v << " ";
for (int u : G.adj[v]) {
if (!visited[u]) {
DFS(G, u, visited);
}
}
}
// 广度优先遍历
void BFS(Graph& G, int v, vector<bool>& visited) {
queue<int> q;
visited[v] = true;
q.push(v);
while (!q.empty()) {
int u = q.front();
q.pop();
cout << u << " ";
for (int w : G.adj[u]) {
if (!visited[w]) {
visited[w] = true;
q.push(w);
}
}
}
}
int main() {
int V = 5;
Graph G = initGraph(V);
addEdge(G, 0, 1);
addEdge(G, 0, 2);
addEdge(G, 1, 2);
addEdge(G, 2, 3);
addEdge(G, 3, 4);
vector<bool> visited(V, false);
cout << "DFS: ";
DFS(G, 0, visited);
cout << endl;
visited.assign(V, false);
cout << "BFS: ";
BFS(G, 0, visited);
cout << endl;
return 0;
}
在主函数中,我们首先初始化了一个5个顶点的图,并添加了5条边。然后分别进行了深度优先遍历和广度优先遍历,并输出了遍历结果。
深度优先遍历的实现使用了递归,从起点开始,依次遍历与其相邻的未访问过的顶点,直到所有顶点都被访问过为止。
广度优先遍历的实现使用了队列,从起点开始,依次将其相邻的未访问过的顶点加入队列中,并依次访问队列中的顶点,直到所有顶点都被访问过为止。
五、邻接表的优缺点
邻接表的优点在于它可以有效地存储稀疏图,同时也可以方便地实现图的遍历。缺点在于它无法快速地判断两个顶点之间是否存在边,需要遍历链表才能确定。文章来源:https://www.toymoban.com/news/detail-774468.html
六、总结
邻接表是一种基于链表的图存储方式,它可以有效地存储稀疏图,并且可以方便地实现图的遍历。但是它无法快速地判断两个顶点之间是否存在边,需要遍历链表才能确定。文章来源地址https://www.toymoban.com/news/detail-774468.html
到了这里,关于数据结构-图的邻接表的定义与实现的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!