头歌二叉树的二叉链表存储及基本操作-Toy模板网

这篇具有很好参考价值的文章主要介绍了头歌二叉树的二叉链表存储及基本操作。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

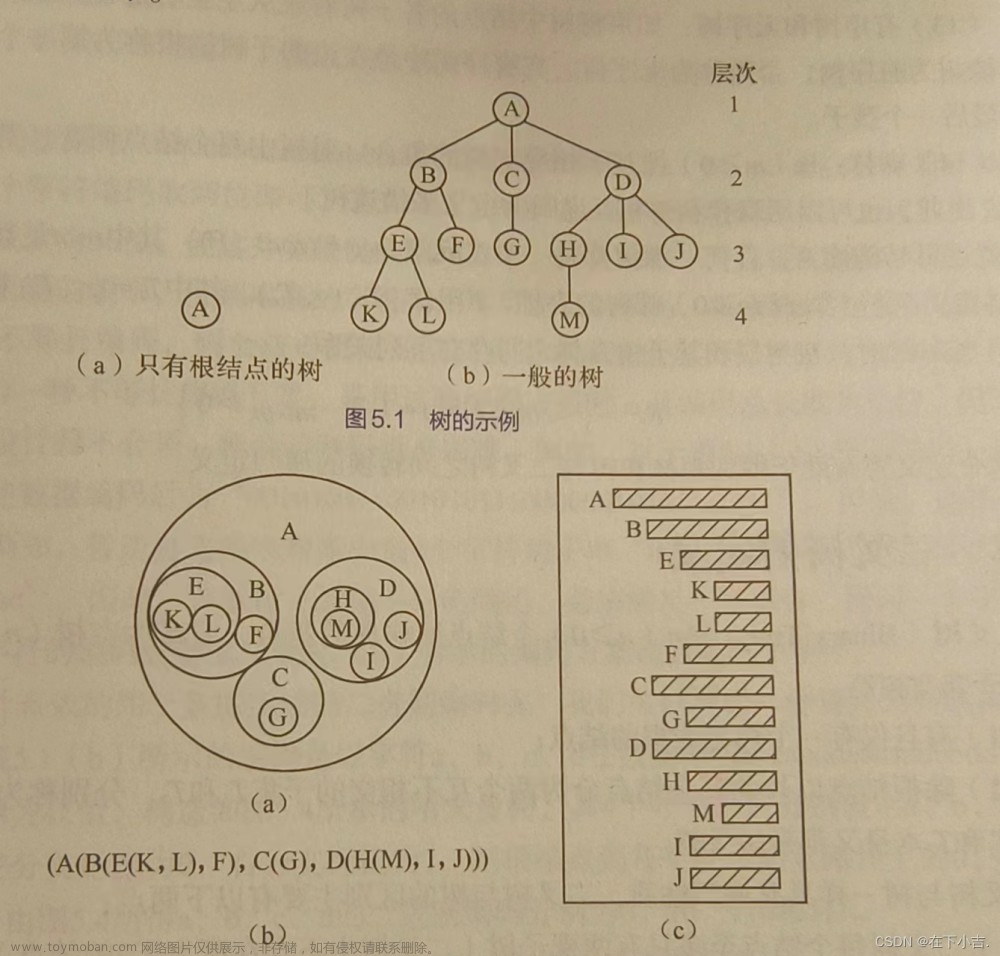
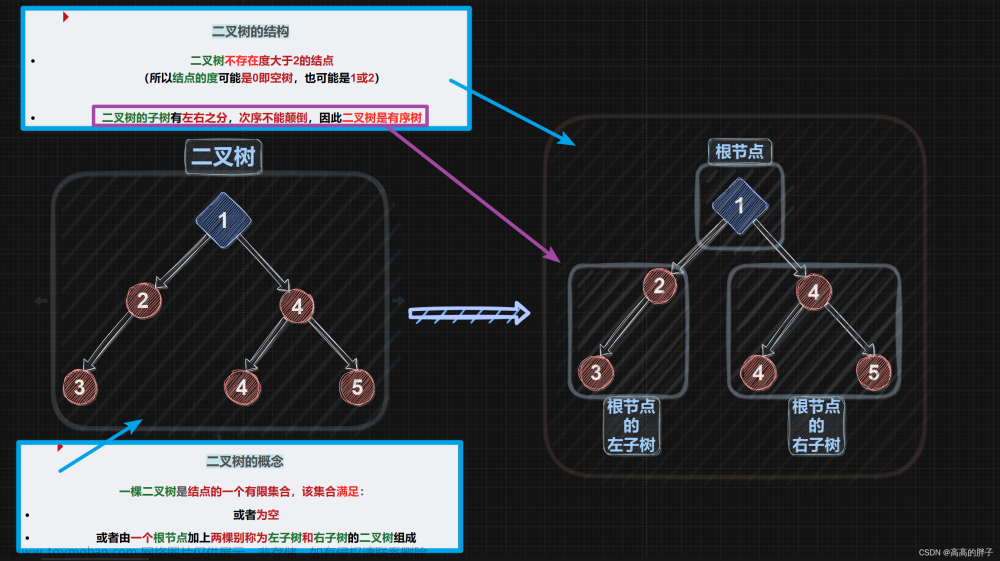
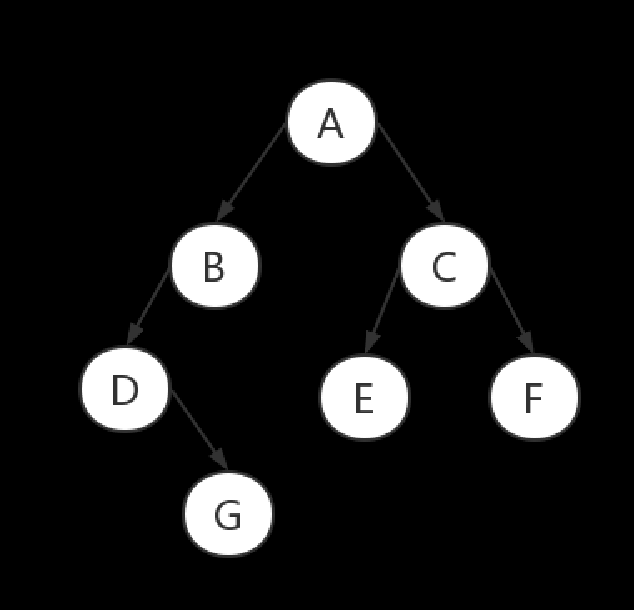
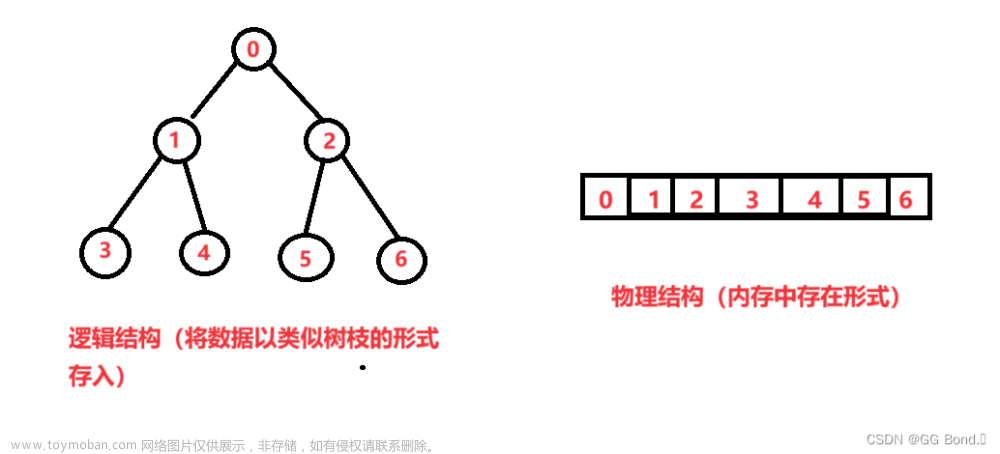
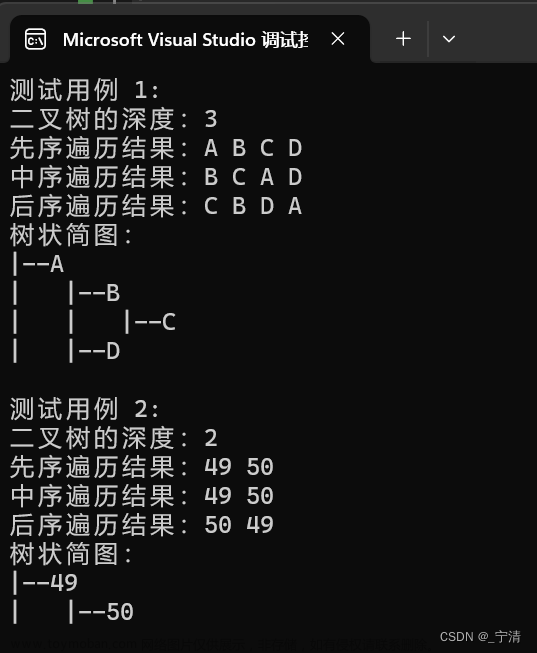
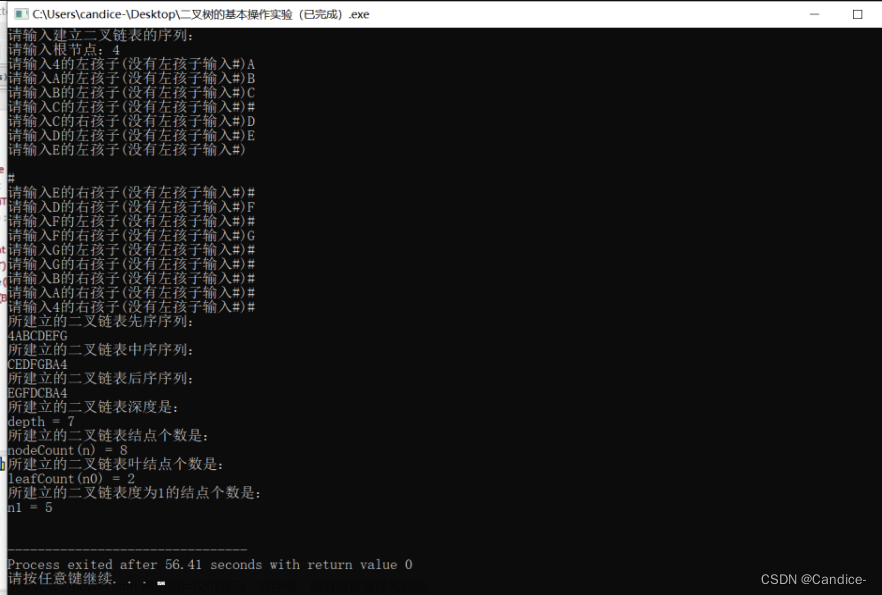
第1关先序遍历创建二叉链表存储的二叉树及遍历操作

void CreateBiTree(BiTree &T)
{  //按先序次序输入二叉树中结点的值
   // 构造二叉链表表示的二叉树T。变量Nil表示空(子)树。
  /********** Begin **********/ 
  
   // if (!T) return ;
   TElemType data;
   input(data);
   if(data == Nil) {
      return ;
   }
   T = (BiTree)malloc(sizeof(BiTNode));
   if(!T) return;
   T->data = data;
   CreateBiTree(T->lchild);
   CreateBiTree(T->rchild);
    
  /********** End **********/
}
 int  BiTreeEmpty(BiTree T)
 { // 初始条件：二叉树T存在。操作结果：若T为空二叉树，则返回TRUE，否则FALSE
    /********** Begin **********/ 
   if(!T){
      // if(T->data == Nil) return TRUE;
      // else return FALSE;
      return TRUE;
   }
   else return FALSE;
   /********** End **********/
}
void ProOrderTraverse(BiTree T,void(*Visit)(TElemType))
{ // 采用二叉链表存储结构，Visit是对数据元素操作的应用函数。
   // 先序遍历二叉树T的递归算法，对每个数据元素调用函数Visit
    /********** Begin **********/ 
   if (!T) {
      return ;
    }
    Visit(T->data);
    ProOrderTraverse(T->lchild,Visit);
    ProOrderTraverse(T->rchild,Visit);
    /********** End **********/
 }
void InOrderTraverse(BiTree T,void(*Visit)(TElemType))
{ // 采用二叉链表存储结构，Visit是对数据元素操作的应用函数。
   // 中序遍历二叉树T的递归算法，对每个数据元素调用函数Visit
    /********** Begin **********/ 
    if(!T){
      return;
    }
   InOrderTraverse(T->lchild,Visit);
   Visit(T->data);
   InOrderTraverse(T->rchild,Visit);
    
   /********** End **********/
 }
void PostOrderTraverse(BiTree T,void(*Visit)(TElemType))
{ // 初始条件：二叉树T存在，Visit是对结点操作的应用函数
   // 操作结果：后序递归遍历T，对每个结点调用函数Visit一次且仅一次
    /********** Begin **********/ 
    if(!T){
       return ; 
    }
    PostOrderTraverse(T->lchild,Visit);
    PostOrderTraverse(T->rchild,Visit);
    Visit(T->data);
     /********** End **********/
}
void DestoryBiTree(BiTree &T)
{  // 初始条件：二叉树T存在。操作结果：销毁二叉树T
    /********** Begin  **********/
   if(!T){
      return ;
   }
   DestoryBiTree(T->lchild);
   DestoryBiTree(T->rchild);
   free(T);
    /********** End **********/
}

第2关计算二叉树的高度、总节点个数和叶子节点个数

int BiTreeDepth(BiTree T)
{	 // 初始条件：二叉树T存在。操作结果：返回T的深度
    /********** Begin **********/ 
	if(!T) return 0;
    int lchild = BiTreeDepth(T->lchild);
    int rchild = BiTreeDepth(T->rchild);
    return 1+( 1+lchild>1+rchild?lchild:rchild);
    // return 1+lchild+rchild;
     /********** End **********/
}


int NodeCount(BiTree T)
{
	//初始条件：二叉树T存在。操作结果：返回T的结点数
    /********** Begin **********/
	if(!T) return 0;
    int lchild = NodeCount(T->lchild);
    int rchild = NodeCount(T->rchild);
    return 1+lchild+rchild;
    // return 1 + lchild + rchild;
    /********** End **********/
}


int LeafNodeCount(BiTree T)
{
	//初始条件：二叉树T存在。操作结果：返回T的叶子结点数
    /********** Begin **********/
	if(!T) return 0;
    if(!T->lchild && !T->rchild) return 1;
    return LeafNodeCount(T->lchild) + LeafNodeCount(T->rchild);
	/********** End **********/
}

第3关层次遍历二叉树

void LevelOrderTraverse(BiTree T,void(*Visit)(TElemType))
 { // 初始条件：二叉树T存在，Visit是对结点操作的应用函数
   // 操作结果：层序递归遍历T(利用队列)，对每个结点调用函数Visit一次且仅一次
    /********** Begin **********/ 
    if(!T) return ;
    BiTree p;
    LinkQueue q;
    InitQueue(q);  // 创建队列
    // 入队操作
    EnQueue(q,T);
    while(!QueueEmpty(q)){
      DeQueue(q,p);

      Visit(p->data);
      if(p->lchild){
        EnQueue(q,p->lchild);
      }
      if(p->rchild){
        EnQueue(q,p->rchild);
      }
    }
    DestroyQueue(q);
    /********** End **********/
}

第4关递归实现二叉树左右子树交换

void exchange ( BiTree T )
{
  // 实现二叉树左右子树的交换（递归法）
  /********** Begin *********/
  
  if(!T) return ;
  BiTree temp;

  exchange(T->lchild);
  exchange(T->rchild);
  
  temp = T->rchild;
  T->rchild = T->lchild;
  T->lchild = temp;
  
	/********** End **********/
}

第5关非递归实现二叉树左右子树交换

void exchange(BiTree T)
{
  // 实现二叉树左右子树的交换（栈实现）
  /********** Begin *********/
  SqStack s;
  BiTree p,temp;
  InitStack(s);
  if(!T) return;
  Push(s,T);
  while(!StackEmpty(s)){
    Pop(s,p);
    if(p->rchild){
      Push(s,p->rchild);
    }
    if(p->lchild){
      Push(s,p->lchild);
    }
    temp = p->lchild;
    p->lchild = p->rchild;
    p->rchild = temp;
  }
  /********** End **********/
}

第6关非递归实现二叉树的中序遍历文章来源地址https://www.toymoban.com/news/detail-774786.html

void InOrderTraverse2(BiTree T,void(*Visit)(TElemType))
{  // 采用二叉链表存储结构，Visit是对数据元素操作的应用函数。
   // 中序遍历二叉树T的非递归算法，对每个数据元素调用函数Visit
  /********** Begin *********/
  
  if(!T) return ;
  
  SqStack s;
  InitStack(s);
  BiTree p = T;
  while(!StackEmpty(s)||p){
      while(p){
          Push(s,p);
          p = p->lchild;
      }
      Pop(s,p);
      Visit(p->data);
        p = p->rchild;
    }
    DestroyStack(s);

  /********** End **********/
 }

到了这里，关于头歌二叉树的二叉链表存储及基本操作的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！