如果这篇文章对你有帮助,欢迎点赞与收藏~
基本概念
假设检验是一种统计决策过程,用于判断样本数据是否支持某个特定的假设。主要有两类假设:
零假设(Null Hypothesis):通常表示为没有效应或差异的假设。
备择假设(Alternative Hypothesis):表示有效应或差异的假设。
假设检验的步骤
定义假设:首先明确零假设和备择假设。
选择合适的检验:根据数据类型和研究目的选择适当的统计检验,如t检验、卡方检验等。
确定显著性水平:通常选择α=0.05,意味着5%的错误接受率。
计算检验统计量:使用样本数据计算出统计量。
作出决策:根据统计量和显著性水平判断是否拒绝零假设。
错误类型
第一类错误:错误地拒绝了真实的零假设(假阳性)。
第二类错误:没有拒绝一个错误的零假设(假阴性)。
在数学建模中的应用
假设检验在数学建模中有广泛的应用,例如:
模型验证:检验模型的预测是否与实际数据显著不同。
参数估计:判断某个参数是否对模型结果有显著影响。
比较不同模型:比较两种或多种模型在统计上是否有显著差异。
三种常用的统计检验方法
t检验(t-Test)
t检验是一种统计假设检验,用来确定两组数据之间是否存在显著差异。它主要有两种形式:
独立样本t检验(Independent Samples t-Test):用于比较两个独立样本组的平均值。例如,比较两个不同教学方法对学生成绩的影响。
配对样本t检验(Paired Samples t-Test):用于比较同一组受试者在两个不同条件下的表现。例如,比较同一组学生在接受不同教学方法前后的成绩变化。
t检验的核心是计算t值,这个值表示观测到的差异与随机差异之间的比例。然后,这个t值被用来确定p值,如果p值小于预先设定的显著性水平(通常是0.05),则认为两组之间存在显著差异。
方差分析(ANOVA)
ANOVA是一种用于比较三个或更多样本组平均值的统计方法。它主要分为:
单因素ANOVA(One-Way ANOVA):当我们只考虑一个因素时使用,例如,比较三种不同教学方法对学生成绩的影响。
多因素ANOVA(Factorial ANOVA):用于同时考虑两个或更多因素,例如,同时考虑教学方法和学生性别对成绩的影响。
ANOVA的核心是分析组内和组间的方差,以判断各组平均值之间是否存在显著差异。如果ANOVA的结果显著,通常会进行后续的多重比较测试(如Tukey测试),以确定哪些组别之间存在显著差异。
Kolmogorov-Smirnov检验(KS Test)
KS检验是一种非参数检验,用于比较一个样本或两个样本的累积分布函数(CDF)是否相同。它可以用于:
单样本KS检验:比较单个样本的分布是否符合特定的理论分布,例如正态分布或指数分布。
双样本KS检验:比较两个样本是否来自相同的分布。
KS检验的优点是它不需要假设数据遵循特定的分布(例如正态分布),使其在处理非正态分布的数据时特别有用。
习题7.1
1. 题目要求

2.解题过程
解:
(1)
首先,数学方法分析。
平均值和方差都未知的时候,灯泡寿命平均值 $ \mu $ 的置信度为0.90的置信区间为:
(
X
‾
−
S
n
t
α
/
2
(
n
−
1
)
,
X
‾
+
S
n
t
α
/
2
(
n
−
1
)
)
\left(\overline{{X}}\,-\,\frac{S}{\sqrt{n}}t_{\alpha/2}\left(\,n\,-\,1\,\right)\,,\overline{{X}}\,+\,\frac{S}{\sqrt{n}}t_{\alpha/2}\left(\,n\,-\,1\,\right)\,\right)
(X−nStα/2(n−1),X+nStα/2(n−1))
这里,其中:
1
−
α
=
0.9
,
α
=
0.1
,
α
/
2
=
0.05
,
n
=
5
,
n
−
1
=
4
1\,-\,\alpha=0.9\,,\alpha=0.1\,,\alpha/2=0.05\,,n=5\,,n\,-1=4
1−α=0.9,α=0.1,α/2=0.05,n=5,n−1=4
通过计算可以得到:
x
−
=
1
5
∑
i
=
1
5
x
i
=
1160
s
2
=
1
4
∑
i
=
1
4
(
x
i
−
x
‾
)
2
=
99.7484
\stackrel{-}{x}~=\;\frac{1}{5}\sum_{i=1}^{5}{x_{i}}~=~1160 \\ s^{2}\;=\;\frac{1}{4}\sum_{i=1}^{4}\;\;(\;x_{i}\,-\,\overline{{{x}}}\,)^{2}\;=\;99.7484
x− =51i=1∑5xi = 1160s2=41i=1∑4(xi−x)2=99.7484
接下来,通过代入公式,就可以求出置信区间(答案见后)。
(2)
其次,本题有着MATLAB专门的函数可以较为简便地求出结果。
在MATLAB中,ttest函数是进行单样本或双样本t检验的函数。t检验是一种常见的假设检验方法,用于比较两个样本的均值是否相等,或者一个样本的均值是否等于一个已知的值。
ttest函数的语法如下:
[h,p,ci,stats] = ttest(data,mu)
[h,p,ci,stats] = ttest(data1,data2)
其中,第一种情况是单样本t检验,第二种情况是双样本t检验。具体参数说明如下:
- data:需要进行t检验的数据样本,可以是一个向量或矩阵。
- mu:单样本t检验中的假设均值。
- data1、data2:双样本t检验中的两组数据样本,可以是向量或矩阵,但必须大小相同。
- h:表示是否拒绝原假设的逻辑值,1表示拒绝原假设,0表示不拒绝原假设。
- p:表示计算得到的p值,即原假设成立的概率。
- ci:表示置信区间,即均值的真实值有95%的可能在这个区间内。
- stats:包含检验统计量和自由度的结构体。
需要注意的是,ttest函数默认使用双侧检验,也就是假设均值不等于指定的值。如果需要使用单侧检验,可以通过设置alpha参数来实现。
本题,直接使用ttest函数即可解决。
3.程序
求解的MATLAB程序如下:
clc, clear
% 数据
age = [1050, 1100, 1120, 1250, 1280];
% 按照格式调用ttest函数
[h, p, ci, stats] = ttest(age, mean(age), 'Alpha', 0.1);
% ci就是置信区间
format long g
ci
4.结果

求出的总体均值的置信水平为0.90的置信区间为:(1064.90 , 1255.10)
习题7.2
1. 题目要求

2.解题过程
解:
这一题,决定采用柯尔莫哥洛夫(Kolmogorov-Smirnov) 检验的方法来做。
(1)
下面是数学方法分析:
假设
H
0
:
X
服从
N
(
μ
,
σ
2
)
H
1
:
X
不服从
N
(
μ
,
σ
2
)
H_0: X服从N(\mu,\sigma^{2}) \\ H_1: X不服从N(\mu,\sigma^{2})
H0:X服从N(μ,σ2)H1:X不服从N(μ,σ2)
由于题目中直接给出了均值和标准差,所以直接代入。
拒绝域为(其中n=50):
D
n
≥
1.36
n
D_{n}\geq{\frac{1.36}{\sqrt{n}}}
Dn≥n1.36
计算:
D
n
=
sup
x
i
∣
F
n
(
x
i
)
−
F
(
x
i
)
∣
D_n=\operatorname*{sup}_{x_{i}}\mid F_{n}(\,x_{i})\;-F(\,x_{i}\,)\;\mid
Dn=xisup∣Fn(xi)−F(xi)∣
如果最终计算结果不在拒绝域,则认为原假设成立。
(2)
其次,本题有着MATLAB专门的函数可以较为简便地求出结果。
KS检验(Kolmogorov-Smirnov Test)是一种非参数的假设检验方法,它用于检验一个样本是否符合特定的概率分布或者两个样本是否来自于同一分布。该方法可以用于连续或离散分布。
[h, p, ksstat] = kstest(x, y)
其中,x和y是要进行KS检验的两个样本数据(必须是向量),h是假设检验的结果,p是对应的P值,ksstat是KS统计量。
当h为1时,说明拒绝原假设,即两个样本不来自同一个分布或单个样本不来自指定分布;
当h为0时,说明不能拒绝原假设,即两个样本来自同一个分布或单个样本来自指定分布。
p值越小,说明越不可能两个样本来自同一个分布或单个样本来自指定分布。常用的显著性水平是0.05和0.01。如果p值小于显著性水平,就拒绝原假设。
ksstat是KS统计量,表示两个样本的最大差异。它的值越大,说明两个样本越不可能来自同一个分布或单个样本越不可能来自指定分布。
3.程序
求解的MATLAB程序如下:
clc, clear
diameters = [15.0, 15.8, 15.2, 15.1, 15.9, 14.7, 14.8, 15.5, 15.6, 15.3, ...
15.1, 15.3, 15.0, 15.6, 15.7, 14.8, 14.5, 14.2, 14.9, 14.9, ...
15.2, 15.0, 15.3, 15.6, 15.1, 14.9, 14.2, 14.6, 15.8, 15.2, ...
15.9, 15.2, 15.0, 14.9, 14.8, 14.5, 15.1, 15.5, 15.5, 15.1, ...
15.1, 15.0, 15.3, 14.7, 14.5, 15.5, 15.0, 14.7, 14.6, 14.2, ...
];
% 柯尔莫哥洛夫(Kolmogorov-Smirnov) 检验
pd = makedist('Normal', 'mu', 15.0780, 'sigma', 0.4325);
[h, p, st] = kstest(diameters, 'CDF', pd);
% 展示结果
h
p
st
% 画图展示
cdfplot(diameters)
hold on
x_values = linspace(min(diameters), max(diameters));
plot(x_values, normcdf(x_values, 15.0780, 0.4325), 'r-')
legend('Empirical CDF', 'Normal CDF', 'Location', 'best')
4.结果

在结果中,我们可以看到,h的值为0,所以我们可以认为题目中的数据是服从题目中所给出的正态分布的。

同时,还将经验累积分布函数和正态分布的累积分布函数绘制在同一个图形中,以便进行比较和分析。经过直观比较也可以看出数据服从正态分布。这与上面的kstest函数的计算结果相符合。
习题7.4
1. 题目要求

2.解题过程
解:
原假设
H
0
:
μ
1
=
μ
2
=
μ
3
H
1
:
μ
1
,
μ
2
,
μ
3
不全相等
H_{0}:\mu_{1}=\mu_{2}=\mu_{3} \\ H_{1}:\mu_{1},\mu_{2},\mu_{3}不全相等
H0:μ1=μ2=μ3H1:μ1,μ2,μ3不全相等
如果H0为真:
F
=
(
n
−
s
)
S
A
(
s
−
1
)
S
E
∼
F
(
s
−
1
,
n
−
s
)
F=\frac{\left(\,n\,-s\,\right)S_{A}}{\left(\,s\,-\,1\,\right)S_{E}}\sim F\left(\,s\,-\,1\,,n\,-\,s\,\right)
F=(s−1)SE(n−s)SA∼F(s−1,n−s)
拒绝域为
F
>
F
α
(
s
−
1
,
n
−
3
)
=
F
α
(
2
,
12
)
=
3.8853
F>F_{\alpha}(s-1\,,n-3\,)=F_{\alpha}(2\,,12\,)=3.8853
F>Fα(s−1,n−3)=Fα(2,12)=3.8853
下面,直接使用anova1函数就可以解决问题。
3.程序
求解的MATLAB程序如下:
clc, clear
a = [98, 93, 103, 92, 110; ...
100, 108, 118, 99, 111; ...
129, 140, 108, 105, 116];
% 方差分析
[p,t,st] = anova1(a'); % 注意这里要转置一下
% 展示结果
p
t
st
F = t{2,5}
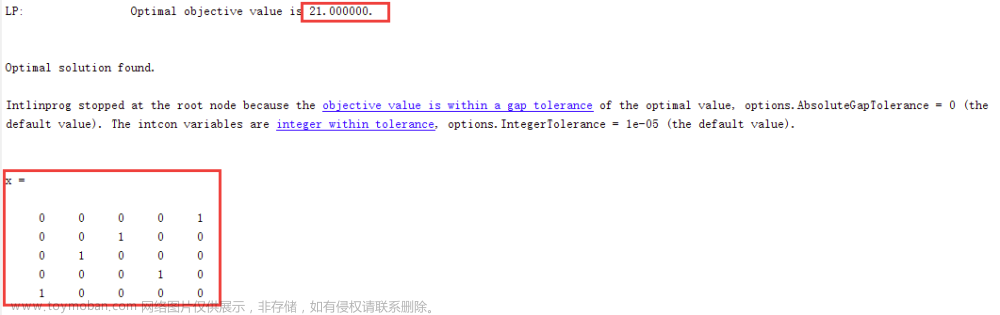
4.结果


通过上面的结果,我们可以看出:
S
A
=
1056.53
S
E
=
1338.8
F
=
4.7350
S_A=1056.53\\S_E=1338.8\\F=4.7350
SA=1056.53SE=1338.8F=4.7350
结果在拒绝域当中,所以认为,理赔额均值存在显著差异。文章来源:https://www.toymoban.com/news/detail-775144.html
如果这篇文章对你有帮助,欢迎点赞与收藏~文章来源地址https://www.toymoban.com/news/detail-775144.html
到了这里,关于【数学建模】《实战数学建模:例题与讲解》第六讲-假设检验(含Matlab代码)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!