TSP问题的遗传算法实现-Toy模板网

这篇具有很好参考价值的文章主要介绍了TSP问题的遗传算法实现。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一.实验目的

本实验课程是计算机、智能、物联网等专业学生的一门专业课程，通过实验，帮助学生更好地掌握人工智能相关概念、技术、原理、应用等；通过实验提高学生编写实验报告、总结实验结果的能力；使学生对智能程序、智能算法等有比较深入的认识。要掌握的知识点如下：

掌握人工智能中涉及的相关概念、算法；

熟悉人工智能中的知识表示方法；

掌握问题表示、求解及编程实现；

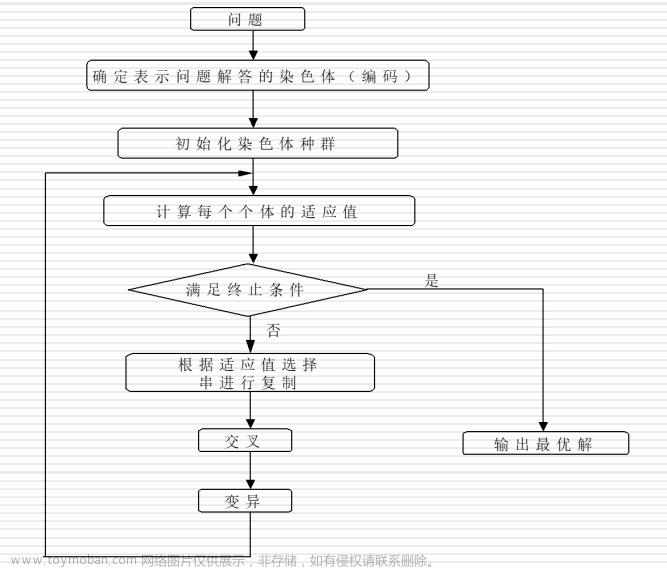
熟悉和掌握遗传算法的基本概念和基本思想；

理解和掌握遗传算法的各个操作算子，能够用选定的编程语言设计简单的遗传优化系统；

通过实验培养学生利用遗传算法进行问题求解的基本技能。

二.实验内容：

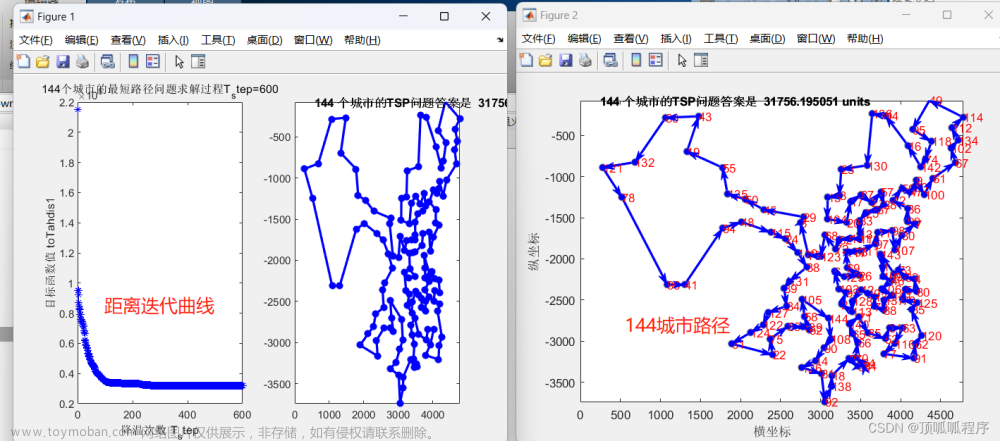
以N个节点的TSP（旅行商问题）问题为例，应用遗传算法进行求解，求出问题的最优解。

1 旅行商问题

旅行商问题（Traveling Salesman Problem, TSP），又译为旅行推销员问题、货担郎问题，简称为TSP问题，是最基本的路线问题。假设有n个可直达的城市，一销售商从其中的某一城市出发，不重复地走完其余n-1个城市并回到原出发点，在所有可能的路径中求出路径长度最短的一条。

TSP问题是组合数学中一个古老而又困难的问题，也是一个典型的组合优化问题，现已归入NP完备问题类。NP问题用穷举法不能在有效时间内求解，所以只能使用启发式搜索。遗传算法是求解此类问题比较实用、有效的方法之一。

下面给出30个城市的位置信息：

表1 Oliver TSP问题的30个城市位置坐标

城市编号	坐标	城市编号	坐标	城市编号	坐标
1	(87，7)	11	(58，69)	21	(4，50)
2	(91，38)	12	(54，62)	22	(13，40)
3	(83，46)	13	(51，67)	23	(18，40)
4	(71，44)	14	(37，84)	24	(24，42)
5	(64，60)	15	(41，94)	25	(25，38)
6	(68，58)	16	(2，99)	26	(41，26)
7	(83，69)	17	(7，64)	27	(45，21)
8	(87，76)	18	(22，60)	28	(44，35)
9	(74，78)	19	(25，62)	29	(58，35)
10	(71，71)	20	(18，54)	30	(62，32)

最优路径为：1 2 3 4 6 5 7 89 10 11 12 13 14 15 16 17 19 18 20 21 22 23 24 25 28 26 27 29 30

其路径长度为：424.869292

也可取前10个城市的坐标进行测试：

表2 Oliver TSP问题的10个城市位置坐标

城市编号	坐标
1	(87，7)
2	(91，38)
3	(83，46)
4	(71，44)
5	(64，60)
6	(68，58)
7	(83，69)
8	(87，76)
9	(74，78)
10	(71，71)

有人求得的最优路径为： 0 3 5 4 9 8 7 6 2 1 0

路径长度是166.541336

上述10个城市的求解中编号从0开始，把所有路径搜索完又返回到出发节点。

2 问题描述

应用遗传算法求解30/10个节点的TSP（旅行商问题）问题，求问题的最优解。

三.算法思路：

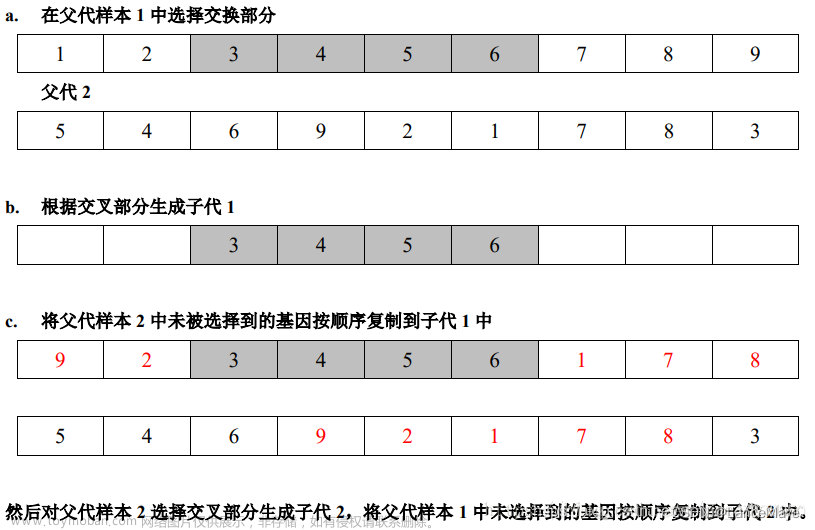
利用遗传算法解决tsp问题。

遗传算法：求十个点之间最短路径（包括最后回到起点）

yichuan(indata:list,data:list):

1.得到十个点

2.10个点随机排序变成8个排序组合

3.分别4次抽一个出来基因突变，4次抽两个出来对其中一个基因交换

4.两个八个进行按照大小适合度的排序，若新的对应那个比旧的对应的小，则交换。

5.重复直到连续n次最小适合度值不变，输出最小适合度对应路径。

基因突变：

1.选择出一个路径的排列组合

2.随机选择其中连续的k个路径点进行改变顺序

基因交换：

对其中一个排列组合选择其中k个连续点。

把这连续的k个点在另一个排列组合中删掉。

在这k个连续的点连续地加入到被删掉这几个点的排列组合中。

四.代码：

读取每个点坐标：

data.txt：坐标可以更多维度，data.txt里面设置坐标即可。

目前为：点编号，x，y

1,87,7
2,91,38
3,83,46
4,71,44
5,64,60
6,68,58
7,83,69
8,87,76
9,74,78
10,71,71
11,58,69
12,54,62
13,51,67
14,37,84
15,41,94
16,2,99
17,7,64
18,22,60
19,25,62
20,18,54
21,4,50
22,13,40
23,18,40
24,24,42
25,25,38
26,41,26
27,45,21
28,44,35
29,58,35
30,62,32

main.py:文章来源地址https://www.toymoban.com/news/detail-775179.html

import random
import copy

def openreadtxt(file_name):
    data = []
    file = open(file_name, 'r', encoding='utf-8')  # 打开文件
    file_data = file.readlines()  # 读取所有行
    for row in file_data:
        tmp_list = row.split(',')  # 按‘，'切分每行的数据
        tmp_list[-1] = tmp_list[-1].replace('\n', '')  # 去掉换行符
        data.append(tmp_list)  # 将每行数据插入data中
    return data


def indata(data):
    indata = []
    print('请输入10个城市编号，从1-',data[-1][0],'，计算机将求出最小距离：')
    for i in range(0, 10):
        print('请输入第', (i + 1), '个编号：')
        theindata = int(input())
        while 1:
            if theindata not in range(1, 31) or theindata in indata:
                print('输入数据范围错误或者已存在于data中，请重新输入：')
                theindata = int(input())
            else:
                break
        indata.append(theindata)
    return indata


# def kernalfind(data_xiabiao, data: list):#return可能有问题
#     for idata in range(len(data)):
#         if data[idata][0] == data_xiabiao:
#             return idata


def sorttsp(datas: list, data: list):
    data_value = []
    begin_data = 0
    thelen = len(data[0])

    #添加头部点，以计算结尾回去的距离
    for datas_data in datas:
        datas_data.append(datas_data[0])

    for thedatas in datas:  # 从8列数据里面拿出1列数据
        thevalue = 0  # 计算10+1个点的距离
        for thedata in thedatas:  # 计算10+1个点的距离之和
            iivalue = 0  # 计算两点间距离
            if thedata == thedatas[0]:
                begin_data = thedata
            else:
                #begin_data = kernalfind(begin_data, data)
                #thedata_1 = kernalfind(thedata, data)
                begin_data=int(begin_data)-1
                thedata_1 = int(thedata) - 1
                for ii in range(1, thelen):
                    iivalue = iivalue + (int(data[begin_data][ii]) - int(data[thedata_1][ii])) ** 2
                thevalue = thevalue + iivalue ** (1 / 2)
                begin_data = thedata
        data_value.append(thevalue)

    #去除最后的节点，恢复原状
    for datas_data in datas:
        datas_data.pop()

    return data_value


def value_data(datas_v: list, datas: list, ):
    for data in range(len(datas)):
        datas[data].append(datas_v[data])
    return datas


'''
yichuan(indata:list,data:list):
1.得到十个点
2.10个点随机排序变成8个排序组合
3.分别4次抽一个出来基因突变，4次抽两个出来对其中一个基因交换
4.两个八个进行按照大小适合度的排序，若新的对应那个比旧的对应的小，则交换。
5.重复直到连续10次最小适合度值不变，输出最小适合度对应路径。
'''


def yichuan(indata: list, data: list):
    all_value=[]#存放所有value
    all_road=[]#存放所有路径
    i = 0  # 连续20次最小适合度值不变结束
    i_i = 0  # 计算最小适合度下标
    i_i_value=0#存放最终最小value
    datas_1 = []  # 存放旧随机8个排序组合
    for ii in range(0, 8):  # 得到8个排序组合
        indata = copy.deepcopy(indata)#防止改变datas_1里面的元素
        random.shuffle(indata)
        while 1:
            if indata in datas_1:
                indata = copy.deepcopy(indata)#值和id都一样
                random.shuffle(indata)
            else:
                datas_1.append(indata)
                break
    while i < 20:#可以改变，然后就可以让更多次最小适合度不变才结束。
        print('开始一次,i=',i)
        datas_2 = []  # 存放新随机8个排序组合

        # for ii in range(0, 8):  # 得到8个排序组合
        #     random.shuffle(indata)
        #     indata = copy.deepcopy(indata)
        #     while 1:
        #         if indata in datas_1:
        #             indata = copy.deepcopy(data)
        #         else:
        #             datas_1.append(indata)
        #             break

        # --------------------基因突变-----------------------------------

        # 4次抽一个出来基因突变
        xs = []#存放要进行基因突变的4个排列组合
        for iii in range(0, 4):  # 找到8个里面要抽出来的4个
            # random.randint(0, 7)#(1,10)==[1,10]而不是[1,10)
            while 1:  # 要4个不重复的数字
                x1 = random.randint(0, 7)
                if x1 not in xs:
                    xs.append(x1)
                    break

        # 对四个数据进行基因突变
        for i1 in xs:  # xs里面是4个下标,找到每个下标
            x2 = random.randint(0, 7)  # 找到下标，进行3个元素的随机变化
            new_data = copy.deepcopy(datas_1[i1])
            x3 = []#存放要基因突变的3个元素
            x3.append(datas_1[i1][x2])
            x3.append(datas_1[i1][x2 + 1])
            x3.append(datas_1[i1][x2 + 2])
            random.shuffle(x3)
            new_data[x2] = x3[0]
            new_data[x2 + 1] = x3[1]
            new_data[x2 + 2] = x3[2]
            # new_data为这行数据突变完的结果
            datas_2.append(new_data)

        # --------------------基因交换-----------------------------------

        # 再对其中四个数据进行基因交换
        xs = []
        for iii in range(0, 4):  # 找到要抽出来的四个
            # random.randint(0, 7)#(1,10)==[1,10]而不是[1,10)
            while 1:  # 要4个不重复的数字
                x1 = random.randint(0, 7)
                if x1 not in xs:
                    xs.append(x1)
                    break
        for i1 in xs:  # xs里面是4个下标,找到每个下标
            x1 = 0
            #new_data=copy.deepcopy(new_data)
            new_data = copy.deepcopy(datas_1[i1])

            while 1:  # 要1个不与重复i的数字
                x1 = random.randint(0, 7)#8列里面选出一个不等于i的那一列数据
                if x1 != i1:
                    break
            # i和x1是两个数据的下标，对这两个数据进行基因交换

            x2 = random.randint(0, 7)#10个数据里面随机选出3个连续的数据的起点
            ii = x2
            while ii != x2 + 3:
                new_data.remove(datas_1[x1][ii])
                ii = ii + 1
            new_data.append(datas_1[x1][x2])
            new_data.append(datas_1[x1][x2 + 1])
            new_data.append(datas_1[x1][x2 + 2])
            datas_2.append(new_data)
        # 现在有八个新数据了
        # -------------两个八个进行按照大小适合度的排序，若新的对应那个比旧的对应的小，则交换。---------------------------------------------
        # datas_1 = []#存放旧随机8个排序组合         datas_2=[]#存放新随机8个排序组合
        datas_1v = sorttsp(datas_1,data)
        datas_2v = sorttsp(datas_2,data)
        datas_1 = value_data(datas_1v, datas_1)
        datas_2 = value_data(datas_2v, datas_2)
        datas_1v.sort()
        datas_2v.sort()

        for ii in range(len(datas_1v)):
            if ii == 0:#记录每次最优路径
                if datas_1v[ii] <= datas_2v[ii]:
                    #判断是否为第一次比较，防止数据未被放入all_raod或者all_value中
                    if datas_1v[ii] not in all_value:
                        all_value.append(datas_1v[ii])
                        for iii in datas_1:
                            if iii[-1]==datas_1v[ii]:
                                all_road.append(iii)

                    i = i + 1
                else:#datas_1v[ii] > datas_2v[ii]
                    all_value.append(datas_2v[ii])
                    for iii in datas_2:
                        if iii[-1] == datas_2v[ii]:
                            all_road.append(iii)
                    i = 0
            if ii == 0 and i == 10:
                for iii in range(len(datas_1)):
                    if datas_1[iii][-1] == datas_1v[ii]:
                        i_i = iii
                        i_i_value=datas_1v[ii]
            if datas_1v[ii] > datas_2v[ii]:  # 旧的>新的
                for iii in range(len(datas_1)):
                    if datas_1[iii][-1] == datas_1v[ii]:#是datas_1[iii][-1] == datas_1v[ii]，而不是datas_1[iii][-1] == datas_2v[ii]
                        for iiii in range(len(datas_2)):#注意逻辑，要旧值对应的行=新值对应的行
                            if datas_2[iiii][-1] == datas_2v[ii]:
                                datas_1[iii]=datas_2[iiii]

        for ii in range(len(datas_1)):
            datas_1[ii].remove(datas_1[ii][-1])
    # ------------结束全部工作，输出最优排序-------------------------------------------------------
    #all_value = []  # 存放所有value
    #all_road = []  # 存放所有路径
    for i_r_v in range(0,len(all_value)):
        print('局部最优路径和值：',all_road[i_r_v],'到起点',all_road[i_r_v][0])
        print('局部最优路径值：',all_value[i_r_v])
    print('----------------最终最优路径和值：----------------------------------------')
    print(datas_1[i_i],'到起点',datas_1[i_i][0],'value=',i_i_value)

#变量名要起好，不然重复会导致错误
if __name__ == "__main__":
    data = openreadtxt('data.txt')#读取全部点坐标
    indata = indata(data)#选择点路径
    yichuan(indata, data)#遗传算法

到了这里，关于TSP问题的遗传算法实现的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！