目录
前言
实验要求
算法描述
个人想法
代码实现和思路、知识点讲解
知识点讲解
文件传输
Huffman树的存储
Huffman的构造
Huffman编码
编码和译码
代码实现
文件写入和输出
Huffman树初始化
构造Huffman树
求带权路径长度
Huffman编码
Huffman译码
结束
代码测试
测试结果
前言
实验要求
利用Huffman编码进行通信可以大大提高信道利用率,缩短信息传输时间,降低传输成本。试为这样的信息收发站编写一个Huffman的编/译码系统。给定一组权值 {7,9,5,6,10,1,13,15,4,8},构造一棵赫夫曼树,并计算带权路径长度WPL。
算法描述
1.初始化:从键盘读入n个字符,以及它们的权值,建立Huffman树。
2.编码: 根据建立的Huffman树,求每个字符的Huffman编码。对给定的待编码字符序列进行编码。
3.译码: 利用已经建立好的Huffman树,对上面的编码结果译码。
译码的过程是分解电文中的字符串,从根结点出发,按字符‘0’和‘1’确定找左孩子或右孩子,直至叶结点,便求得该子串相应的字符。具体算法留给读者完
个人想法
这一期是完成最最最基本要求的Huffman树的创建和编码译码。越是深入学习,越会发现很多的需求和案例都是在身边的,脱离应用,单纯就写一个算法的实现感觉还是不那么能感受到学习的快乐,所以我后面还会有进阶版本的。
代码实现和思路、知识点讲解
知识点讲解
文件传输
我在写代码的时候一个是在进行代码调试和效果测试的时候觉得频繁输入数据去调试很麻烦,另一方面是在问题描述中也说了,利用Huffman编码进行通信,那如果抛开文件的,数据的传输,那就是空谈了,所以我们第一步就是文件的读取和写入。
Huffman树的存储
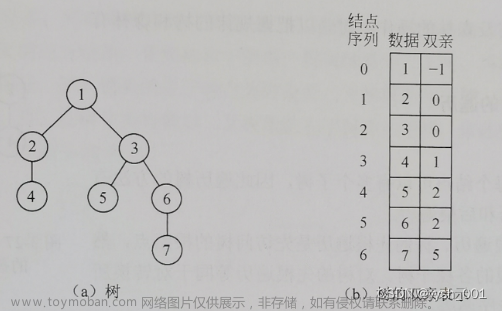
有了数据来源,下一步就是确定树在内存中的存储,我们先来用顺序结构,链式结构我后面也会出的。结构体定义:
typedef struct {
char data;
unsigned int weight; //不为0
unsigned int parent; //头结点没有双亲用来存叶子结点数量
unsigned int lChild, rChild;
} HTNode, *HTree;
这里用的全部都是unsigned int型,就是无符号整型,计算机存储是没有符号的,拿了一半无符号数的空间补码存储负数,无符号数就是把这段空间拿回来,全部存正数。
Huffman的构造
我觉得相对而言这是最难的部分,主要是代码方面可能会有些绕。知道存储,要构造Huffman数就要先找到什么是哈夫曼树又是怎么构建的。


可以看到,最开是全是叶子结点,选择权值最小的两结点构成一个小树,小树的根节点继续参与选择,选两个最小的结点构成树,特别注意,不是只能存在一棵树,可能会同时存在好几颗树,而不是盯着一只羊毛薅。最后效果如下:

Huffman编码
其实不过就是大一点的二叉树,看到图,那Huffman编码就很简单了,因为计算机是01二进制,二叉树也是只有左右两个子树,那就可以得到各个叶子结点的编码了

可以发现,如果在每一个岔路口,也就是每一个层次上标注清楚,左拐是0,右拐是1,那对应的编码自然就出来了,例如:15对应的是01;4对应的是10011;这就是Huffman编码。
编码和译码
每个叶子结点的权可以看作他们的出现频率,频率越高,就要摆在越容易够到的地方,那我们可以将一篇文章所有出现的字符都看作一个叶子结点,而它出现的次数就是它的权,权越大离根节点就越接近。
编码就是将这些字符作为叶子结点构成Huffman树,用Huffman的01编码表示,例如我要表示9和7就是0001011;译码就是根据01从Huffman树的根节点开始,直到找到叶子结点,翻译为一个字符。
代码实现
文件写入和输出
文件写入和输出就是靠指针实现,我喜欢读写分开来,定义w为只写,r为只读,a为追加,简单展示一下:
//读取文件并存初始化哈夫曼树
HTree ReadFile() {
FILE * fp = fopen(Fname, "r"); //只读方式打开
printf("----------正在读取文件----------\n\n");
int n;
char cf, cs;
fscanf(fp, "%d %c", &n, &cs); //读取第一个数据为哈夫曼树叶子结点数量
HTree ht = (HTree)malloc((2*n-1)*sizeof(HTNode));
if (!ht) {
printf("!!!malloc Error!!!\n");
exit(1);
}
int i;
for (i = 0; i < 2*n-1; i++) {
ht[i].weight = ht[i].parent = ht[i].lChild = ht[i].rChild = 0;
ht[i].data = '#';
}
ht[0].parent = n;
i = 1;
do {
fscanf(fp, " %c %c", &(ht[i].data), &cf);
fscanf(fp, " %u %c", &(ht[i].weight), &cs);
i++;
} while (cf == ',' && cs == ';'); //'#'结束
fclose(fp);
if (cf != ',' || cs != '#') {
printf("!!!File Error!!!\n");
exit(1);
}
printf("----------文件读取完成----------\n\n");
return ht;
}我写好了一个文件,一个字符是数量,剩下的就是对应结点元素和权值:

从上面的方法可以看到,文件的方法和c语言的一般方法差不多,scanf从键盘获取,fscanf就是从文件获取,除了多了一个指针fp,其他格式一模一样。
Huffman树初始化
上面代码,我除了读取文件信息外,我还将Huffman树初始化。n个叶子结点,Huffman树就有2*n-1个节点所以我们开2*n-1个空间就行。大家的习惯是喜欢把根节点放在最后一个,但是我个人更喜欢把根节点放在第一个,因为需要的时候一下子就可以找到,而且根节点没有双亲,那完全可以子啊根节点的双亲里面存储叶子节点个数。我将根节点存在第0单元,1-n单元分别存放1-n个元素。
构造Huffman树
因为我将根节点放在第1单元内,所以我和书上的代码有些不一样,但是大同小异,我对这个方法做出了优化后面会单独出一篇博客:
//构造哈夫曼树
HTree CreateHTree() {
HTree ht = ReadFile();
int n = ht[0].parent; //头结点没有双亲用来存叶子结点数量
int i;
for (i = n + 1; i < 2 * n; i++) {
int j = 0, lNode, rNode;
unsigned int min1, min2 = -1;
while (ht[++j].parent); //找到第一个未分配的结点
min1 = ht[j].weight;
lNode = j;
while (++j < i) {
if (!ht[j].parent) {
if (ht[j].weight < min1) {
min2 = min1;
rNode = lNode;
min1 = ht[j].weight;
lNode = j;
}
else if (ht[j].weight < min2) {
min2 = ht[j].weight;
rNode = j;
}
}
}
if (min1 + min2 < min1 || min1 + min2 < min2) {
printf("!!!Error Overflow!!!\n");
exit(1);
}
j = j % (2 * n - 1);
ht[j].weight = min1 + min2;
ht[j].lChild = lNode;
ht[j].rChild = rNode;
ht[lNode].parent = j;
ht[rNode].parent = j;
}
printf("----------哈夫曼树构建成功----------\n");
return ht;
}其实本质上就是选择排序,选择排序是选出一个最小或最大的,这个只要加一个变量记录次小的就和选择排序一模一样了。找到之后将权值,孩子,双亲等值赋好就ok。
求带权路径长度
我们学了递归,抱着递归的思想去做这题就会非常简单:
//定义递归函数,计算带权路径长度
int getWPL(HTree ht, int index, int depth) {
//如果是叶子结点,返回WPL
if (!ht[index].lChild && !ht[index].rChild) {
return ht[index].weight * depth;
}
else { //如果不是叶子结点,递归遍历其左右子树,深度加1
return getWPL(ht, ht[index].lChild, depth+1) + getWPL(ht, ht[index].rChild, depth+1);
}
}一个if else语句,加上两个return解决。
Huffman编码
这里为了让元素和编码之间联系更加紧密,我单独定义一个结构体来存储,就一个字符加一个数组。
//哈夫曼树编码存储
typedef struct {
char data;
char *cd;
} HCode;
//创建哈夫曼树编码
HCode *CreateHCode(HTree ht) {
int n = ht[0].parent;
HCode *hc = (HCode *)malloc(n * sizeof(HCode));//存放哈夫曼编码
char *code = (char *)malloc(n * sizeof(char)); //存放临时编码
code[n-1] = '\0'; //编码结束符
int i;
for (i = 1; i < n + 1; i++) { //遍历每个叶子结点
hc[i-1].data = ht[i].data;
int start = n - 1; //编码起始位置
int c = i; //当前结点下标
int p = ht[i].parent; //父节点下标
while (c != 0) { //直到根节点
if (ht[p].lChild == c) { //左孩子为0
code[--start] = '0';
}
else { //右孩子为1
code[--start] = '1';
}
c = p; //移动到父节点
p = ht[p].parent; //移动到祖父节点
}
hc[i-1].cd = (char *)malloc((n - start) * sizeof(char));
strcpy(hc[i-1].cd, &code[start]);
}
free(code);
printf("\n----------哈夫曼树编码成功----------\n");
return hc;
}哈夫曼树编码需要注意的一个点就是,我们从根节点很难明确到叶子节点的路径,但是我们从叶子节点可以唯一确定一条路走向根节点,因为树的性质可以有很多孩子但是只能有一个双亲。所以大家在求编码的时候要从叶子节点开始倒着求。我推荐大家使用栈,后进先出的性质在这里简直不要太好用,我是偷了个懒直接从字符串末尾往前求,然后用字符串函数的赋值方法。
Huffman译码
知道了什么是编码,那么译码简直不要太简单
//哈夫曼树译码
void DeHCode(HTree ht, char *code) {
int k = 0; //当前节点下标
int i;
for (i = 0; code[i] != '\0'; i++) { //遍历序列中的每个字符
if (code[i] == '0') { //向左走
k = ht[k].lChild;
}
else if (code[i] == '1') { //向右走
k = ht[k].rChild;
}
else { //非法字符
printf("!!!Invalid Code Error!!!\n");
exit(1);
}
if (ht[k].lChild == 0 && ht[k].rChild == 0) { // 到达叶子节点
printf("%c", ht[k].data); // 输出对应字符
k = 0; // 返回根节点继续遍历
}
}
printf("\n");
}你只需要跟着01的指引访问左节点或者右节点,直到遇到叶子节点,输出元素并回溯到根节点。周而复始直到访问完所有元素。
结束
代码测试
我写个主调函数测试代码
int main() {
printf("%s\n", Fname);
HTree ht = CreateHTree();
printf("哈夫曼树的带权路径长为:%d\n", getWPL(ht, 0, 0));
HCode *hc = CreateHCode(ht);
printf("字符\t编码\n");
int i;
for (i = 0; i < ht[0].parent; i++) {
printf("%c\t%s\n", hc[i].data, hc[i].cd);
}
char *c = "001000100101011111010110101110101110";
printf("\n%s\n译码后为:", c);
DeHCode(ht, c);
printf("\n----------测试结束----------\n");
return 0;
}测试结果
 文章来源:https://www.toymoban.com/news/detail-775446.html
文章来源:https://www.toymoban.com/news/detail-775446.html
文章来源地址https://www.toymoban.com/news/detail-775446.html
到了这里,关于数据结构 实验17:Huffman树和Huffman编码——学习理解哈夫曼树的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!