数据结构---最小生成树（(普里姆算法)C语言看了就懂教程）-Toy模板网

这篇具有很好参考价值的文章主要介绍了数据结构---最小生成树（(普里姆算法)C语言看了就懂教程）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1.概述

普里姆算法就是“加点法”，是一种将连通网转换成最小生成树的一种算法

在一个连通图的所有生成树中，各边代价之和最小的那颗生成树称为该连通图的最小代价生成树（MST）

2.算法逻辑：

①对于任意一张连通图，假设 N = (V,E)是连通网，TE就是最小生成树中边的集合

②生成树先从一个结点开始，U = {u0}，u0就是V中的任意一点。

③在V-U中所有的(u,v)中找出最短一条边，并入TE中

④循环往复第三步就能得到最小生成树 (V,TE)---(顶点，边)

3.上述算法逻辑就是课本上的算法描述，更通俗易懂的理解如下

普里姆算法（贪心算法）

步骤：

①先将图拆解成森林

②以任意一个顶点为出发点，通过对到其他顶点的权值进行比较，找到最小边得到一颗树(顶点，边)集合

③将②中的”顶点“换成“这颗树”与其他顶点是否有更小的权值

④重复第③步就可以得到最小生成树

使用实例：

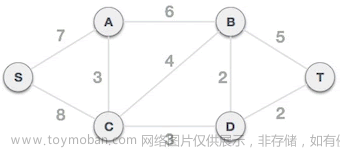
对于最小生成树的概念，可以拿生活中的地图来进行说明

eg：假设每个城市之间都有固定的路径，固定的距离，这是就可以将其理解成一张很大的无向图，当需要去建造铁路网，得考虑到材料资金问题，时间问题，效率问题等等。。。

就是要找到连通城市网络所需要付出的最小代价的方法，就需要将城市网转换成最小生成树。

4.代码框架讲解

如何去实现一个工程或者算法的代码，需要哪些对象(函数变量)，首先的清楚需要什么功能(函数方法)，实现逻辑(上述已经讲了)

需要哪些对象(函数变量)？

既然是连通图就得有图的数据类型

     typedef struct
     {
           char vexs[MAXVEX];          //顶点表
           int arc[MAXVEX][MAXVEX];    //边表
           int numVertexes,numEdges;   //顶点数量
           int GraphType;              //图的类型
     }MGraph;

既然比较子连通图中边的权值，得有存放的地方

        struct fuzhu                         //辅助数组---说到底就是算法的本质
        {
            char adjvex;                    //权值
            int lowcost;                    //坐标点
        };

        struct fuzhu closedge[MVNum];   //定义辅助队列结构体

以上两个结构体就是主要的变量类型，其他的int、char之类的都是辅助性的

需要什么功能(函数方法)？

围绕算法，你需要创建一张连通图

        void CreateMGraph(MGraph *G)                //创建图列

打印出连通图

        void output(MGraph *G)                      //输出

需要去找权值集合中的最小值

        int Min(MGraph *G)                          //获取辅助队列中，权值集合中最小的权值

因为是从任意一点开始就得先知道其顶点坐标

        int LocateVex(MGraph *G,char u)             //获取图表中顶点为u的顶点

算法实现，传入任意连通图跟随机顶点，生成最小树

 void MiniMGraph_prim (MGraph *G, char u)    //选择从哪个顶点开始，随机就行没有针对性说要哪个

5.代码具体实现以及讲解

本文只讲解对于辅助数组的用法实现，以及MiniMgraph_prim()的实现

辅助数组其实就是个很简单的结构体而已，主要是你得知道如何去用，

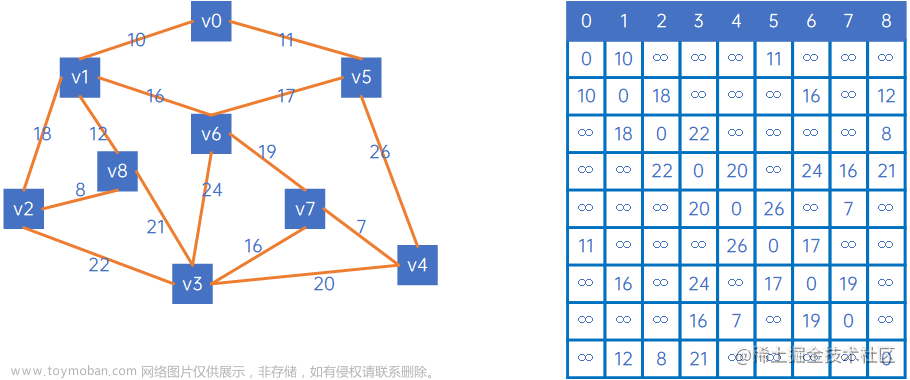
因为在创建连通图的生成过程中，两结点之间要么为权值要么就为65535，利用这点实现算法中枢。

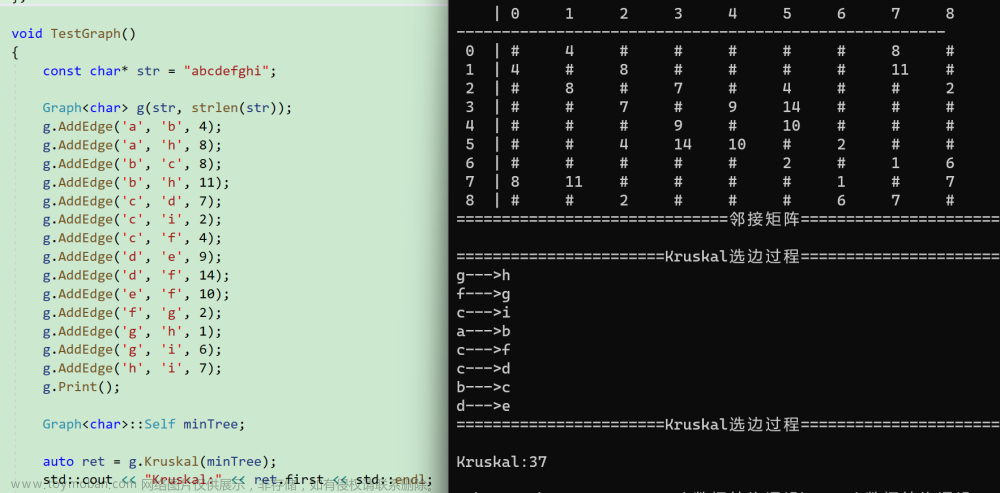
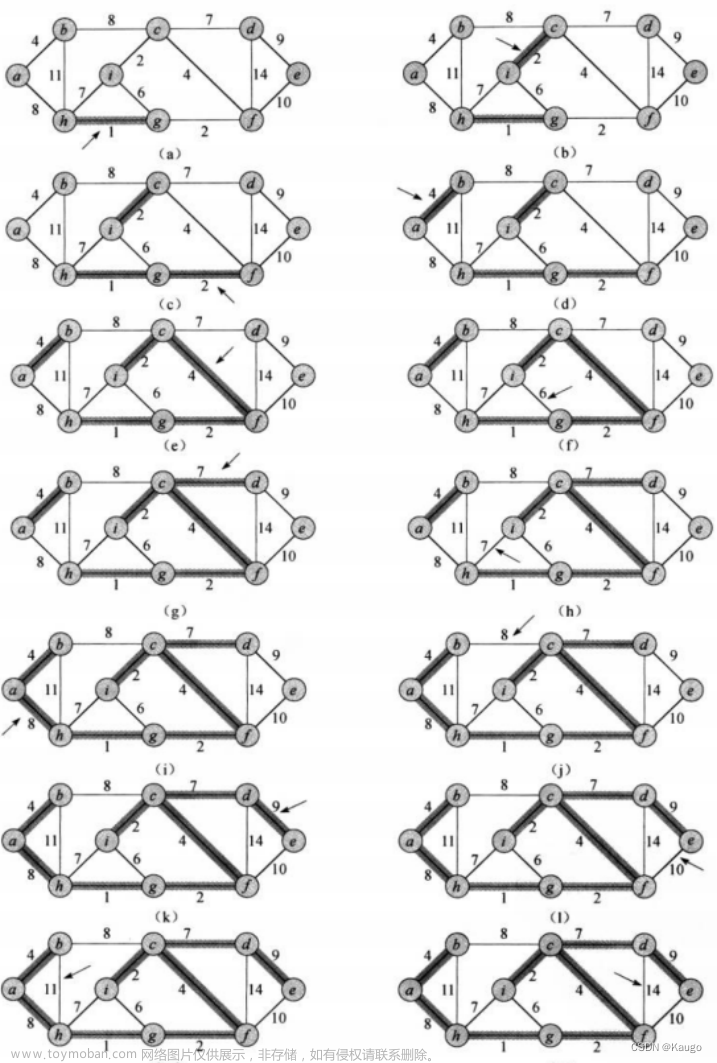
文字难讲清楚，而且难看，直接看图解

山东大学数据结构实验最小生成树prim算法c语言,算法,数据结构,c语言,贪心算法

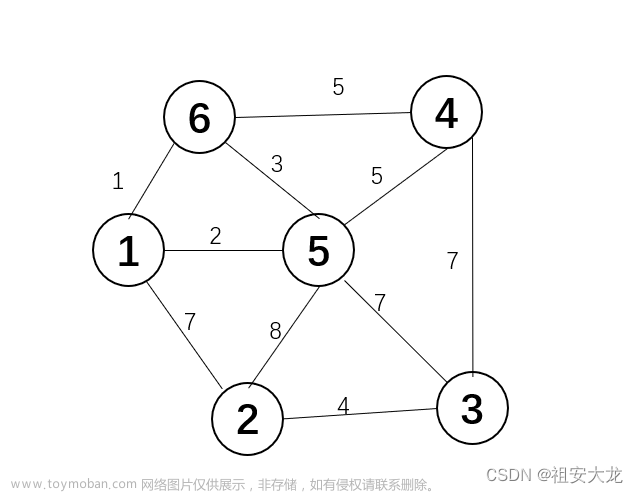
创建一个新的图列---无向连通图

山东大学数据结构实验最小生成树prim算法c语言,算法,数据结构,c语言,贪心算法

prim算法实现步骤

山东大学数据结构实验最小生成树prim算法c语言,算法,数据结构,c语言,贪心算法

辅助数组元素变化

        void MiniMGraph_prim (MGraph *G, char u)    //选择从哪个顶点开始，随机就行没有针对性说要哪个
        {
            int k;
            char u0,v0;
            int  j,i;
            k = LocateVex(G,u);
            for(j = 0;j<G->numVertexes;j++)
            if(j != k)  
            {
                closedge[j]. adjvex = u;
                closedge[j].lowcost = G->arc[k][j];
            }
            closedge[k].lowcost = 0;
            //初始化辅助结构体，将其边上的权值添加进结构体
            for(i = 1;i<G->numVertexes;i++)
            {
                k = Min(G);
                u0 = closedge[k].adjvex;
                v0 = G->vexs[k];
                printf("%c %c\n",u0,v0);
                closedge[k].lowcost = 0;
                for(j =0;j<G->numVertexes;j++)
                    if(G->arc[k][j]<closedge[j].lowcost)
                    {
                        closedge[j].adjvex = G->vexs[k];
                        closedge[j].lowcost = G->arc[k][j];
                    }          
            }
            /*
            从各组边closedge中选出最小边，并输出此边
            再判断该最小边上是否有更小的边，若有则将其顶点和权值都添加进结构体
            如此反复 就能得到最小生成树
            */
        }

上述MiniMGraph_prim()中：

首先找出随机顶点的坐标值以及将辅助数组进行初始化(初始化的过程就是对应辅助数列的第一步)

            k = LocateVex(G,u);
            for(j = 0;j<G->numVertexes;j++)
            if(j != k)  
            {
                closedge[j]. adjvex = u;
                closedge[j].lowcost = G->arc[k][j];
            }
            closedge[k].lowcost = 0;
            //初始化辅助结构体，将其边上的权值添加进结构体

①找出辅助数组最小权值的下标k，并将其(u0)adjvex和v0(G->vex[k])打印；

            k = Min(G);
            u0 = closedge[k].adjvex;
            v0 = G->vexs[k];
            printf("%c %c\n",u0,v0);

②更新辅助数组；

            for(j =0;j<G->numVertexes;j++)
                if(G->arc[k][j]<closedge[j].lowcost)
                {
                    closedge[j].adjvex = G->vexs[k];
                    closedge[j].lowcost = G->arc[k][j];
                }