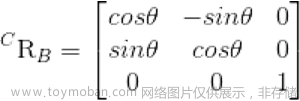目录
一、机器人选型
二、机器人DH参数和正运动学
(一)、DH参数
(二)、正运动学
三、工作空间绘制
四、构型分析
五、附录
一、机器人选型
UR协作机器人系列是优傲公司的代表产品,也是目前比较通用的产品级机械臂。选取UR系列的UR5协作机器人,产品参数如下:

二、机器人DH参数和正运动学
(一)、DH参数
机械臂的正运动学是把机械臂的关节变量作为自变量,描述机械臂末端执行器的位置和姿态与机械臂基座之间的函数关系。
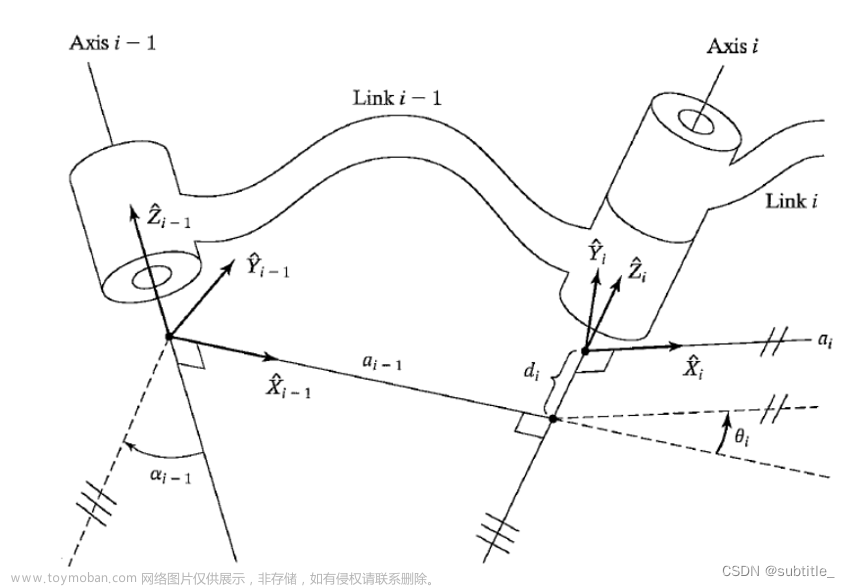
将各关节简化为圆柱体,将如下状态视为初始状态,用标准DH法建立坐标如下:

坐标系1,2,3,4,5,6是各个关节的坐标,其中坐标系2,3,4,5,6由于Zn-1和Zn 共面而导致坐标系偏离实际关节中心(坐标系应建立在Zn-1 和Zn 的交点处),坐标系7是机械臂末端点的位姿。
得到下列DH参数表:

其中,由机械臂参数可得:

保留theta变量,将常量代入DH参数表,即:

(二)、正运动学
下面根据DH表推导UR5机器人正运动学。
标准DH法坐标系n到n+1的变换矩阵如下:

观察DH参数表,可以知道α 均为0或±90°,故cosα 、sinα 均为0或±1,这里先将其带入其次变换矩阵,这一步是为了方便后续编程进行符号运算。

则有:

利用matlab在画布上画出机器人验证DH法推导过程是否正确,绘制出的机器人构型和模拟运动符合预期(完整视频可见附录):

三、工作空间绘制
将正运动学得到的齐次变换矩阵输入matlab代码文件中,利用matlab符号运算得出夹具末端位置坐标点的计算公式:

为了减少函数调用的时间,可以先将所有点的位置计算出来,这样只需调用一次绘图函数即可绘制所有的点。这样的做节省的是调用绘图函数的时间。即使先计算点的坐标,算法的时间复杂度仍然没有下降。
实际上,在Matlab或Pyhton等语言中,调用库函数或者自带的矩阵运算操作会比自己写for循环快得多,因为库函数和矩阵变换一般会有更底层语言的代码支持。
利用上述思想,我的做法是使用ndgrid函数建立网格坐标,省去for循环优化处理的速度。再使用plot3或scatter3函数进行工作空间绘制。ndgrid是一个网格坐标生成函数,和python的meshgrid异曲同工。对于传入的多个向量,函数返回由这些向量中的点所构成给的网格点的坐标。如调用如下语句:
[x1,x2]=ndgrid([1,2,3],[4,5,6])则函数会返回:

当我们把x1和x2中每个位置的数匹配起来看:
会得到:

我们将Ans展开即可得到:分别从数列1,2,3和数列4,5,6中各取一个数的所有可能情况。故我们可以将六个角度的范围传入ndgrid来得到所有角度的组合,来得到角度所有可能的组合。再利用对矩阵取cos、sin以及加减等操作,得到最终包含所有点的x,y,z坐标的向量。
使用此方式绘制得到的工作空间如下:

上述的优化始终改变不了算法的时间复杂度,一切的投机取巧终究还是班门弄斧,改变不了算法复杂本质。想要加快绘制的速度,除非换个算法,这里有一个更快而且能更好的拟合工作空间的算法:蒙特卡洛法。
当我们随机地取一定数量的θ ,当取的数量“足够多”时,就可以很好得描述工作空间的形状。显然这里的“足够多”可以远远小于十的九次方 。相比之前的方法,本方法得到的点云虽然稀疏,但很均匀。更能描述工作空间的形状。而且算法实现也很简单。当取1000个点时,效果如下:

查阅官方的数据手册:UR5机器人的工作空间是指机座关节周围一定空间内的球形区域除去机械臂上方的圆柱形区域。

观察上述图像,可以推断,如果∆θ 很小时,得出的工作空间确实是一个球。这里还有一个问题,除去的圆柱形区域在我们所绘制的空间中没有体现,这一点将在关节构型处分析。
上述算法的流程图如下:

蒙特卡洛法虽然又快又准,但形态上却看不出变化的过程。暴力枚举法虽然难以达到理想的结果,但每一次的蜕变都会带来形态上变化。好比生活并不只看结果,享受过程又何尝不是一种快乐。
四、构型分析
对于UR5机器人,先只考虑机器人的第六个关节:

由于最后一个关节的旋转,它的轨迹是一个点。
接着考虑第五、第六两个关节:

上一步中的点绕一个轴纯旋转,最后得到的是轨迹是一个圆形的轨迹线。
设如图所示P点的坐标为初始坐标,旋转的半径为r1,则轨迹为:

再考虑倒数第三个关节:

即一个圆形线绕着一根平行于该线所在平面的线旋转,主视图如上,最终的轨迹应该是一个带孔的圆柱:

其中:

最终得到轨迹如下:

考虑倒数第四个关节:

将带孔圆柱绕着一条平行于带孔圆柱轴线的直线进行旋转,这里有两种可能:

(1)

(2)
情况(1)关节在带孔圆柱内部,旋转的结果是一个不带孔的圆柱;
情况(2)关节在带孔圆柱外部,旋转的结果仍然是一个带孔的圆柱
对于UR5来说这里属于第二种情况:

有:

得到的仍然是带孔圆柱。
再考虑倒数第五个关节,此种情况同上种情况类似,但此时属于情况(1),故得到是一个完整的圆柱:

有:

再考虑最后一个关节,俯视图:


图中的矩形代表上一环节圆柱的侧视图,这种情况下的俯视图是一个矩形绕一个点进行旋转,最后得到的结果应该是一个带圆柱形通孔的球状区域,注意这里并不是一个标准的球形区域,因为俯视图和主视图的半径并不一样:
(1)对于俯视图:

其中,圆柱形通孔的半径为:

外圆形的半径为:

(2)对于主视图 :



代入参数计算可得:




观察上述式子可以看到:

由于主视图横竖近似相等,故可将主视图看成一个标准圆形。
由于俯视图内外半径差距极大,故可将俯视图看出一个标准的圆形。
我认为这也是使用Matlab绘制出来的工作空间看不出空心圆柱的原因。文章来源:https://www.toymoban.com/news/detail-775700.html
五、附录
UR5机器人运动模拟文章来源地址https://www.toymoban.com/news/detail-775700.html
到了这里,关于GDUT自动化创卓机器人学课程大作业:机械臂工作空间绘制的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!