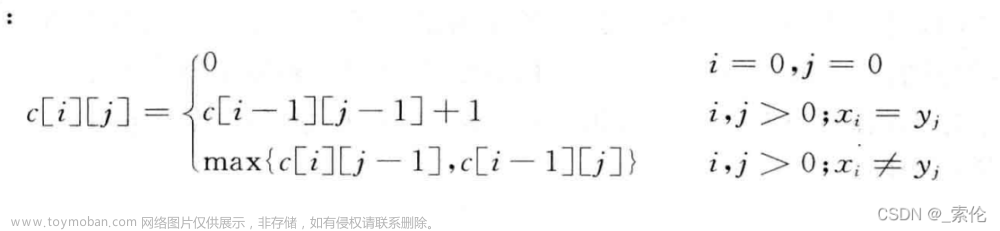点一点了解更多,动态规划,简单来说就是利用子结果来求下一次的结果,避免我们重复计算
目录
一、动态规划
二、简单动态规划——青蛙跳台阶
三、经典动态规划——最长公共子序列问题
3.1最短公共超序列
一、动态规划
动态规划,简单来说就是利用子结果来求下一次的结果,避免我们重复计算,子结果一般是用变量来保存,一般是用一维数组或者二维数组来保存。简单来说分三步:
- 第一步:定义数组元素的含义,我们要学会怎么去定义数组dp[],dp[i]代表什么意思?
- 第二步:找出数组元素之间的关系式,当我们要计算dp[n]时,是可以利用dp[n-1],dp[n-2]....dp[1],来推出dp[n],也就是可以利用子结果去推出新的元素值,重点就是找到数组元素之间的关系,例如dp[n] = dp[n-1]+dp[n-2],这个就是他们的关系
- 第三步:找出初始值,也就是最开始的值,例如dp[1],dp[2].....,有了初始值,根据关系式就可以推出dp[n],而 dp[n] 的含义是由你来定义的。
二、简单动态规划——青蛙跳台阶
问题:一只青蛙一次可以跳上一阶台阶,也可以跳上二阶。求该青蛙跳上一个n级的台阶总共有多少种跳法。
按照上面的三步,分别来求出dp数组的含义,初始值,dp[n]的关系式,dp[n] 一定会和 dp[n-1], dp[n-2]….存在某种关系的。
因为跳台阶可以选择跳一级和跳俩级,那么青蛙到达第 n 级的台阶有两种方式,一种是从第 n-1 级跳上来,一种是从第 n-2 级跳上来。
要求所有结果,所以dp[n] = dp[n-1] + dp[n-2]
初始条件:dp[1] = 1,dp[0] = 0。因为0个台阶就有一种跳法,1个台阶也是一种跳法
int dpCount( int n ){
if(n <= 1)
return n;
// 先创建一个数组来保存历史数据
int[] dp = new int[n+1];
// 给出初始值
dp[0] = 0;
dp[1] = 1;
// 通过关系式来计算出 dp[n]
for(int i = 2; i <= n; i++){
dp[i] = dp[i-1] + dp[i-2];
}
// 把最终结果返回
return dp[n];
}当 n = 2 时,dp[2] = dp[1] + dp[0] = 1。这显然是错误的,所以自己计算一下,计算量不大,所以dp[2] = 2,也就是说,在寻找初始值的时候,一定要注意不要找漏了,dp[2] 也算是一个初始值,不能通过公式计算得出。
三、经典动态规划——最长公共子序列问题
最长公共子序列问题是典型的二维动态规划问题。
问题:
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。1143. 最长公共子序列 - 力扣(LeetCode)
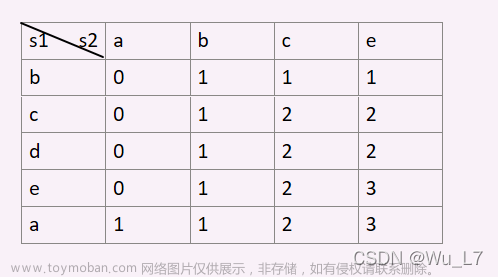
首先考虑dp[]怎么定义,因为是俩个字符串,所以定义一个二维数组 dp 用来存储最长公共子序列的长度,其中 dp[i][j] 表示字符串s1前i个字符和字符串s2前j个字符最长公共子序列的长度,考虑俩个下标,i与 j的值是否相等
分俩种情况:
当s1[i] == s2[j]:f[i][j] = f[i−1][j−1]+1- 当
s1[i] != s2[j]:f[i][j] = max(f[i−1][j],f[i][j−1])

class Solution {
public int longestCommonSubsequence(String text1, String text2) {
int m = text1.length(), n = text2.length();
int[][] dp = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
char c1 = text1.charAt(i - 1);
for (int j = 1; j <= n; j++) {
char c2 = text2.charAt(j - 1);
if (c1 == c2) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[m][n];
}
}
3.1最短公共超序列
给出两个字符串 str1 和 str2,返回同时以 str1 和 str2 作为子序列的最短字符串。如果答案不止一个,则可以返回满足条件的任意一个答案。
(如果从字符串 T 中删除一些字符(也可能不删除,并且选出的这些字符可以位于 T 中的 任意位置),可以得到字符串 S,那么 S 就是 T 的子序列)
1092. 最短公共超序列 - 力扣(LeetCode)

建立 DP 数组,dp[i][j] 表示当字符串 str1 的位置 i 和字符串 str2 的位置 j 时的最长公共子序列。分为俩种情况:文章来源:https://www.toymoban.com/news/detail-775751.html
- 当 str1[i] 和 str2[j] 字符相等时,我们只需要从上一个状态转移到当前状态即可,即计数加一:f[i][j] = f[i−1][j−1]+1
- 当不相等时,f[i][j] = max(f[i−1][j],f[i][j−1]),如果 f[i][j]=f[i−1][j],则将 str1[i] 加入到答案序列,然后i-1;如果 f[i][j]=f[i][j-1],则将 str2[j] 加入到答案序列,然后j-1。
- 重复上述操作,直到 i=0 或j=0,然后将剩余的字符串加入到答案序列即可。
class Solution {
public String shortestCommonSupersequence(String str1, String str2) {
int m = str1.length(), n = str2.length();
int[][] f = new int[m + 1][n + 1];
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
if (str1.charAt(i - 1) == str2.charAt(j - 1)) {
f[i][j] = f[i - 1][j - 1] + 1;
} else {
f[i][j] = Math.max(f[i - 1][j], f[i][j - 1]);
}
}
}
int i = m, j = n;
StringBuilder ans = new StringBuilder();
while (i > 0 || j > 0) {
if (i == 0) {
ans.append(str2.charAt(--j));
} else if (j == 0) {
ans.append(str1.charAt(--i));
} else {
if (f[i][j] == f[i - 1][j]) {
ans.append(str1.charAt(--i));
} else if (f[i][j] == f[i][j - 1]) {
ans.append(str2.charAt(--j));
} else {
ans.append(str1.charAt(--i));
--j;
}
}
}
return ans.reverse().toString();
}
} 文章来源地址https://www.toymoban.com/news/detail-775751.html
文章来源地址https://www.toymoban.com/news/detail-775751.html
到了这里,关于动态规划之经典中的经典——公共最长子序列的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!