一. 二维数组与矩阵打印
二. 回型矩阵
1.题目
2.思路分析
3.代码实现
三. 蛇形矩阵
1.题目
2.思路分析
3.代码实现
四. 上三角矩阵
1.题目
2.思路分析
3.代码实现
五. 矩阵转置
1.题目
2.思路分析
3.代码实现
六. 总结
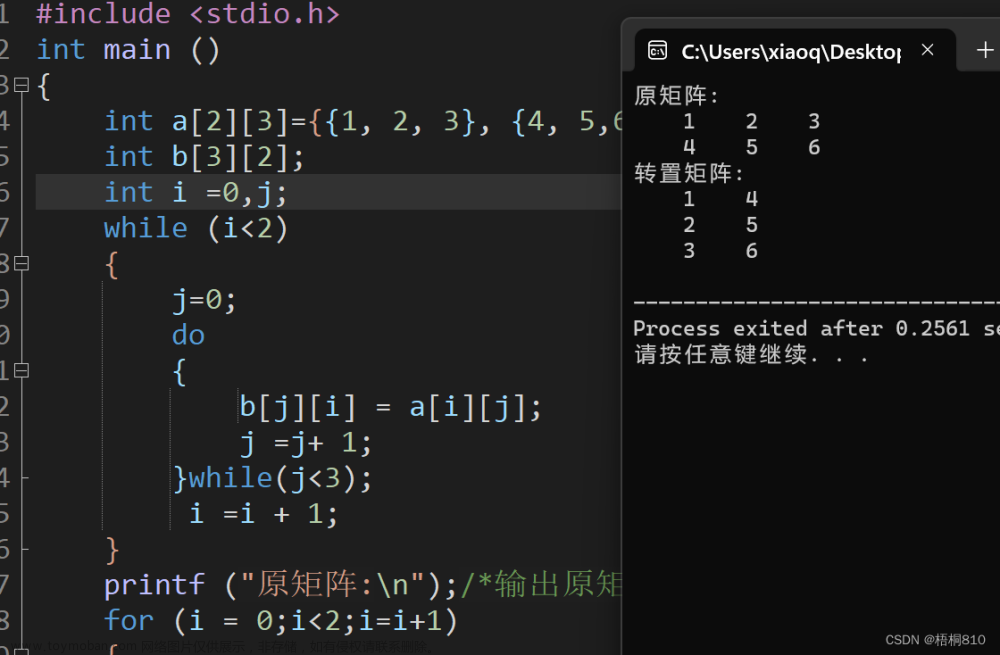
一. 二维数组与矩阵打印:
二维数组,作为一种存放一系列数的载体,不免和数学中用于存放数的数表——矩阵,有着密切的联系。矩阵本身就有些抽象,需要设计一个程序精准打印出来更是有难度,所以今天便来总结一些二维数组与矩阵打印的问题该如何解决。
(题目取自牛客网BC133-BC138)
二. 回型矩阵
1.题目:
BC133 回型矩阵
描述
给你一个整数n,按要求输出n∗n的回型矩阵
输入描述:
输入一行,包含一个整数n
1<=n<=19
输出描述:
输出n行,每行包含n个正整数.
示例1
输入:4
输出:1 2 3 4
12 13 14 5
11 16 15 6
10 9 8 7
2.思路分析:

分为内循环与外循环:外循环每循环一次就是打印一圈,逐次朝里,边界不断缩小;内循环分为4个,每个循环就是图中划分的(同色为一组)先从左向右、再从上向下、再从右向左、再从下向上打印;
外循环的注意点1——循环终止条件:start<over(找规律得出的,这种通常都是找规律得出的,最好奇数偶数的情况都试一下,再下结论);
外循环的注意点2——循环变量的改变:每循环一次:start++,over--(也是找规律得到的);
内循环的注意点:开始和结束,用start和over表示,要仔细考虑;
奇数的最后一个数,是start=over的情况,不被包含在循环里,所以要补在最后。
3.代码实现:
#include <stdio.h>
int main()
{
int n, i, j, step = 1,arr[20][20] = { 0 };
scanf("%d", &n);
int start = 0, over = n - 1;//对第一次循环的起始和终止条件,进行初始化;
//主体部分:原因详见上方的分析;
while (start < over)//外循环:每循环一次就打印一圈,逐次朝里,边界不断缩小;
{
//内循环分为4个,先从左向右、再从上向下、再从右向左、再从下向上打印;
for (j = start; j <= over; j++)
{
arr[start][j] = step;
step++;
}
for (i = start + 1; i <= over; i++)
{
arr[i][over] = step;
step++;
}
for (j = over - 1; j >= start; j--)
{
arr[over][j] = step;
step++;
}
for (i = over - 1; i > start; i--)
{
arr[i][start] = step;
step++;
}
start++;
over--;
}
//奇数补的那种start=over的情况:
if (n % 2)
{
arr[over][over] = n * n;
}
//把排好的矩阵打印出来:
for (i = 0; i < n; i++)
{
for (j = 0; j < n; j++)
{
printf("%d ", arr[i][j]);
}
printf("\n");
}
return 0;
}三. 蛇形矩阵
1.题目:
BC134 蛇形矩阵
描述
给你一个整数n,输出n∗n的蛇形矩阵。
输入描述:
输入一行,包含一个整数n
输出描述:
输出n行,每行包含n个正整数,通过空格分隔。
1<=n<=1000
示例1
输入:4
输出:1 2 6 7
3 5 8 13
4 9 12 14
10 11 15 16
2.思路分析:

首先,这个矩阵的排列,刚开始会觉得有些抽象,有点难以下手,所以需要从一些简单的例子中寻找总结出规律,所以画图找下标关系很重要!!!
规律1:连续的几个行列坐标和相同,且这个和不断增长;
规律2:和为奇数的都是行下标从0到和的值,而和为偶数的都是行下标从和的值到0;
规律3:下标和大于等于n时,下标标不再是从0开始,但可以确定的是行/列的上限是n-1,另一个通过和减来得出;
终止条件:arr[n-1][n-1];
3.代码实现:
#include <stdio.h>
int main()
{
int n, i, j, step = 2, sum = 1, arr[1000][1000] = { 0 };
scanf("%d", &n);
arr[0][0] = 1;
while (sum < n)
{
if (sum % 2)
{
for (i = 0; i <= sum; i++)
{
arr[i][sum-i] = step;
step++;
}
}
else
{
for (i = sum; i >= 0; i--)
{
arr[i][sum-i] = step;
step++;
}
}
sum++;
}
while (sum <= 2 * (n - 1))
{
if (sum % 2)
{
for (i = sum-n+1; i <= n-1; i++)
{
arr[i][sum-i] = step;
step++;
}
}
else
{
for (i = n - 1; i >= sum - n + 1; i--)
{
arr[i][sum-i] = step;
step++;
}
}
sum++;
}
for (i = 0; i < n; i++)
{
for (j = 0; j < n; j++)
{
printf("%d ", arr[i][j]);
}
printf("\n");
}
return 0;
}四. 上三角矩阵
1.题目:
BC136 KiKi判断上三角矩阵
描述
KiKi想知道一个n阶方矩是否为上三角矩阵,请帮他编程判定。上三角矩阵即主对角线以下的元素都为0的矩阵,主对角线为从矩阵的左上角至右下角的连线。
输入描述:
第一行包含一个整数n,表示一个方阵包含n行n列,用空格分隔。 (2≤n≤10)
从2到n+1行,每行输入n个整数(范围-231~231-1),用空格分隔,共输入n*n个数。
输出描述:
一行,如果输入方阵是上三角矩阵输出"YES"并换行,否则输出"NO"并换行。
示例1
输入:3
1 2 3
0 4 5
0 0 6
输出:YES
示例2
输入:4
1 2 3 4
5 6 7 8
9 0 11 12
13 0 0 16
输出:NO
2.思路分析:

这题规律比较容易看出来,主要思路是遍历下三角区域(即该为零的区域),这个区域就是j<i的情况。
3.代码实现:
#include <stdio.h>
int main()
{
int n,i,j,flag=1,arr[10][10]={0};
scanf("%d",&n);
for(i=0;i<n;i++)
{
for(j=0;j<n;j++)
{
scanf("%d",&arr[i][j]);
}
}
for(i=1;i<n;i++)
{
for(j=0;j<i;j++)
{
if(arr[i][j]!=0)
{
flag=0;
break;
}
}
}
if(1==flag)
{
printf("YES\n");
}
else
{
printf("NO\n");
}
return 0;
}五. 矩阵转置
1.题目:
BC138 矩阵转置
描述
KiKi有一个矩阵,他想知道转置后的矩阵(将矩阵的行列互换得到的新矩阵称为转置矩阵),请编程帮他解答。
输入描述:
第一行包含两个整数n和m,表示一个矩阵包含n行m列,用空格分隔。 (1≤n≤10,1≤m≤10)
从2到n+1行,每行输入m个整数(范围-231~231-1),用空格分隔,共输入n*m个数,表示第一个矩阵中的元素。
输出描述:
输出m行n列,为矩阵转置后的结果。每个数后面有一个空格。
示例1
输入:2 3
1 2 3
4 5 6
输出:1 4
2 5
3 6
2.思路分析:

这题也比较简单,规律就是i,j互换。
3.代码实现:
#include <stdio.h>
int main()
{
int n,m,i,j,matrix_T[10][10]={0};
scanf("%d %d",&n,&m);
for(i=0;i<n;i++)
{
for(j=0;j<m;j++)
{
scanf("%d",&matrix_T[j][i]);
}
}
for(i=0;i<m;i++)
{
for(j=0;j<n;j++)
{
printf("%d ",matrix_T[i][j]);
}
printf("\n");
}
return 0;
}六. 总结:
用二维数组打印矩阵的问题
①难点:抽象,难以入手;文章来源:https://www.toymoban.com/news/detail-775798.html
②解决方法:画简单情形的图(具象化),分奇数偶数两种情形,从中寻找下标间的规律,再利用循环来构建程序进行打印;所以从简单情形中,寻找总结规律是特别重要的。文章来源地址https://www.toymoban.com/news/detail-775798.html
到了这里,关于回型矩阵|蛇形矩阵|上三角矩阵|矩阵转置|二维数组打印问题的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!