FPGA实现PID控制器——基于Quartus prime 18.0

目录

 1. PID控制器和离散化PID控制器

1.1 PID控制器

1.1.1 P控制器

1.1.2 稳态误差和I控制器

1.1.3 超调和D控制器

1.2 离散式PID控制器——位置式PID控制器

2.PID控制系统Simulink仿真

3.Verilog代码编写和Modelsim仿真

3.1 误差计算模块和PID算法模块编写

3.1.1 误差计算模块

3.1.2 PID算法模块

3.2 主模块及Testbench模块编写

3.2.1 主模块编写

3.2.2 Testbench模块编写

3.3 仿真结果

 1. PID控制器和离散化PID控制器

1.1 PID控制器

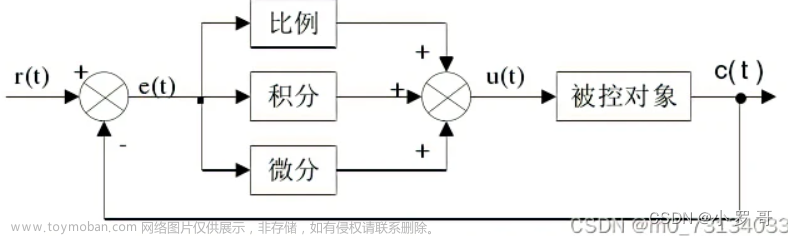
PID控制器中的P, I, D分别代表比例、积分、微分，它是一种用于控制工业应用中压力、流量、温度和速度等不同过程变量的设备。在该控制器中，控制回路反馈装置用于调节所有过程变量。

像PID控制器这样的闭环系统包括反馈控制系统。该系统使用固定点评估反馈变量以生成误差信号。在此基础上，它会改变系统输出。这个过程将一直持续到误差达到零，否则反馈变量的值就等于一个固定点。

1.1.1 P控制器

P控制器通过比例运算来调节系统输出和目标值之间的误差。例如系统输出为5，目标值为10，当设定P控制器的比例系数为Kp=0.8时，则有如下计算过程：

通过误差和比例系数之间的直接乘法运算，P控制器实现了对误差的纠正。

由以上的例子可以看出，当Kp的值越大时，系统达到稳态（即输出值等于目标值）的速度也就越快，但是当Kp的值过大时，系统的输出误差绝对值并不一定减小，例如将上例的Kp改为2，则误差e(t)由P控制前的5变为了控制后的-5，实际上，当Kp的值过大时，误差的绝对值有可能越来越大，导致系统输出进入发散状态。

1.1.2 稳态误差和I控制器

在实际的系统控制中，系统往往存在阻尼或其他形式的消耗。例如一个力学系统中可能会有摩擦，热学系统可能存在热能耗散等等。这将会导致我们输出的比例控制并不能完全地转化为系统输出。例如一个热力学系统每秒向外耗散0.5℃的热量，当误差为1℃且Kp=0.5时，输出值与目标值之间将永远存在1℃的误差。这部分误差即为稳态误差。

在这种情况下便需要积分控制来消除这一部分误差。通过引入对误差的积分值，我们便可以在一次积分控制中对前一段时刻产生的误差累积量进行控制，即

通过这样的方式，当系统存在稳态误差时，积分项的误差累积值将会越来越大，从而实现了稳态误差的消除。

1.1.3 超调和D控制器

在控制系统中，我们往往很难一次就将输出值控制到与目标值相等，为使系统更快地达到稳态，往往选用较大的比例系数Kp，从而会导致系统的输出会先高于目标值，然后又低于目标值，这样在反复震荡的过程中振幅逐渐减小，最终达到稳态值。在这个过程中系统的输出信号超过目标值的现象就称为超调现象，超出的值就称为超调量。在此过程中超调量的最大值称为最大超调量。一般来说，在系统输出不发散的前提下，比例系数越大，超调量也就越大，系统达到稳态的速度也越快。但是超调量过大时，系统的稳定性也会变差，在许多实际场景中，这是我们不愿看到的。因此我们引入微分控制，来对系统的超调和震荡进行控制。

我们知道，微分表示了一个函数图像的斜率，即当前时刻的变化率。因此，对当前时刻的误差e(t)进行微分运算，便可得到当前时刻误差的变化率，也就可以预测出下一时刻误差的变化趋势。因此通过这一手段，我们便可以在当前时刻提前对控制信号做出调整，从而在误差减小或是增大时加快或减小控制信号的输出。我们在向杯子里倒水时，随着水越来越满（误差越来越小），逐渐减慢倒水的速度，就可以理解为是一个微分控制的过程。微分控制的公式如下：

将比例P，积分I，微分D三部分的公式合在一起，便得到了PID控制算法的计算公式：

在工程中，PID控制器的系数KP、KI、和KD需要结合实际给出，即PID参数整定。这里不再给出整定的具体方法，大家可以自行搜索查阅。

1.2 离散式PID控制器——位置式PID控制器

无论计算机还是FPGA芯片，采取的控制方式都是采样控制，只能根据采样时刻的偏差来计算控制量，因此计算机控制系统中，必须对公式进行离散化，具体就是用求和代替积分，用向后差分来代替微分，使模拟PID离散化为数字形式的差分方程。

离散式的PID控制算法主要有位置式PID和增量式PID两种，本文使用的是位置式PID控制。由上文给出的PID控制算法：

对于离散信号而言，取某一采样点k，此时的误差e(t)为e(k)。则比例项的误差值就是e(k)，而积分项可以用之前时段误差值的累加得到，即

同理，微分项的误差变化率也可以用当前时刻误差减去上一时刻误差得到，即

其中，T为采样周期。

在PID控制公式中，可将KI，KD写作另一种形式，如下：

式中引入了积分时间常数TI和微分时间常数TD，从而使得KI和KD得以用KP表示出来。由此可以得出离散PID控制的公式：

由此得出的即为离散PID控制的位置式算法。

2.PID控制系统Simulink仿真

利用Simulink对控制系统进行仿真，主要目的是选取合适的PID参数，并获取输入输出数据，便于使用Modelsim进行Verilog代码的仿真，并将Simulink的仿真结果与Modelsim仿真结果对比，验证仿真的正确性。搭建的控制系统框图如下：

图中目标信号输入为阶跃信号，初值为0，终值为1，阶跃时间为1s。PID参数KP=50，KI=100，KD=3。将target和sig_in的值输出到工作区，作为Modelsim仿真时的输入量。将仿真运行5s，结果如图所示：

上图中，上方曲线为误差信号，中间曲线为系统输出，也是下一时刻反馈信号输入，即Modelsim仿真中控制器的输入sig_in，下方曲线为控制器输出，即Modelsim仿真中的输出ctrl_out。

输出到Matlab工作区的值target和sig_in需要经过处理才能输入到Modelsim，Matlab处理代码如下：

% 将数据左移7位并取整，保留前七位并换算为整数方便计算
sig_in = round(sig_in * 1000000);
target = round(target * 1000000);

% 将十进制数转化为十六进制数
sig_in = dec2hex(sig_in);
target = dec2hex(target);

% 将数据保存为txt格式
% sig_in
in = fopen('sig_in.txt','wt');
fprintf(in,'%g\n',sig_in);
fclose(in);
% target
tgt = fopen('target.txt','wt');
fprintf(tgt,'%g\n',target);
fclose(tgt);

处理后即得到十六进制的输入数据。注意Matlab的十六进制数会保存为字符串格式，在输入到Modelsim仿真中时需要再次处理（实际上把引号删除即可）。

3.Verilog代码编写和Modelsim仿真

PID控制器的Verilog代码分为三个部分：误差计算模块、PID算法模块和主模块。

3.1 误差计算模块和PID算法模块编写

3.1.1 误差计算模块

误差计算模块的主要功能为计算比例项、积分项和微分项的误差值，并对积分项的误差累加值进行限幅，代码如下：

module error (
        input  wire                         clk     ,   // 时钟信号
        input  wire                         rstn    ,   // 复位信号
        input  wire     signed     [31:0]   sig_in  ,   // 反馈信号输入
        input  wire     signed     [31:0]   target  ,   // 目标信号

        output reg      signed     [31:0]   error   ,   // 当前状态误差信号
        output reg      signed     [31:0]   error1  ,   // 上一状态误差信号
        output reg      signed     [31:0]   sum_e       // 误差信号累加值 用于积分环节
    );

    parameter [31:0] itg_max = 32'd100000000     ;       // 积分限幅，最大累加值为100
    parameter [31:0] itg_min = -32'd100000000    ;       // 积分限幅，最小累加值为-100
    always @(posedge clk or negedge rstn) begin
        if(!rstn) begin             // 复位
            error  <= 32'd0 ;
            error1 <= 32'd0 ;
            sum_e  <= 32'd0 ;
        end
        else begin
            error  <= target - sig_in   ;       // 误差信号e = 目标信号t - 反馈信号s
            error1 <= error             ;       // 将误差信号打一拍 得到上一时刻的误差值
            // 由于二进制数使用补码表示正负，因此限幅的条件与简单的十进制数表示方法存在差异
            if ((sum_e > itg_max) && (sum_e < 32'h7FFF_FFFF)) begin
                sum_e <= itg_max;
            end
            else if ((sum_e < itg_min) && (sum_e > 32'h8000_0000)) begin
                sum_e <= itg_min;
            end
            else
                sum_e  <= sum_e + error     ;       // 积分误差累加                     
        end
    end

endmodule

由于Verilog程序中需要给定输入输出的位宽，因此限幅功能也可以不加

3.1.2 PID算法模块

PID算法模块对误差模块输出的误差进行处理，输出PID控制器输出，代码如下：

module pid_ctrl (
        input  wire                clk     ,    // 时钟
        input  wire                rstn    ,    // 复位
        input  wire signed [31:0]  error   ,    // 误差
        input  wire signed [31:0]  error1  ,    // 上一时刻误差
        input  wire signed [31:0]  sum_e   ,    // 误差累加值

        input  wire signed [7:0]   kp      ,    // 比例系数
        input  wire signed [7:0]   ki      ,    // 积分系数
        input  wire signed [7:0]   kd      ,    // 微分系数

        output reg  signed [63:0]  ctrl_out     // 控制器输出
    );

    always @(posedge clk or negedge rstn) begin
        if(! rstn) begin
            ctrl_out <= 64'd0;
        end
        else begin
            ctrl_out <= (kp*error) + (ki*sum_e) + (kd*(error - error1));    // PID计算
        end
    end

endmodule

3.2 主模块及Testbench模块编写

3.2.1 主模块编写

主模块只需将两个模块依次例化即可，代码如下：

module pid_controller (
        input  wire                  clk      ,      // 时钟50MHz
        input  wire                  rstn     ,      // 复位信号
        input  wire signed [31:0]    sig_in   ,      // 反馈信号输入
        input  wire signed [31:0]    target   ,      // 目标信号

        input  wire signed [7:0]     kp       ,      // 比例环节系数
        input  wire signed [7:0]     ki       ,      // 积分环节系数
        input  wire signed [7:0]     kd       ,      // 微分环节系数

        output wire signed [63:0]    ctrl_out        // 控制信号输出
    );

    wire     [31:0]  error   ;
    wire     [31:0]  error1  ;
    wire     [31:0]  sum_e   ;
    error error_inst (
              .clk            (clk)       ,
              .rstn           (rstn)      ,
              .sig_in         (sig_in)    ,
              .target         (target)    ,
              .error          (error)     ,
              .error1         (error1)    ,
              .sum_e          (sum_e)
          );

    pid_ctrl pid_ctrl_inst (
                 .clk            (clk)     ,
                 .rstn           (rstn)    ,
                 .error          (error)   ,
                 .error1         (error1)  ,
                 .sum_e          (sum_e)   ,
                 .kp             (kp)      ,
                 .ki             (ki)      ,
                 .kd             (kd)      ,
                 .ctrl_out       (ctrl_out)
             );

endmodule

3.2.2 Testbench模块编写

代码如下：

`timescale 1ps/1ps
module pid_controller_tb;

    //Ports
    reg                         clk     ;
    reg                         rstn    ;
    reg   signed  [31:0]        sig_in  ;
    reg   signed  [31:0]        target  ;
    reg   signed  [7:0]         kp      ;
    reg   signed  [7:0]         ki      ;
    reg   signed  [7:0]         kd      ;
    wire  signed  [63:0]        ctrl_out;

    integer i;
    reg [31:0]  txt_in       [0:500-1]  ;
    reg [31:0]  txt_target   [0:500-1]  ;
    reg [7:0]   count                   ;
    reg [15:0]  file                    ;
    initial begin
        $readmemh("sig_in.txt", txt_in);      // 读取输入信号sig_in
        $readmemh("target.txt", txt_target);  // 读取输入信号target
        file = $fopen("ctrl_out.txt","w");    // 建立新文件用于保存输出ctrl_out
    end
    initial begin   
        // 给定PID系数，数值与上面不同，原因见下 3.3
        kp      =   8'd50  ;
        ki      =   8'd1   ;
        kd      =   8'd300 ;
        //开启时钟及复位
        clk     =   1'b0    ;
        rstn    =   1'b1    ;
        # 5;
        rstn    =   1'b0    ;
        # 5;
        rstn    =   1'b1    ;
        // 依次读取输入数据
        for (i = 0;i <= 500; i = i + 1) begin
            sig_in = txt_in[i]      ;
            target = txt_target[i]  ;
            #10;
        end
    end

    pid_controller pid_controller_inst (
                       .clk         (clk)       ,
                       .rstn        (rstn)      ,
                       .sig_in      (sig_in)    ,
                       .target      (target)    ,
                       .kp          (kp)        ,
                       .ki          (ki)        ,
                       .kd          (kd)        ,
                       .ctrl_out    (ctrl_out)
                   );

    always #5  clk = ~clk ;
    // 将ctrl_out保存到txt文件
    always @(posedge clk) begin
        if (count < 8'd500) begin
            $fwrite(file,"%d\n", ctrl_out);
            count <= count + 1;
        end
        else begin
            count <= 8'd0;
            $fclose(file);   // 关闭文件读写
        end
    end

endmodule

3.3 仿真结果

利用Modelsim进行仿真，结果如下图：

由上图可看出，Modelsim输出的波形与图2中Matlab中的仿真波形基本一致，将输出的ctrl_out.txt进行处理后放入Matlab工作区（保存为矩阵D），导入到Simulink中代替PID控制器的输出，框图如下：

仿真5s，在scope“输出比较”模块中观察输出信号，如下图：

由上图不难看出，两个输出的信号波形基本相同。

在Testbench文件中，使用的PID控制系数与仿真时的系数不同。如果仍使用KP=50，KI=100，KD=3的系数结果如下图：

由离散PID算法的公式：

可以看出相比于连续的PID控制算法，式中多了采样周期T，因此离散PID的参数与连续PID的参数相比应该多一个采样周期T，即：

经处理后KI=1，KD=300，修正后的PID参数即可得出正确的仿真值。文章来源地址https://www.toymoban.com/news/detail-775837.html

到了这里，关于FPGA实现PID控制器——基于Quartus prime 18.0的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！