最小生成树——Kruskal算法详解-Toy模板网

这篇具有很好参考价值的文章主要介绍了最小生成树——Kruskal算法详解。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

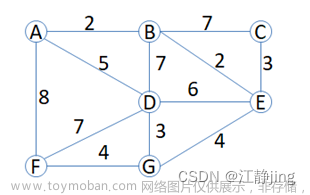
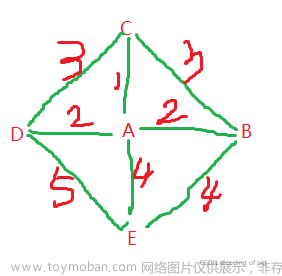
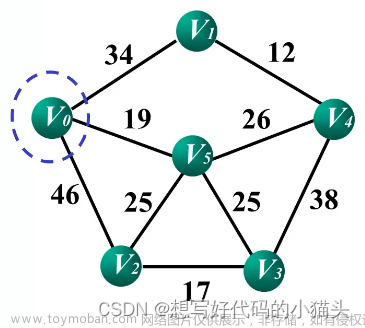
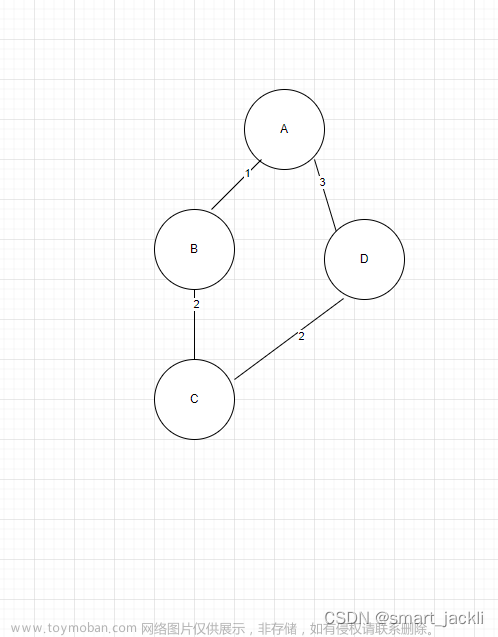
1.Kruskal算法解决问题：最小生成树
2.Kruskal所需要的前提知识：边集数组（引用）和结构体
3.Kruskal算法主要思想：

Kruskal算法将 n 个点看成 n 个独立的连通分支。

首先按边权大小排序。

然后只要在 m 条边里按下表从小到大遍历选出合适的 n - 1 条（前提条件：选出的边不能成自环，否则将无法连通），就是一个最小生成树。

Q：怎么确定选出的是 合适 的？
A：聪明的 Joseph Kruskal 早就想到了这个问题，他用一个 int nodeset[] 数组来表示当前节点属于哪个“连通块”，如果要连接 A 和 B，那就需要所有属于 nodeset[A] 集合的点的 nodeset 值都变成 nodeset[B]，简单来说，就是合并 A 与 B

4.Kruskal算法实现步骤：

1.初始化，将所有边都按权值从小到大排序，将每个节点的 nodeset 值都初始化为自己的编号，即 nodeset[i] = i;注意！！！要用边集数组！！！
2.按排序后的顺序选择最小的边(u, v);
3(1).如果 nodeset[u] == nodeset[v], 说明加入这条边了之后会有环，所以要舍;
3(2).如果 nodeset[u] != nodeset[v], 说明加入了这条边之后没有环，所以合并 u所在的集合 与 v所在的集合;
4.重复执行 2 和 3 直到已经加入了 n - 1 条边.
算法结束

5.Kruskal算法实现代码：

#include <iostream>
#include <algorithm> //sort头文件
using namespace std;
struct node { //边集数组
	int u, v, w;
}e[1000005];
int nodeset[1000005], n, m;
bool cmp(node a, node b) { //sort判断条件
	return a.w < b.w;
}
bool merge(int u, int v) {
	int uu = nodeset[u], vv = nodeset[v];
	if (uu == vv) {
		return false;
	}
	//uu != vv 的话就合并 uu 和 vv
	for (int i = 1; i <= n; i++) {
		if (nodeset[i] == uu) {
			nodeset[i] = vv;
		}
	}
	return true;
}
void kruskal(int n) {
	int ans = 0, cnt = 0;
	for (int i = 1; i <= m; i++) { //按顺序遍历 m 边集数组
		int from = e[i].u, to = e[i].v, value = e[i].w;
		if (merge(from, to)) { //需要合并，即3(2)
			ans += value; //答案更新
			cnt++;
			if (cnt == n - 1) { //判断时候已经选取了 n - 1 个数
				break;
			}
		}
	}
	cout << ans;
}
int main() {
	int t;
	cin >> t;
	while (t--) {
		cin >> n >> m;
		//初始化
		for (int i = 1; i <= m; i++) {
			int u, v, w;
			cin >> u >> v >> w;
			e[i].u = u;
			e[i].v = v;
			e[i].w = w;
		}
		for (int i = 1; i <= n; i++) { //初始化 nodeset[]
			nodeset[i] = i;
		}
		sort(e + 1, e + m + 1, cmp); //边集数组排序
		kruskal(n);
	}
	return 0;
}