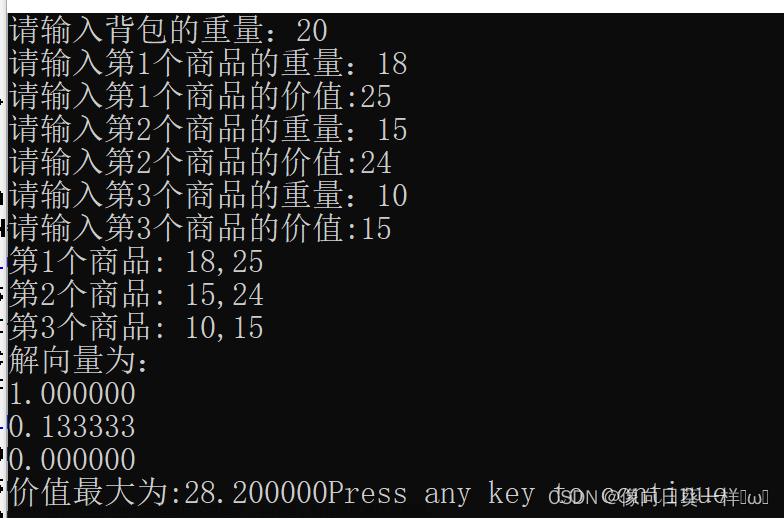
【程序设计竞赛算法】背包问题——贪心法
贪心算法是一种基于贪心策略的算法,它在每一步选择中都采取当前状态下的最优选择,以期望最终达到全局最优解。
背包问题是一个经典的组合优化问题,可以分为 0-1 背包问题和分数背包问题。其中,0-1 背包问题要求物品只能选择一次,而分数背包问题允许物品被选择多次。
贪心算法解决背包问题的原理如下:
1、对于 0-1 背包问题,贪心算法的思路是优先选择单位价值最高的物品放入背包中。即计算每个物品的单位价值(价值与重量的比值),然后按照单位价值从高到低进行排序。接着,从单位价值最高的物品开始,依次尝试将物品放入背包中,如果放入会超过背包容量,则跳过该物品;否则,将物品放入背包,并更新背包容量和总价值。重复这个过程,直到背包容量为 0 或所有物品都被考虑完毕。
2、对于分数背包问题,贪心算法的思路是优先选择单位价值最高的物品放入背包中,直到背包容量为 0 或所有物品都被考虑完毕。与 0-1 背包问题不同的是,分数背包问题允许物品被选择多次,因此可以按照单位价值从高到低进行排序后,依次选择整个物品或者部分物品放入背包,直到背包容量为 0。
下面是使用 C 语言给出一个贪心算法解决 0-1 背包问题的具体例子:
#include <stdio.h>
#include <stdlib.h>
// 物品结构体
typedef struct {
int weight; // 重量
int value; // 价值
} Item;
// 比较函数,用于按照单位价值从高到低排序
int compare(const void* a, const void* b) {
Item* item1 = (Item*)a;
Item* item2 = (Item*)b;
double ratio1 = (double)item1->value / item1->weight;
double ratio2 = (double)item2->value / item2->weight;
if (ratio1 < ratio2) {
return 1; // 比例大的在前
} else if (ratio1 > ratio2) {
return -1; // 比例小的在后
} else {
return 0;
}
}
// 贪心算法解决 0-1 背包问题
double knapsack(Item items[], int n, int capacity) {
qsort(items, n, sizeof(Item), compare); // 按照单位价值从高到低排序
double totalValue = 0.0; // 总价值
int currentWeight = 0; // 当前背包重量
for (int i = 0; i < n; i++) {
if (currentWeight + items[i].weight <= capacity) {
// 如果当前物品可以完整放入背包
currentWeight += items[i].weight;
totalValue += items[i].value;
} else {
// 如果当前物品只能放入部分
int remainingCapacity = capacity - currentWeight;
double fraction = (double)remainingCapacity / items[i].weight;
currentWeight += remainingCapacity;
totalValue += items[i].value * fraction;
break;
}
}
return totalValue;
}
int main() {
Item items[] = {
{10, 60},
{20, 100},
{30, 120}
};
int n = sizeof(items) / sizeof(items[0]);
int capacity = 50;
double maxValue = knapsack(items, n, capacity);
printf("背包中物品的最大总价值:%lf\n", maxValue);
return 0;
}
在上述代码中,我们首先定义了一个物品结构体 Item,包含物品的重量和价值。然后,我们定义了一个比较函数 compare,用于按照单位价值从高到低排序物品。
在 knapsack 函数中,我们首先调用 qsort 函数对物品数组 items[] 按照单位价值从高到低进行排序。接着,我们使用贪心策略,从单位价值最高的物品开始,尝试将物品放入背包中。如果物品可以完整放入背包,则将物品的重量加入当前背包重量,并将物品的价值加入总价值。如果物品只能放入部分,则计算出可以放入的部分重量,更新当前背包重量和总价值,并终止循环。
在 main 函数中,我们给定了一组物品的重量和价值,并设置背包容量为 50。通过调用 knapsack 函数,得到背包中物品的最大总价值,并输出结果。文章来源:https://www.toymoban.com/news/detail-776149.html
需要注意的是,贪心算法解决背包问题的结果不一定是最优解。在一般情况下,贪心算法无法保证得到全局最优解,因为它只考虑了局部最优情况。对于一些特殊情况的背包问题,贪心算法可能得到最优解,但对于一般的背包问题,通常需要使用动态规划等其他方法来获得最优解。文章来源地址https://www.toymoban.com/news/detail-776149.html
到了这里,关于【程序设计竞赛算法】背包问题——贪心法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!