动态规划,Dynamic Programing(简称DP),个人认为是一种算法思想,用来解决多阶段多层次的选择问题,把一个复杂的问题分解成每个小块的子问题然后一个个解决来找到最优解。
DP适用重叠子问题和最优子结构的性质的问题。
DP问题范围分为线性与非线性。线性DP可以顺推可以逆推,在理解过程我们可以尝试画出二维图进行理解;非线性DP类似树形图,可以从根到叶,也可以从叶到根。
在学习DP的过程我们或多或少的会遇到背包问题,咱们这里就谈谈01背包的想法与思路吧。作者是大一新生,发表文章表达自己对于背包问题的看法,希望高手可以指出不足,感谢!话不多说进入正题......
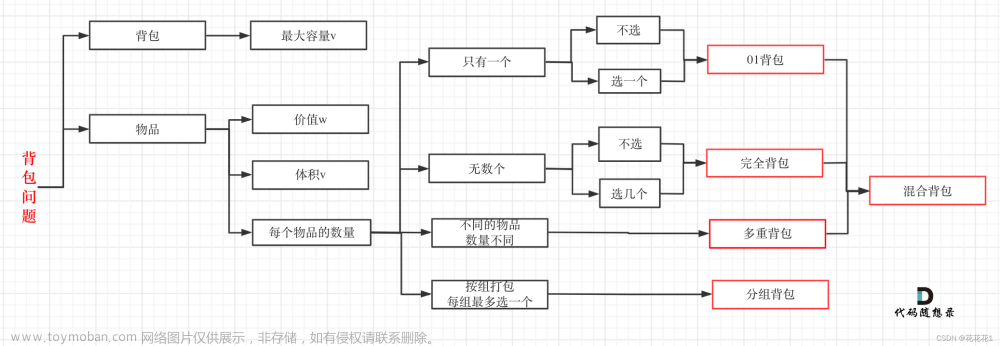
01背包是最经典的DP问题,为什么要学好01背包呢?是因为咱们很多题目是基于01背包的基础进行做题的,前面也提到了DP是一种算法思想,不要过于拘束。背包问题大概就是给你一个容量为V的背包以及多个物品,每个物品对应一个体积和其价值,这种题目咱们可以分成五个模块:
1.理解题干含义定义dp[i]的含义
2.分析题干关键部分找到状态转移方程
3.dp数组的初始化如何设计
4.如何正确的遍历dp数组
5.打印dp数组
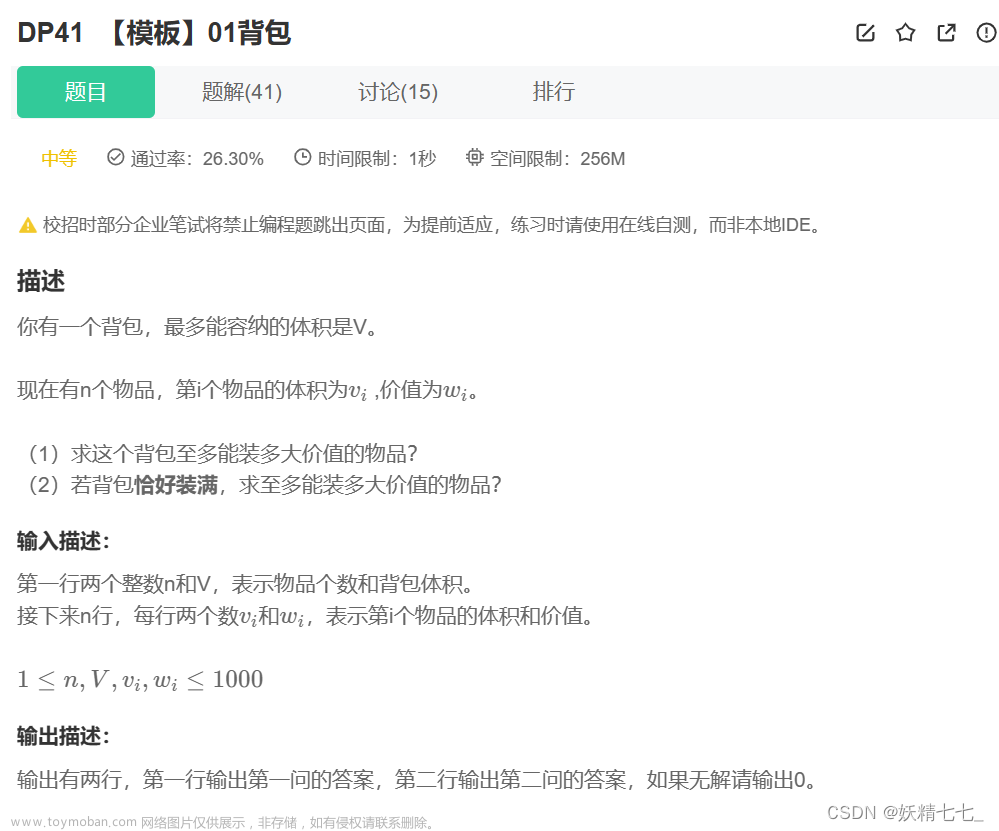
上面的五个模块是分析DP问题的步骤,下面我们通过题干来理解01背包的求法......
咱们按照五个模块分析题干:
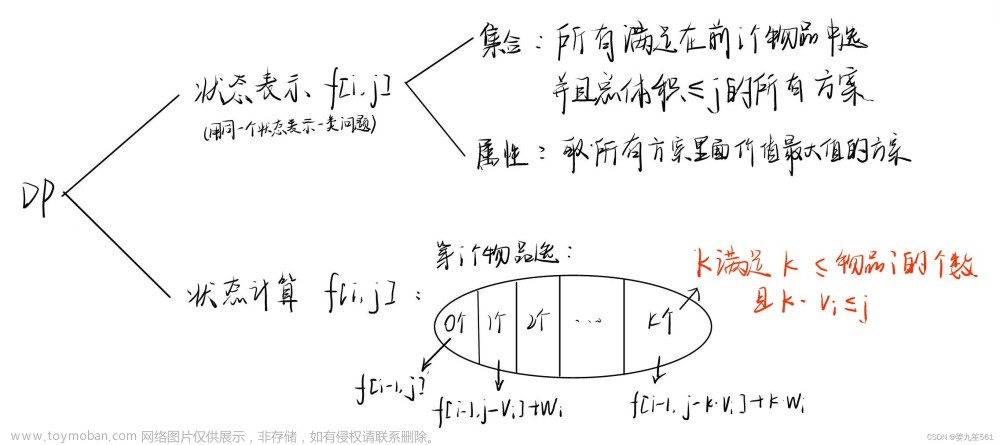
1.咱们分析如何定义dp数组的含义,在这里需要咱们细心阅读题干,题干表明背包容量是固定的,如果超过背包容量是不就代表无法拿这个物品,所以背包容量是其限制条件,如果咱们假设i为枚举到第i个物品,dp[i]代表当前的最大金额,在这里咱们要想给其加入限制条件,是不是可以开辟一个二维数组,因为二维数组内两个参数可以代表两个含义,所以设置dp[][],其中举个例子dp[i][j - w[i]]中i代表枚举到第几个物品,j - w[i]代表因为背包加入第i个物品导致背包空间剩下j - w[i]。
2.我们创建dp数组含义,接下来就该分析状态转移方程了。
最开始的情况是max(dp[1][i],dp[1][j - w[1]] + v[1]),因为我最开始拿第一个物品,他的选择情况只能是要么选择要么不选择,dp[1][j]代表不选而dp[1][j - w[1]]代表选择。注意一下这里是要最大金额,所以咱们要比较我是拿1才能使金额保持最大还是不拿1才能使金额最大,然后继续筛选,可以写出dp[i][j] = max(dp[i - 1][j],dp[i - 1][j - w[i]] + v[i]),这个就是状态转移方程。dp[i - 1][j]代表不选而dp[i - 1][j - w[i]]代表选择物品,其实个人认为核心思想就是去向问题,也就是将每个情况分别罗列出来来构成状态转移方程,这道题就是将你选和不选两种情况通过编程语言说明,然后要选出最大值,所以要在去向前加入max来保证选出的永远是最大金额。
这是个递推过程,你要明白如果你要是认为我怎么这样拿就可以拿到最大值了,那你肯定是跟我一样忘记了dp数组的含义,我们最开始dp数组设定的含义是要的是最大金额,也就是说在做DP,你要时刻记住不要忘记设置的dp数组本身的含义。个人理解这个想不明白就自己动手画出二维图,我的老师告诉我,你想不明白就自己把整个流程自己画一遍hhh,然后我花了一个多小时才搞明白(哭)。
如果要是还是想不明白,请看我主页内对于二维背包图的解释吧,这里先不介绍了hhh....
3.初始化.对于初始化如何做呢?我个人认为就是单纯的找边界,为了不让数组越界导致程序乱码,我们可以通过自己设置的dp数组的定义结合题意来理解。在本题我们可以发现dp[0] 代表的含义是选到第0个物品其最大金额,那显而易见dp[0] = 0。这道题初始化很简单,但是初始化切记一点,这道题是要最大金额,那我为什么不能初始化为2,3,4....以及1e9呢?(思考),因为你要是取1e9为初始值,你觉得后面再跟dp[0]比较还能有比他大的数了吗?哈哈哈哈,所以我们对于最大值问题可以设置<= 0 的数(思考)。
4.遍历数组。咱们这里很多人包括我也不理解为啥很多博主讲这些遍历顺序为啥都不一样啊(烦),这里推荐都能看到这里的朋友告诉你,这个东西靠听网课只能学到大概,但是细节需要自己理解,只有自己真正明白二维背包图怎么画才会真正初步会01背包的入门,我指的是含义,在二维做法其实大部分可以不需要考虑遍历顺序问题,不妨画一下图吧(如果你偷懒,来我主页看吧hhh),画完图你就明白他递推过程很有趣,跟dfs其实是不同的,但也不是完全不同。但是后期你要是学压维的时候你就要重点看遍历顺序问题了,我就不介绍了(没精力了抱歉)。
5.打印数组(看代码吧码不动了(哭))
#include <stdio.h>
const int N = 1000;
int w[N];//价值
int v[N];//重量
int f[N][N];//i表示遍历到第几个 j表示剩余容量
int max(int a,int b)
{
int res = a > b ? a : b;
return res;
}
int main()
{
int n,m;//n表示几个物品 m表示背包大小
scanf("%d %d",&n,&m);
for(int i = 1;i <= m;i++)
{
scanf("%d %d",&v[i],&w[i]);
}
for(int i = 1;i <= n;i++)//遍历物品,可以调换方向的
{
for(int j = 0;j <= m;j++)//背包容量,可以调换方向的
{
if(j < v[i])//筛掉背包空间不够的操作
{
f[i][j] = f[i - 1][j];
}
else
{
f[i][j] = max(f[i - 1][j],f[i - 1][j - v[i]] + w[i]);
}
}
}
printf("%d",f[n][m]);
return 0;
}看到这里喜欢各位能够理解他的含义,然后看完希望你做一些有关01背包的改动题,然后后期我会根据自己学习的方向写一下滚动数组(压维)。好了好了,感谢观看,希望点点关注,同时也希望大佬可以为我指点一下,个人是大一新生,对于算法路线些许迷茫,今天就到这里感谢观看(爱心)。文章来源:https://www.toymoban.com/news/detail-776166.html
看到这里给个好东西hhh......文章来源地址https://www.toymoban.com/news/detail-776166.html
子问题的和: dfs(x) = dfs(x + 1) + dfs(x + 2);最优子问题: dfs(x) = max(dfs(x + 1),dfs(x + 2));到了这里,关于动态规划(DP)---- 01背包入门详解----二维图是学会的关键的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!