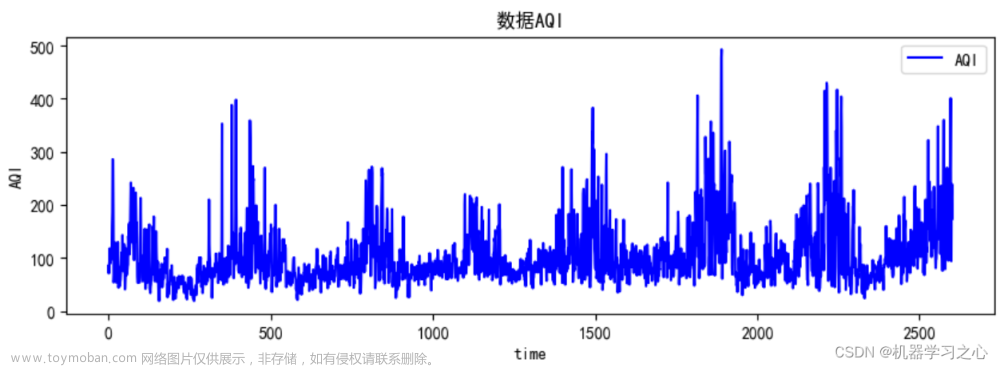
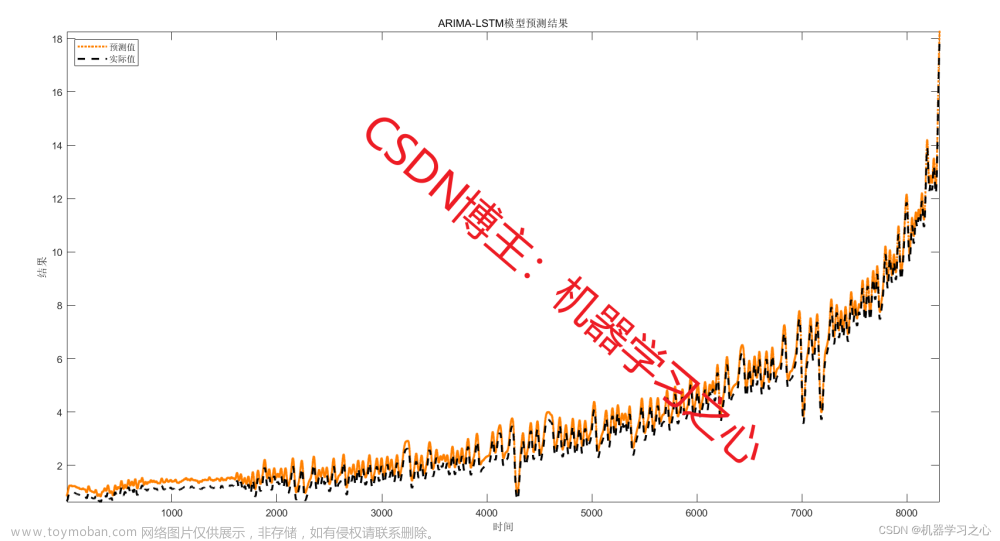
一、理论知识
基本思想:
ARIMA模型的全称叫做自回归移动平均模型,全称是(ARIMA,Autoregressive Integrated Moving Average Model)。也记作ARIMA(p,d,q),是统计模型(statisticmodel)中最常见的一种用来进行时间序列预测的模型。
基本原理:
将非平稳时间序列转化为平稳时间序列然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。
ARIMA模型本质上由三部分组成,AR(p阶自回归模型)+I(i阶差分)+MA(q阶移动平均模型)。
基本步骤:
1)导入实验数据。2)确定ARMA模型阶数。3)残差检验。4)给出结果
优点:
一般用ARMA模型拟合时间序列,预测该时间序列未来值。Daniel检验平稳性。自动回归AR(Autoregressive)和 移动平均MA(Moving Average)预测模型,预测精度相对较高,适合中长期预测问题
缺点:
当遇到外界发生较大变化,往往会有较大偏差,时间序列预测法对于中短期预测的效果要比长期预测的效果好。
应用范围:
根据客观事物发展的这种连续规律性,运用过去的历史数据,通过统计分析,进一步推测市场未来的发展趋势。时间序列,在时间序列分析预测法处于核心位置
二、ARIMA建模流程总结:
1、收集数据(并补全缺失值)
如果有缺失数据,按照下面步骤(一般使用“序列均值”进行补全)


2、时序图和检验平稳性
首先,定义好日期:


此时会新生成一列数据,如下

然后创建时间序列:
方法一:


方法二:
分析->预测->序列图

先看一看原始序列是什么样子:


显然这个数据是非平稳的(可以暂且认为他是存在一定的季节性波动)
3、对非平稳序列进行平稳化处理,差分次数d的确定,根据差分次数d,建立差分序列
我们可以试一下季节性差分:


虽然效果比初始好了一些,但是我们能看到他仍然是有一个上升趋势的,还是非平稳的


这么看来这个基本上已经平稳了
4、模型识别和定阶,p阶和q阶确定:ACF和PACF
画一下自相关图



可以看到他也是不平稳的,进行平稳化处理:



5、模型的参数估计







6、模型的适应性检验
原始数据无任何处理的分析

这里R方是926比较高,说明拟合效果比较好
显著性小于0.05说明这个模型的序列可能存在一定的自相关问题



可以看到拟合的效果也是可以的文章来源:https://www.toymoban.com/news/detail-776273.html
原始数据进行平方根处理之后分析
我们来看一看原始数据进行平方根处理之后效果会不会更好一些:文章来源地址https://www.toymoban.com/news/detail-776273.html





7、利用ARIMA(p,d,q)模型进行预测

到了这里,关于时间序列ARIMA模型的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!