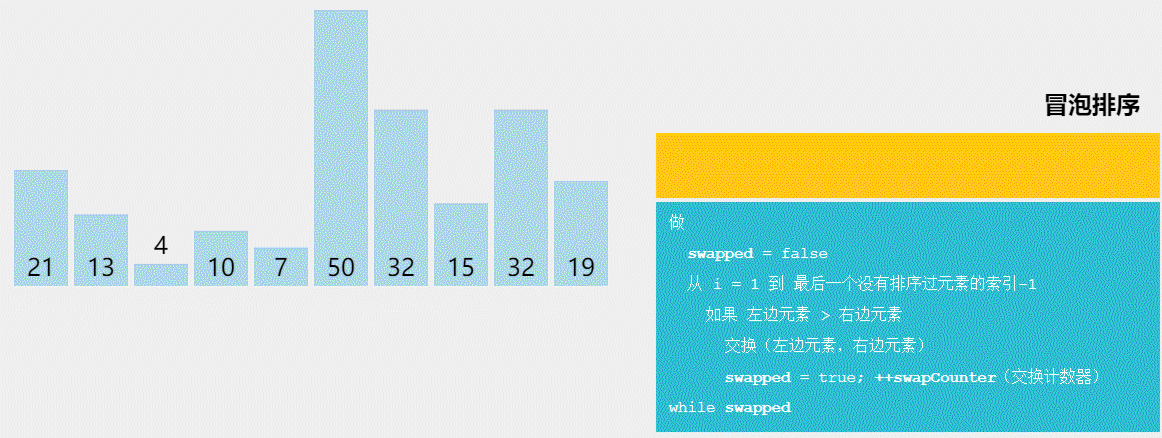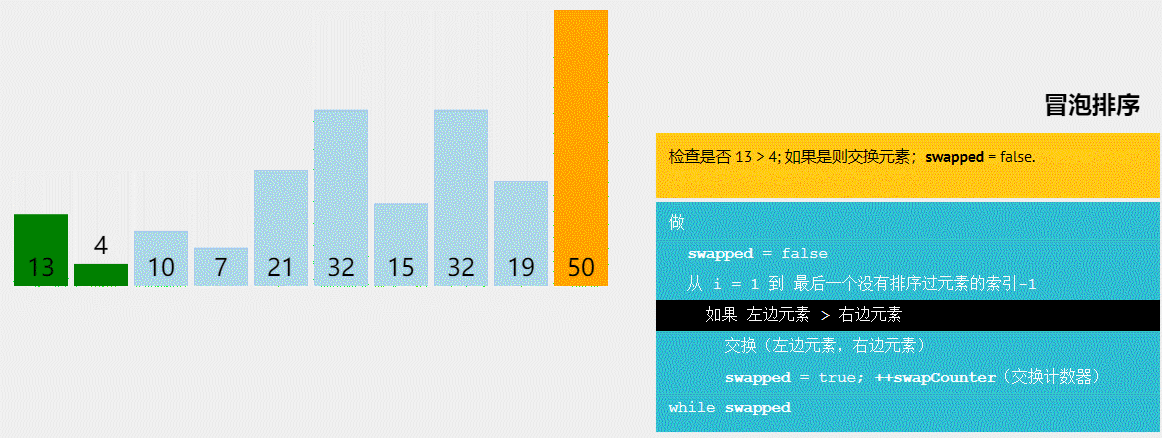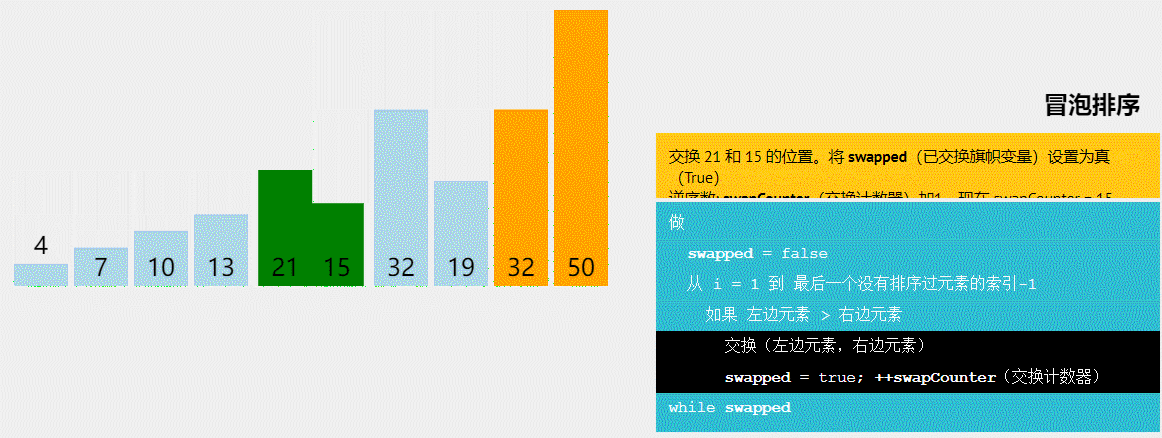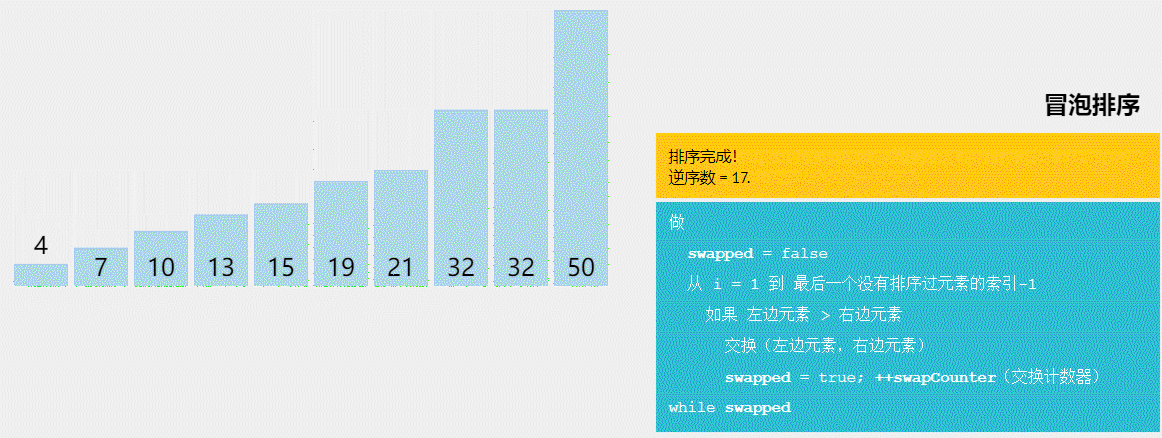目录
1、插入排序
思路
实现
2、希尔排序
思路
实现
3、选择排序
思路
实现
4、堆排序
思路
实现
5、冒泡排序
思路
实现
6、快速排序
方法一：霍尔快排法
方法二：挖坑法
方法三：前后指针法
7、归并排序
思路
实现
1、插入排序
思路
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中，直到所有的记录插入完为止，得到一个新的有序序列
直接插入排序的特性总结：
1. 元素集合越接近有序，直接插入排序算法的时间效率越高
2. 时间复杂度：O(N^2)
3. 空间复杂度：O(1)，它是一种稳定的排序算法
4. 稳定性：稳定
实现
//插入排序 void InsertSort(int* a, int n) { for (int i = 0; i < n - 1; ++i) { // [0, end] 有序，插入tmp依旧有序 int end = i; int tmp = a[i + 1]; while (end >= 0) { if (a[end] > tmp) { a[end + 1] = a[end]; --end; } else { break; } } a[end + 1] = tmp; } }
2、希尔排序
思路
希尔排序法又称缩小增量法。
1、预排序 --->接近有序
2、直接插入排序
希尔排序法的基本思想是：
1、先选定一个整数gap，把待排序文件中所有记录分成gap个组，
2、所有距离为gap的记录分在同一组内，并对每一组内的记录进行排序。
3、然后重复上述分组和排序的工作。当到达gap = 1时，所有记录在统一组内排好序。
gap越大，大的数可以更快的到后面，小的数可以更快的到前，越不接近有序
gap越小，大的小的挪动越慢，但是他越接近有序
gap == 1，就是直接插入排序
希尔排序的特性总结：
1. 希尔排序是对直接插入排序的优化。
2. 当gap > 1时都是预排序，目的是让数组更接近于有序。当gap == 1时，数组已经有序了，这样就会很快。这样整体而言，可以达到优化的效果。
3. 希尔排序的时间复杂度不好计算，因为gap的取值方法很多，导致很难去计算，因此在好些树中给出的希尔排序的时间复杂度都不固定。
4. 稳定性：不稳定
实现
void ShellSort(int* a, int n) { // 1、gap > 1 预排序 // 2、gap == 1 直接插入排序 int gap = n; while (gap > 1) { gap = gap / 3 + 1; // +1可以保证最后一次一定是1 // gap = gap / 2; for (int i = 0; i < n - gap; ++i) { int end = i; int tmp = a[end + gap]; while (end >= 0) { if (a[end] > tmp) { a[end + gap] = a[end]; end -= gap; } else { break; } } a[end + gap] = tmp; } } }
3、选择排序
思路
每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完
直接选择排序的特性总结：
1. 直接选择排序思考非常好理解，但是效率不是很好。实际中很少使用
2. 时间复杂度：O(N^2)
3. 空间复杂度：O(1)
4. 稳定性：不稳定
实现
void Swap(int* p1, int* p2) { int tmp = *p1; *p1 = *p2; *p2 = tmp; } void SelectSort(int* a, int n) { int begin = 0, end = n - 1; while (begin < end) { //找出最大和最小值放在开头和结尾，然后begin++，end-- int maxi = begin, mini = begin; for (int i = begin; i <= end; i++) { if (a[i] > a[maxi]) { maxi = i; } if (a[i] < a[mini]) { mini = i; } } Swap(&a[begin], &a[mini]); // 如果maxi和begin重叠，修正一下即可 //如果maxi和begin重叠，可能会重复交换 if (begin == maxi) { maxi = mini; } Swap(&a[end], &a[maxi]); ++begin; --end; } }
4、堆排序
思路
堆排序 是指利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆，排降序建小堆。不知道堆的可以参考： 数据结构：堆的实现_元清加油的博客-CSDN博客
堆排序的特性总结：
1. 堆排序使用堆来选数，效率就高了很多。
2. 时间复杂度：O(N*logN)
3. 空间复杂度：O(1)
4. 稳定性：不稳定
实现
//向下调整法（排升序，建大堆） void AdjustDown1(int* a, int n, int parent) { int child = parent * 2 + 1; while (child < n) { // 找出小的那个孩子 if (child + 1 < n && a[child + 1] > a[child]) { ++child; } if (a[child] > a[parent]) { Swap(&a[child], &a[parent]); parent = child; child = parent * 2 + 1; } else { break; } } } //向下调整法（排降序，建小堆） void AdjustDown2(int* a, int n, int parent) { int child = parent * 2 + 1; while (child < n) { // 找出大的那个孩子 if (child + 1 < n && a[child + 1] < a[child]) { ++child; } if (a[child] < a[parent]) { Swap(&a[child], &a[parent]); parent = child; child = parent * 2 + 1; } else { break; } } } void HeapSort(int* a, int n) { // 排升序，建大堆 for (int i = (n - 1 - 1) / 2; i >= 0; --i) { AdjustDown1(a, n, i); } // 排降序，建小堆 for (int i = (n - 1 - 1) / 2; i >= 0; --i) { AdjustDown2(a, n, i); } //堆删除的思想 int end = n - 1; while (end > 0) { Swap(&a[0], &a[end]); AdjustDown(a, end, 0); --end; } }
5、冒泡排序
思路
冒泡排序非常的简单，相邻二个数比较大小，然后交换即可
冒泡排序的特性总结：
1. 冒泡排序是一种非常容易理解的排序
2. 时间复杂度：O(N^2)
3. 空间复杂度：O(1)
4. 稳定性：稳定
实现
void BubbleSort(int* a, int n) { for (int j = 0; j < n; ++j) { bool exchange = false; for (int i = 1; i < n - j; i++) { if (a[i - 1] > a[i]) { int tmp = a[i]; a[i] = a[i - 1]; a[i - 1] = tmp; exchange = true; } } if (exchange == false) { break; } } }
6、快速排序
快速排序的特性总结：
1. 快速排序整体的综合性能和使用场景都是比较好的，所以才敢叫快速排序
2. 时间复杂度：O(N*logN)
3. 空间复杂度：O(logN)
4. 稳定性：不稳定
方法一：霍尔快排法
思路
取第一个数为key，从左右出发，右边找小于key的数，左边找大于key的数，找到交换。直到左边大于右边，就交换key和左边的数
实现
void Swap(int* str1, int* str2) { int temp = *str1; *str1 = *str2; *str2 = temp; } int PartSort1(int* a, int left, int right) { int keyi = left; while (left < right) { // 右边找小 while (left < right && a[right] >= a[keyi]) { --right; } // 左边找大 while (left < right && a[left] <= a[keyi]) { ++left; } Swap(&a[left], &a[right]); } Swap(&a[keyi], &a[left]); return left; } void QuickSort(int* a, int begin, int end) { if (begin >= end) return; int keyi = PartSort2(a, begin, end); // [begin, keyi-1] keyi [keyi+1, end] QuickSort(a, begin, keyi - 1); QuickSort(a, keyi + 1, end); } int main() { int arr[] = { 6,1,2,7,9,3,4,5,10,8 }; QuickSort(arr, 0, 9); for (int i = 0; i < 9; i++) { printf("%d ", arr[i]); } return 0; }
方法二：挖坑法
思路
取第一个数为key，从左右出发，右边找小于key的数，把他设立为一个坑位，左边找大于key的数，把他设立为一个新的坑位。直到左边大于右边，就交换key和坑的数
实现
// 挖坑法 // [left, right] int PartSort2(int* a, int left, int right) { int key = a[left]; int hole = left; while (left < right) { // 右边找小 while (left < right && a[right] >= key) { --right; } a[hole] = a[right]; hole = right; // 左边找大 while (left < right && a[left] <= key) { ++left; } a[hole] = a[left]; hole = left; } a[hole] = key; return hole; } void QuickSort(int* a, int begin, int end) { if (begin >= end) return; int keyi = PartSort2(a, begin, end); // [begin, keyi-1] keyi [keyi+1, end] QuickSort(a, begin, keyi - 1); QuickSort(a, keyi + 1, end); } int main() { int arr[] = { 6,1,2,7,9,3,4,5,10,8 }; QuickSort(arr, 0, 9); for (int i = 0; i < 9; i++) { printf("%d ", arr[i]); } return 0; }
方法三：前后指针法
思路
取第一个数为key，初始时，prev指针指向序列开头，cur指针指向prev后一个位置。cur找小与key的数与（prev++）交换
实现
// 前后指针法 // [left, right] int PartSort3(int* a, int left, int right) { int prev = left; int cur = left + 1; int keyi = left; while (cur <= right) { if (a[cur] < a[keyi] && ++prev != cur) { Swap(&a[prev], &a[cur]); } ++cur; } Swap(&a[prev], &a[keyi]); keyi = prev; return keyi; } void QuickSort(int* a, int begin, int end) { if (begin >= end) return; int keyi = PartSort2(a, begin, end); // [begin, keyi-1] keyi [keyi+1, end] QuickSort(a, begin, keyi - 1); QuickSort(a, keyi + 1, end); } int main() { int arr[] = { 6,1,2,7,9,3,4,5,10,8 }; QuickSort(arr, 0, 9); for (int i = 0; i < 9; i++) { printf("%d ", arr[i]); } return 0; }
7、归并排序
思路
归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用 分治法（Divide andConquer） 的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并
文章来源：https://www.toymoban.com/news/detail-776309.html
归并排序的特性总结：
1. 归并的缺点在于需要O(N)的空间复杂度，归并排序的思考更多的是解决在磁盘中的外排序问题
2. 时间复杂度：O(N*logN)
3. 空间复杂度：O(N)
4. 稳定性：稳定
实现
//归并排序 void _MergeSort(int* a, int begin, int end, int* tmp) { if (begin == end) return; int mid = (begin + end) / 2; // [begin, mid] [mid+1, end] _MergeSort(a, begin, mid, tmp); _MergeSort(a, mid + 1, end, tmp); // 归并两个区间 // ... int begin1 = begin, end1 = mid; int begin2 = mid + 1, end2 = end; int i = begin; while (begin1 <= end1 && begin2 <= end2) { if (a[begin1] <= a[begin2]) { tmp[i++] = a[begin1++]; } else { tmp[i++] = a[begin2++]; } } while (begin1 <= end1) { tmp[i++] = a[begin1++]; } while (begin2 <= end2) { tmp[i++] = a[begin2++]; } memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1)); } void MergeSort(int* a, int n) { int* tmp = (int*)malloc(sizeof(int) * n); _MergeSort(a, 0, n - 1, tmp); free(tmp); }
文章来源地址https://www.toymoban.com/news/detail-776309.html
到了这里，关于史上最全的排序讲解的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
