[动态规划] 01背包问题及其优化-Toy模板网

这篇具有很好参考价值的文章主要介绍了[动态规划] 01背包问题及其优化。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

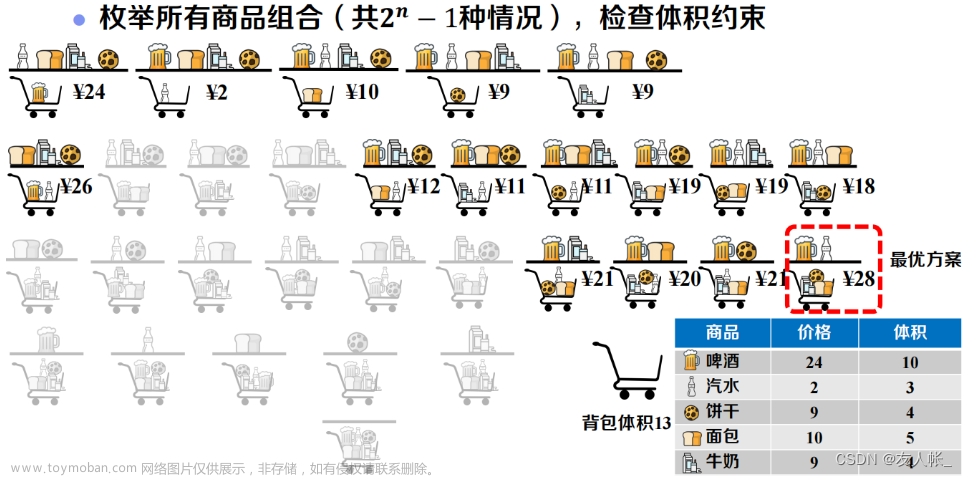
题目描述

给一个能承重V的背包，和n件物品，我们用重量和价值的二元组来表示一个物品，第i件物品表示为（Vi，Wi），问：在背包不超重的情况下，得到物品的最大价值是多少？

[动态规划] 01背包问题及其优化,动态规划,算法

输入

第一行输入两个数 V,n，分别代表背包的最大承重和物品数。

接下来n行，每行两个数Vi,Wi，分别代表第i件物品的重量和价值。

(Vi≤V≤10000,n≤100,Wi≤1000000)

输出

输出一个整数，代表在背包不超重情况下所装物品的最大价值。

样例输入1

样例输出1

数据规模与约定

时间限制：1 s

内存限制：64 M

100% 的数据保证(Vi≤V≤10000,n≤100,Wi≤1000000)

解题分析1

采用容斥原理，首先，采用二维dp数组即dp[i][j]，其中i表示前i个物品，j表示背包的容量，考虑递推关系，对于第i个物品，我们有两种办法，取或不取，如果取，那么我们得到了dp[i][j]=dp[i-1][j-w[i]]+v[i]，即我们取前i个物品，背包容量为j的情况下能得到的物品价值，当然，我们也可以不取，则我们得到dp[i][j]=dp[i-1][j]，即我们不用消耗背包容量w[i]，直接以j的容量去取前i-1个物品，在实际的刷表过程中，我们还需要加一个判断条件，取的情况下，必须是当前背包容量j大于我们考虑的这个物品i的重量w[i]才行！这样，我们就完成了我们的第一个版本的01背包代码。

代码实现1

#include <iostream>
#define MAXN 10005
using namespace std;

int n,V,w[MAXN],v[MAXN];
int dp[MAXN][MAXN];

int main(){
	scanf("%d%d",&V,&n);
	for(int i=1;i<=n;i++){
		scanf("%d%d",&w[i],&v[i]);
	}
	for(int i=1;i<=n;i++)
		for(int j=1;j<=V;j++){
			dp[i][j]=dp[i-1][j];
			if(w[i]<=j)
				dp[i][j]=max(dp[i][j],dp[i-1][j-w[i]]+v[i]);
		}
	printf("%d\n",dp[n][V]);
	return 0;
}

解题分析2

接下来我们进一步地去优化这个代码看看吧！首先，我们观察递推关系，我们惊讶地发现，dp[i][j]的状态仅仅取决于dp[i-1][j-w[i]]和dp[i-1][j]的状态罢了！所以，我们完全没有必要开那么大的dp数组，纯粹属于浪费内存了，那我们怎么办呢？直接采用滚动数组，设置两个变量在0,1之间循环存储上一个状态下的内容，然后再去刷表即可，代码实现如下。

代码实现2

#include <iostream>
#define MAXN 10005
using namespace std;

int n,V,w[MAXN],v[MAXN];
int dp[2][MAXN],ind,rind;

int main(){
	scanf("%d%d",&V,&n);
	for(int i=1;i<=n;i++){
		scanf("%d%d",&w[i],&v[i]);
	}
	for(int i=1;i<=n;i++)
		for(int j=1;j<=V;j++){
			ind=i%2,rind=(i-1)%2;
			dp[ind][j]=dp[rind][j];
			if(w[i]<=j)
				dp[ind][j]=max(dp[ind][j],dp[rind][j-w[i]]+v[i]);
		}
	printf("%d\n",dp[n%2][V]);
	return 0;
}

解题分析3

实际上，我们可以发现代码还有进一步优化的空间，我们再仔细观察我们dp数组打表的过程，可以发现，我们每次就用到了w[i]和v[i]而已，完全没用到其他情况下的物品的重量和价值，所以，我们不用先读入每个物品的重量和价值，而是采用边读入边打表的方式，又剩下了一比空间的开销，而且时间上也更加优化。

代码实现3

#include <iostream>
#define MAXN 10005
using namespace std;

int n,V,w,v;
int dp[2][MAXN],ind,rind;

int main(){
	scanf("%d%d",&V,&n);
	for(int i=1;i<=n;i++){
		scanf("%d%d",&w,&v);
		for(int j=1;j<=V;j++){
			ind=i%2,rind=(i-1)%2;
			dp[ind][j]=dp[rind][j];
			if(w<=j)
				dp[ind][j]=max(dp[ind][j],dp[rind][j-w]+v);
		}
	}
	printf("%d\n",dp[n%2][V]);
	return 0;
}

解题分析4

实际上本题还可以进行终极优化，形成一个最最简单的01背包代码，注意到，我们每次都是考虑三个状态,dp[i][j],dp[i-1][j],dp[i-1][j-w[i]]+v[i]，这些状态只是和上一次状态有关而已，所以我们只需要一个一维数组来帮助我们打表即可，我们在第一次刷表的时候，相当于就是对第一个物品dp[1][w]，w在1到V进行打表，而后，我们只需要反向地进行打表即可，这个时候我们确保j是大于当前物品v[i]的，因为没更新的一维数组相当于上一次的i-1的数据，当j小于v[i]的时候，我们都取i-1的数据，所以不能对那个地方进行打表。反向打表还有一个好处就是，符合了我们此时的逻辑，因为前面的数据都是没有更新过的，没有更新过的数据就都是上一次i-1的，这样就不用开两个数组了。文章来源地址https://www.toymoban.com/news/detail-776453.html

代码实现4

#include <iostream>
#define MAXN 10005
using namespace std;

int n,V,dp[MAXN];

int main(){
	scanf("%d%d",&V,&n);
	for(int i=1,w,v ;i<=n ; i++){
		scanf("%d%d",&w,&v);
		for(int j=V ; j>=w ; j--){
			dp[j]=max(dp[j],dp[j-w]+v);
		}
	}
	printf("%d\n",dp[V]);
	return 0;
}

到了这里，关于[动态规划] 01背包问题及其优化的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！